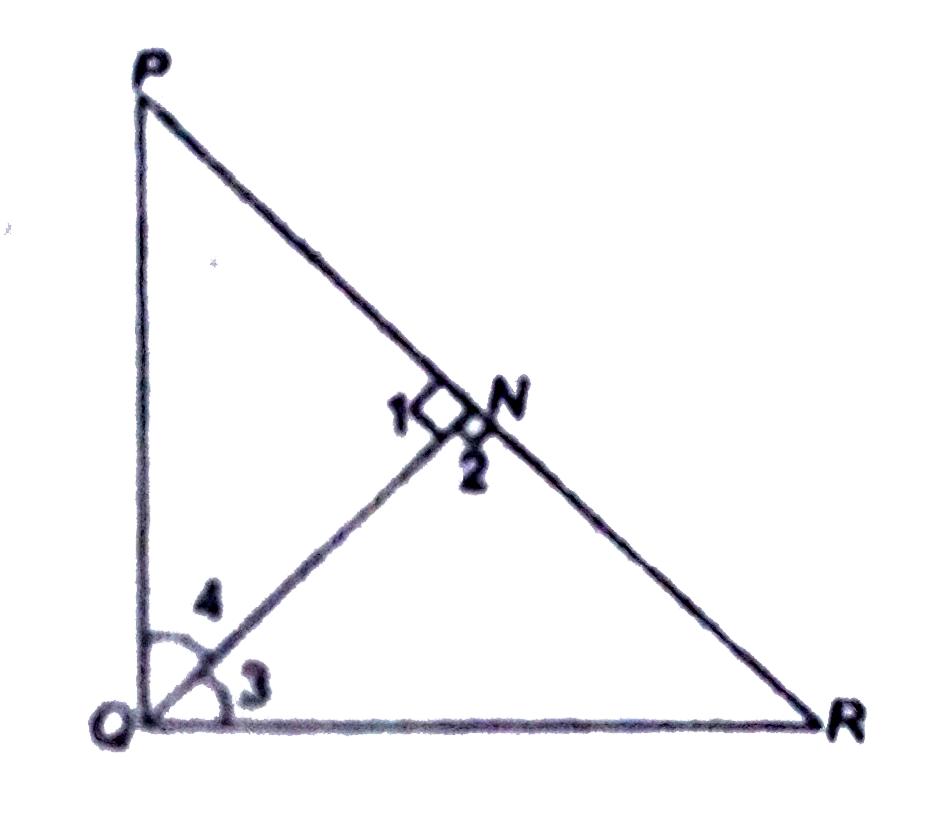
In a ΔPQR, N is a point on PR, such that QN⊥PR. If PN⋅NR=QN2, then prove that ∠PQR=90∘.
Given : △PQR in which QN⊥PRandPN×NR=QN2
To prove , ∠PQR=90∘
Proof : In △QNPand△QNR
QN⊥PR
∠2=∠1=90∘
QN2=NR×NP
QNNR=NPQNorQNNP=NRQN
△QNR~△PNQ ( by SAS similarity criterion)
∠3=∠P ..(1)
∠2=∠1=90∘
∠R=∠4 ...(2)
In △PQR we have
∠P+∠PQR+∠R=180∘ ( angle sum property of a trangle)
∠3+∠4+∠3+∠4=180∘ [ using (1) and (2) ]
⇒ 2∠3+2∠4=180∘
⇒ ∠3+∠4=90∘
∠PQR=90∘ Hence proved
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Eercise 6b
1 Video
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
1 Video
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In a triangle ABC , N is a point on AC such that BN⊥AC . If BN2=ANNC , prove that ∠B=90o .
View SolutionIf Q is a point on the side SR of a triangle ΔPSR such that PQ=PR then prove that PS>PQ
View SolutionIi ΔPQR, PD⊥QR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=d, then prove that (a+b)(a-b)=(c+d)(c-d).
View SolutionIn ΔPQR,PQ=PR.A is a point in PQ and B is a point in PR , so that
QR = RA = AB = BP
show that :∠P:∠R=1:3
View SolutionIn ΔPQR,PQ=PR.A is a point in PQ and B is a point in PR , so that
QR = RA = AB = BP
Find the vlaue of ∠Q.
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
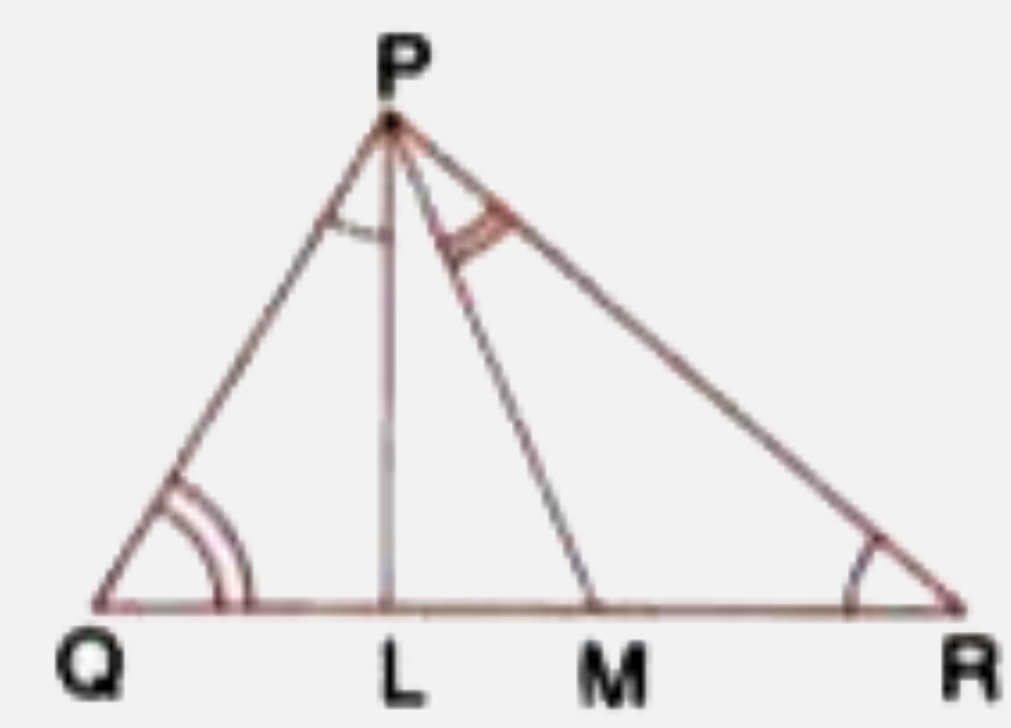
ΔPQL~ΔRPM
View SolutionThe sides PQ, PR of triangle PQR are equal, and S, T are points on PR, PQ such that ∠PSQand∠PTR are right angles
Prove that the triangles PTR and PSQ are congruent.
View SolutionA Δ ABC is right angled at A. L is a point on BC such that AL⊥ BC. Prove that ∠BAL=∠ACB.
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
View SolutionA ΔABC is right angled at A. L is a point on BC such that AL⊥ BC. Prove that ∠BAL=∠ACB.
View Solution
