In figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
In figure AB||PQ (given )
⇒ OAAP=OBBQ
( basic proportonality theorem) ….(1)
Also in figure AC||PR (given)
⇒ OAAP=OCCR ( basic proportionality theorem) …. (2)
from equatlons ( 1) and (2) , we get
OBBQ=OCCR
BC||QR ( converse of basic proportionality theorem)

Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Eercise 6b
1 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
1 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.

View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PQ = QR
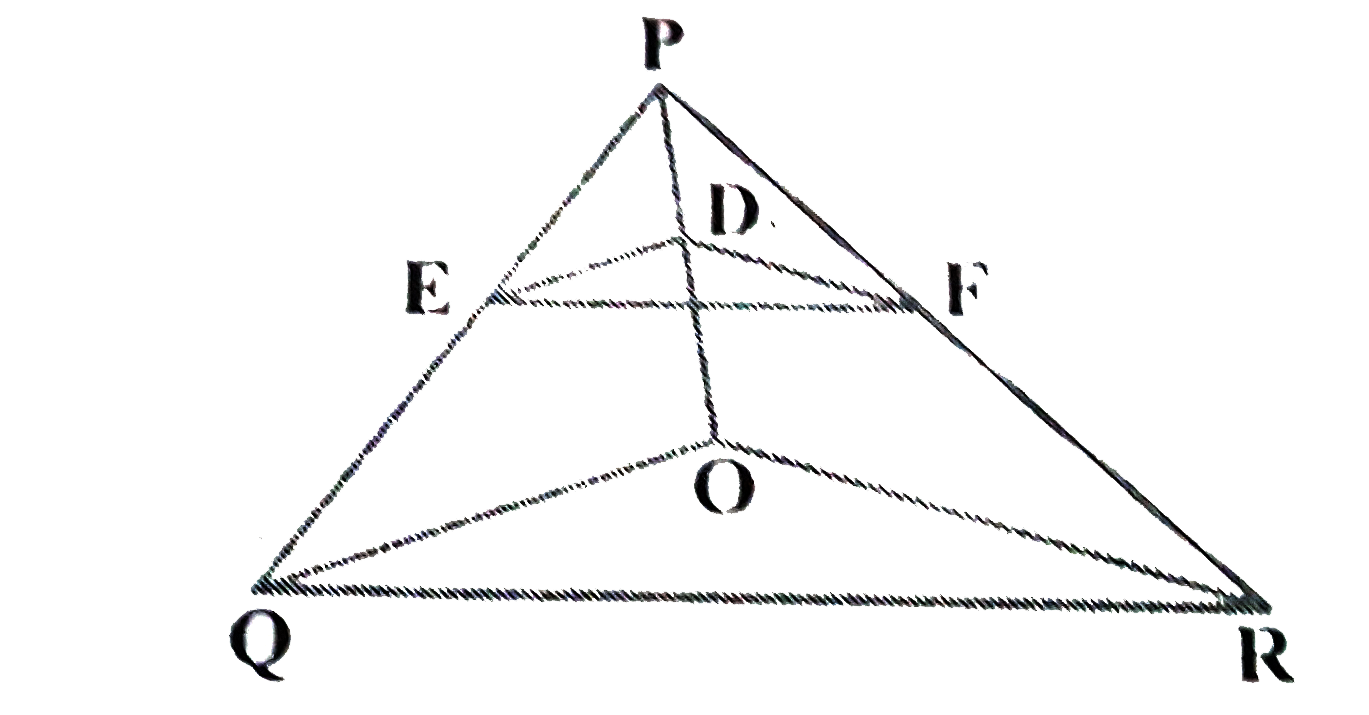
View SolutionIn figure DE || OQ and DF || OR. Show that EF||QR.
View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points on the sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View Solution□PQRS is a reactangle. If A, B and C are the mid-points of PQ, PS and QR respectively, then prove that
AB+AC=12(PR+SQ).
View SolutionIn three line segments OA,OBandOC, point L,M,N respectively are so chosen that LM||ABandMN||BC but neither of L,M,N nor of A,B,C are collinear. Show that LN∣∣AC.
View SolutionIn the figure, given below X and Y are the mid-points of AB and AC respectively. Given that BC = 6 cm, AB = 5-4 cm and AC = 5-0 cm, calculate the perimeter of trapezium YXBC.

View SolutionLet ABC be a triangle and DandE be two points on side AB such that AD=BE. If DP∣∣BC and EQ∣∣AC, Then prove that PQ∣∣AB.
View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD and FE bisect each other.
View SolutionIn triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
View Solution
