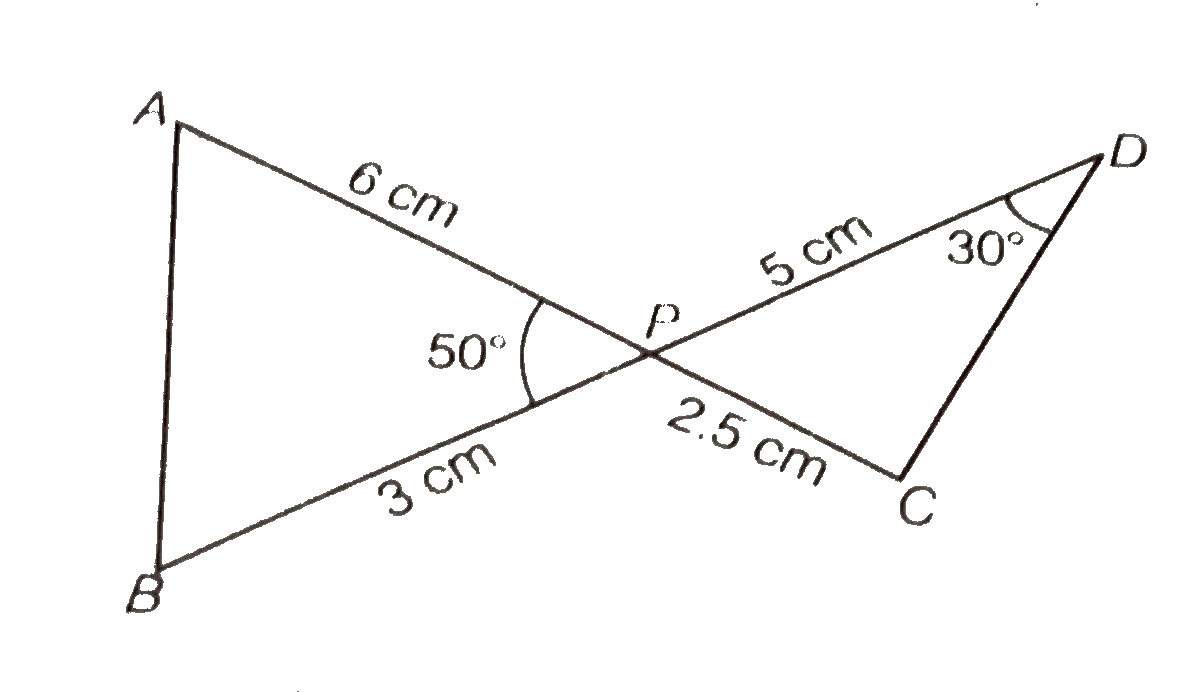
In figure, two line segments AC and BD intersects each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD=5 cm, ∠APB=50∘ and ∠CDP=30∘. Then, ∠PBA is equal to
50∘
30∘
60∘
100∘
The correct Answer is:D
In ΔAPBandΔCPD∠APB=∠CPD=50∘ [vertically opposite angle]
APPD=65….(i)
and BPCP=32.5=65….(ii)
From Eqs. (i) and (ii)
APPD=BPCP
∴ΔAPB~ΔDPC [by SAS similarity critrion]
∴∠A=∠D=30∘[corresponding angles of similar triangles]
In ΔAPB,∠A+∠B+∠APB=180∘ [sum of angles of a triangle=180∘]
⇒30∘+∠B+50∘=180∘
∴∠B=180∘−(50∘+30∘)=100∘
i.e., ∠PBA=100∘
Topper's Solved these Questions
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:Very Short Answer Typw Questions
Explore 12 Videos
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:Short Answer Type Questions
Explore 15 Videos
- SURFACE AREAS AND VOLUMESBook:NCERT EXEMPLAR ENGLISHChapter:SURFACE AREAS AND VOLUMESExercise:LONG ANSWER TYPE QUESTIONS
Explore 20 Videos
Similar Questions
In a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
PA×PD=PB×PC.
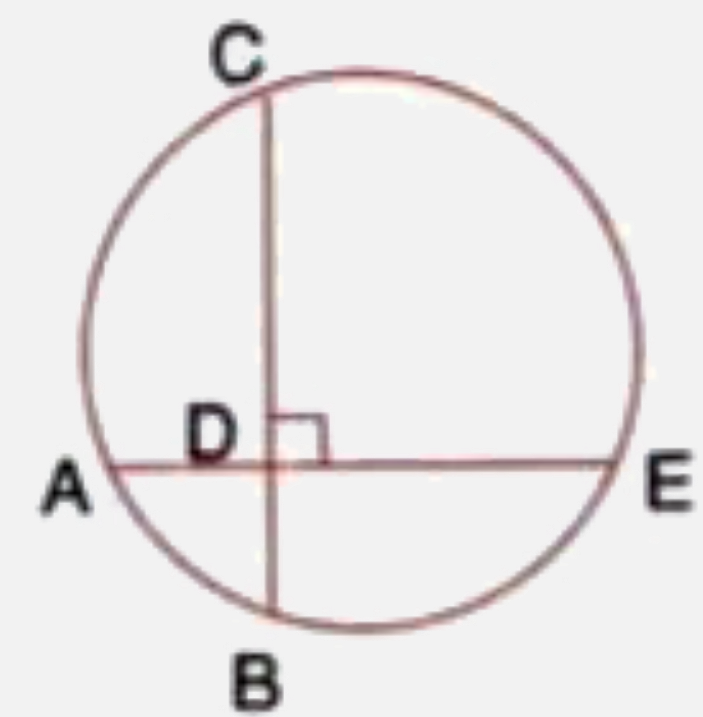
View SolutionIn the given figure, AE and BC intersect each other at point D.
If ∠CDE=90∘,AB=5cm,BD=4 and CD=9 find AE
View SolutionConstruct a quadrilateral in which AB=5.4cm,BC=2.5cm,CD=4cm,AC=6.5cmandBD=5cm
View SolutionDraw a line segment of length 5.3cms
View SolutionIn the figure, given below, straight lines AB and CD intersect at P, and AC//BD.

If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm, find the lengths of PA and PC.
View SolutionConstruct a ΔABC with sides AB = 6 cm, BC = 5.2 cm and AC = 4.6 cm.
View SolutionDraw a line segment AB=5.5 cm. mark a point P, such that PA=6cm and PB=4.8 cm. from the point P, draw a perpendicular to AB.
View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PA= 8cm, PC= 5cm and PD= 4cm, determine AB.
View SolutionConstruct a rhombus ABCD in which
AC = 5.6 cm and BD = 6.3 cm
View SolutionIn the figure chords AE and BC intersect each other at point D
(i) If ∠CDE=90∘
AB=5cm
BD=4cm and CD=9 cm
find DE
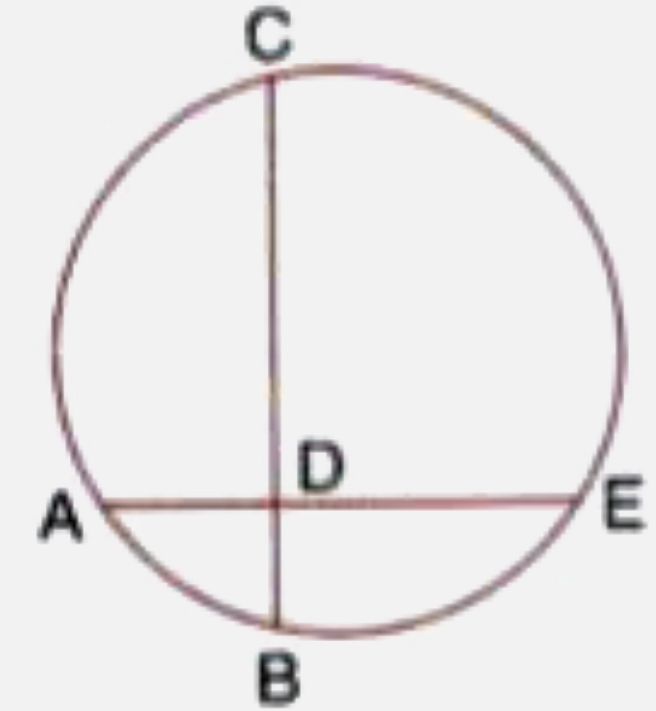
(ii) If AD=BD, show that AE=BC
View Solution

