A mass M is supported by a massless string wound round a uniform cylinder ofmass M and radius R. On releasing the mass from rest, it will fall with acceleration?

(a)g
(b)g/2
(c)g/3
(d)2g/3
The correct Answer is:D
Mgh=12Mv2+12Iω2 =12Mv2+12[12MR2]ω2=12Mv2+14Mv2=34Mv2 v=√2ah∵Mgh=34M×2aha=23g. Solve by force /torque and Newton.s law also.
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-1
4 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-2
5 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
Similar Questions
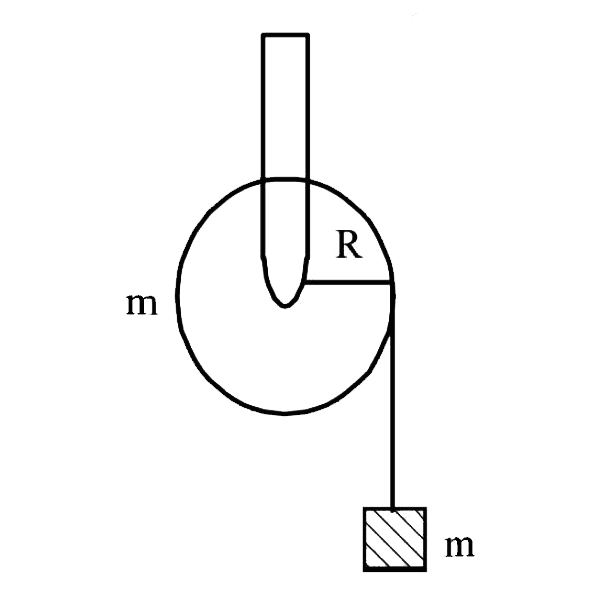
A mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
View SolutionA load of mass m is attached to the end of a string wound on a cylinder of mass M and radius R. The string passes round a pulley.
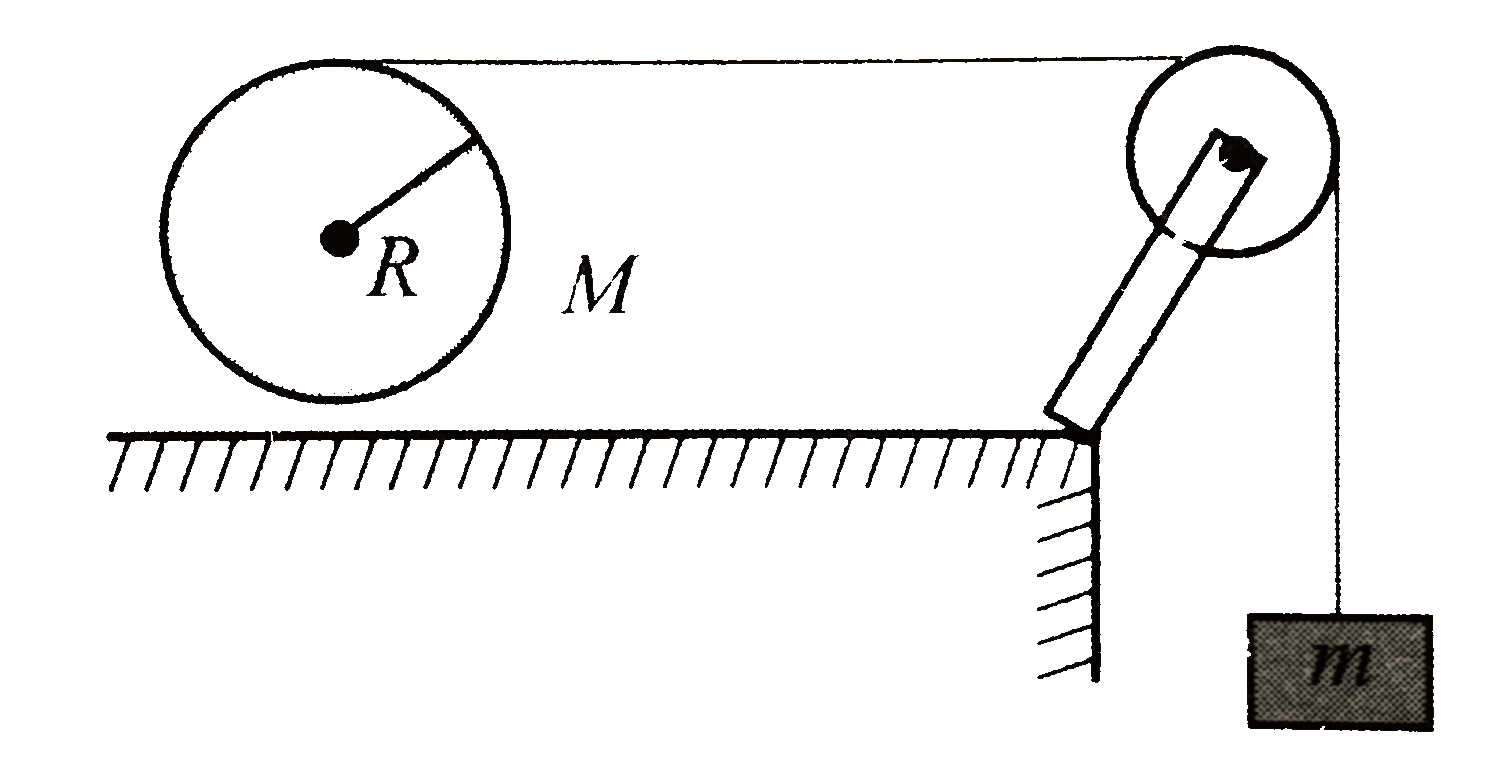
a. Find the acceleration of the cylinder M when it rolls.
b. If the coefficient of friction is μ. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls always
View SolutionAs shown in the figure, a bob of mass m is tied by a massless string whose other end is wound on a fly wheel Ring of radius r and mass m. When released from rest the bob starts falling vertically. When it has covered a distance of h, the speed of the bob will be :
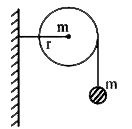
View SolutionAs shown in the figure, a bob of mass m is tied by a massless string whose other end is wound on a fly wheel Ring of radius r and mass m. When released from rest the bob starts falling vertically. When it has covered a distance of h, the speed of the bob will be :
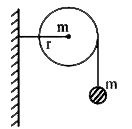
View SolutionAs shown in the figure, two bobs of masses m & 2m are tied by a massless string which is wound on a fly wheel (disc) of radius r and mass m. When released from rest the bob of mass 2m starts falling vertically. When it has covered distance of h, the angular speed of the wheel will be:
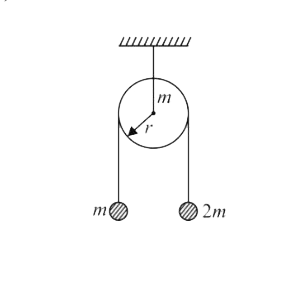
View SolutionAs shown in the figure, two bobs of masses m & 2m are tied by a massless string which is wound on a fly wheel (disc) of radius r and mass m. When released from rest the bob of mass 2m starts falling vertically. When it has covered distance of h, the angular speed of the wheel will be:

View SolutionAs shown in fig., a bob of mass m is tied by a massless string whose other end portion is wound on a fly wheel (disc) of radius r and mass 2m. when released from rest the bob starts falling vertically. The time taken by the bob to descend through a height h, from the initial position, is
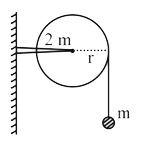
View SolutionAs shown in fig., a bob of mass m is tied by a massless string whose other end portion is wound on a fly wheel (disc) of radius r and mass 2m. when released from rest the bob starts falling vertically. The time taken by the bob to descend through a height h, from the initial position, is

View SolutionOne end of a massless string is wound around a cylinder of mass 5 kg and radius 16' cm. The cylinder' is mounted symmetrically on a horizontal axle so 5 that It can freely rotate about its axis, to the other end of the string a mass of 500 gm is attached. Calculate the acceleration of the mass when it is released from rest.
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View Solution
