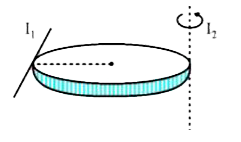
If the moment of inertia of a disc about an axis tangential and parallel to its surface be I, then what will be the moment of inertia about the axis tangential but perpendicular to the surface?
65I
34I
32I
54I
The correct Answer is:A
I1=(14mr2)+mr2=5mr24=I ⇒I2=12mr2+mr2=32mr2=6I5
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-1
4 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-2
5 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
Similar Questions
Knowledge Check
If the moment of inertion of a disc about an axis tangentially and parallel to its surface by I, then what will be the moment of inertia about the axis tangential but perpendicular to the surface
A65IB34IC32ID54I
Calculate the moment of inertia of a disc about its any diameter ?
View SolutionThe moment of inertia of a body about a given axis of rotation depends upon :-
View SolutionThe moment of inertia of ring about an axis passing through its diameter is I. Then moment of inertia of that ring about an axis passing through its centre and perpendicular to its plane is
View SolutionWhat is the moment of inertia of a circular disc about one of its diameters ?
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View SolutionCalculate the moment of inertia of the given rod about an axis CD.
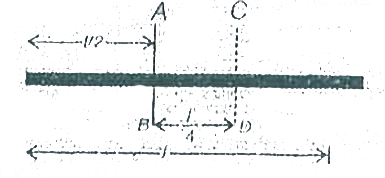
View SolutionA circular disc of radius R and thickness R6 has moment of inertia I about its axis. If it is melted and casted into a solid sphere then what will be its moment of inertia, about its diametric axis?
View Solution
