A disc rolls over a horizontal floor without slipping with a linear speed of 5 cm/sec. Then the linear speed of a particle on its rim, with respect to the floor, when it is in its highest position is?
10cm/sec
5cm/sec
2.5cm/sec
0
The correct Answer is:A
To solve the problem, we need to determine the linear speed of a particle on the rim of a disc when it is at its highest position, given that the disc rolls without slipping with a linear speed of 5 cm/sec.
1. Understand the Motion of the Disc:
- The disc rolls on a horizontal surface without slipping. This means that the point of contact with the ground (let's call it point A) is momentarily at rest.
2. Identify the Linear Speed:
- The linear speed (V) of the center of the disc is given as 5 cm/sec.
3. Relate Linear Speed to Angular Speed:
- For a disc rolling without slipping, the relationship between linear speed (V) and angular speed (ω) is given by:
V=ωR
- Here, R is the radius of the disc.
4. Determine the Speed at the Highest Point:
- The highest point of the disc (let's call it point C) will have two components of velocity:
- The linear speed of the center of the disc (V) acting forward.
- The tangential speed due to rotation (ωR), which is also acting forward at the highest point.
- Since the disc rolls without slipping, at the highest point, the total speed (V_C) can be expressed as:
VC=V+ωR
- Since V=ωR, we can substitute this into the equation:
VC=V+V=2V
5. Calculate the Speed at the Highest Point:
- Now substituting the value of V:
VC=2×5 cm/sec=10 cm/sec
6. Conclusion:
- The linear speed of the particle on the rim at its highest position with respect to the floor is 10 cm/sec.
- The disc rolls on a horizontal surface without slipping. This means that the point of contact with the ground (let's call it point A) is momentarily at rest.
- The linear speed (V) of the center of the disc is given as 5 cm/sec.
- For a disc rolling without slipping, the relationship between linear speed (V) and angular speed (ω) is given by:
V=ωR
- Here, R is the radius of the disc.
- The highest point of the disc (let's call it point C) will have two components of velocity:
- The linear speed of the center of the disc (V) acting forward.
- The tangential speed due to rotation (ωR), which is also acting forward at the highest point.
- Since the disc rolls without slipping, at the highest point, the total speed (V_C) can be expressed as:
VC=V+ωR
- Since V=ωR, we can substitute this into the equation:
VC=V+V=2V
- Now substituting the value of V:
VC=2×5 cm/sec=10 cm/sec
- The linear speed of the particle on the rim at its highest position with respect to the floor is 10 cm/sec.
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-1
4 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-2
5 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
Similar Questions
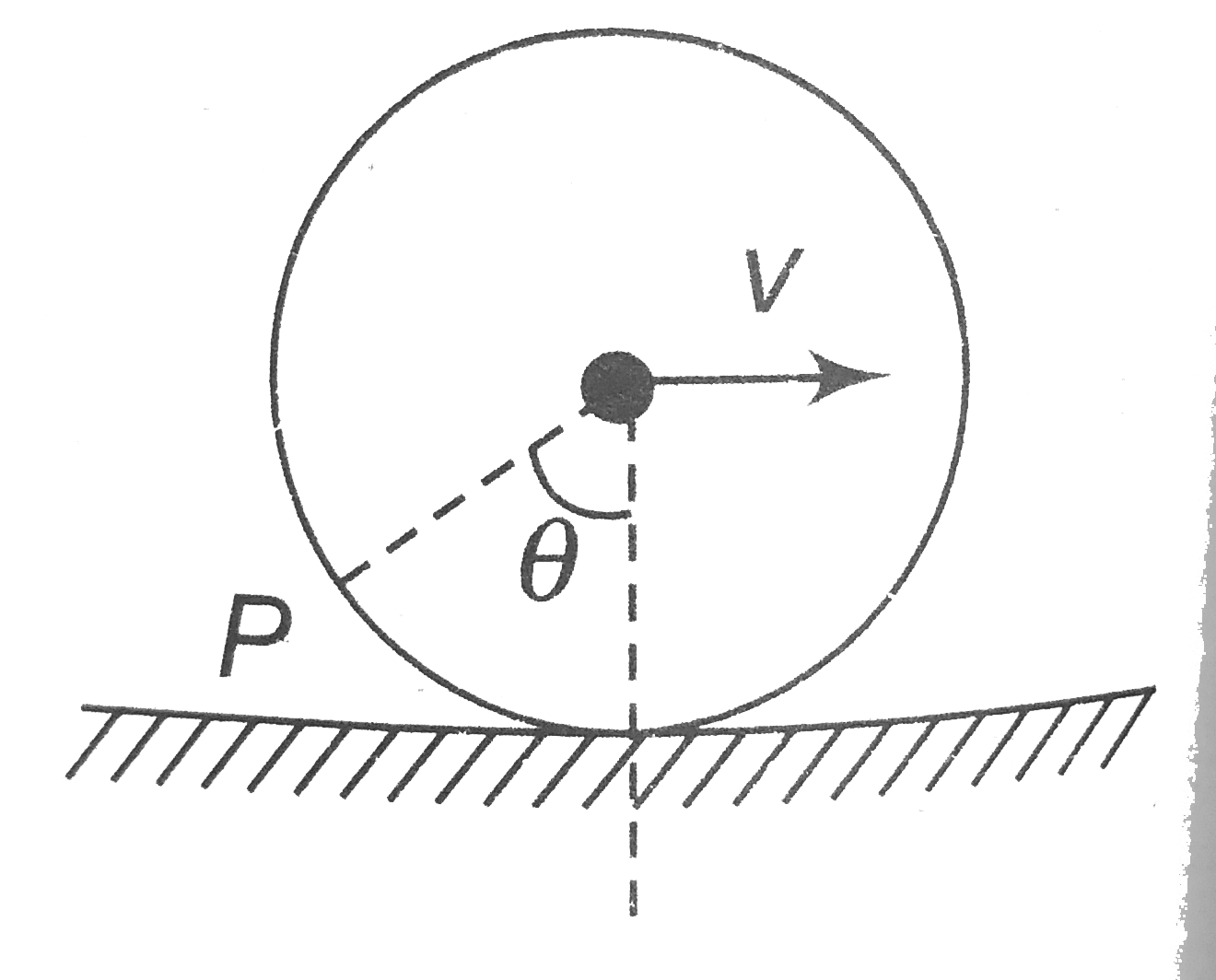
A hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View SolutionA disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
a. a point on the rim,
b. the middle point of the radius.
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View SolutionIf the speed of a particle moving at a relativistic speed is doubled, its linear momentum will
View SolutionA mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
View SolutionA hollow sphere rolls without slipping down a plane inclined at an angle of 30° to the horizontal. Its linear acceleration will be
View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View SolutionA small sphere of mass 1 kg is rolling without slipping with linear speed
v=√2007m/s

It leaves the inclined plane at point C.
Find the linear speed at point C.
View Solution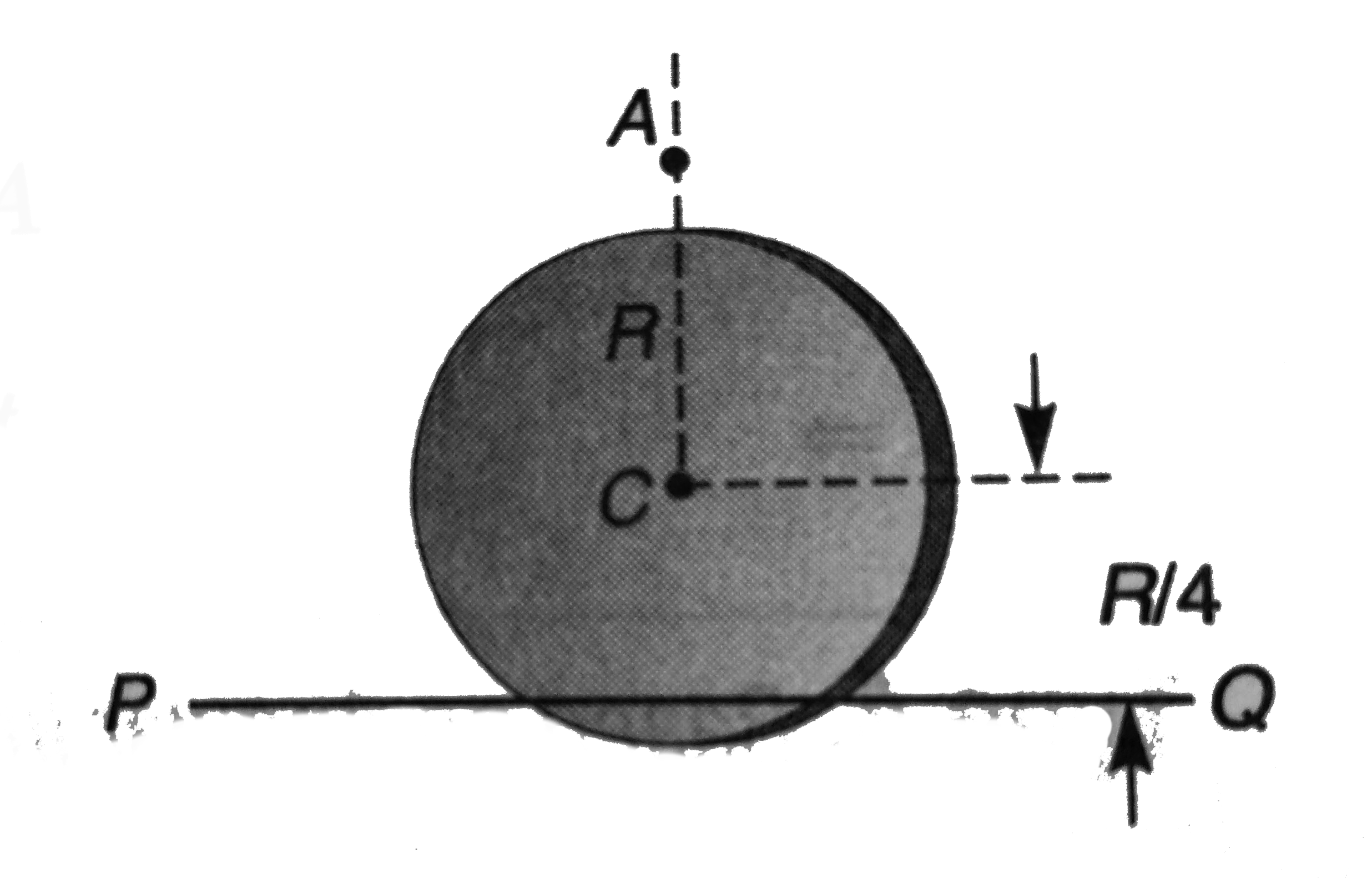
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View Solution
