Two men support a uniform horizontal beam at its two ends, if one of them suddenly lets go, the force exerted by the beam on the other man will
remain unaffected
increase
decrease
become unequal to the force exerted by him on the beam
The correct Answer is:3
To solve the problem, we need to analyze the situation step by step. Here’s how we can approach it:
Step 1: Understand the Initial Setup
We have a uniform horizontal beam supported at both ends by two men. The weight of the beam (mg) acts at its center. Initially, both men exert equal forces (normal reactions) on the beam to keep it in equilibrium.
Step 2: Calculate the Initial Forces
In equilibrium, the sum of the upward forces (normal reactions from both men) must equal the downward force (weight of the beam):
N+N=mg
Since both men exert equal forces, we can write:
2N=mg
Thus, the force exerted by each man is:
N=mg2
Step 3: Analyze the Situation When One Man Lets Go
When one man suddenly lets go, the beam will start to rotate about the point where the other man is still holding it. The weight of the beam still acts at the center.
Step 4: Set Up the Equation for Forces After One Man Lets Go
Let’s denote the normal reaction force exerted by the beam on the remaining man as N′. The net force acting on the beam in the downward direction is still mg, and the upward force is now just N′:
mg−N′=ma
Where a is the downward acceleration of the center of mass of the beam.
Step 5: Calculate the Torque and Angular Acceleration
To find the relationship between the linear acceleration a and the angular acceleration α, we can use the torque about the point where the remaining man is holding the beam:
- The torque due to the weight of the beam is:
τ=mg⋅L2
- The moment of inertia I of the beam about the pivot point is:
I=13mL2
Using Newton's second law for rotation:
τ=Iα
Thus:
mg⋅L2=13mL2α
From this, we can solve for α:
α=3g2L
Step 6: Relate Linear Acceleration to Angular Acceleration
The linear acceleration a of the center of mass is related to the angular acceleration by:
a=Rα
Where R=L2 (the distance from the pivot to the center of mass). Thus:
a=L2⋅3g2L=3g4
Step 7: Substitute Back to Find N′
Now we can substitute a back into the force equation:
mg−N′=m⋅3g4
Rearranging gives:
N′=mg−3mg4=mg(1−34)=mg4
Step 8: Compare the Forces
Initially, the force exerted by each man was mg2. After one man lets go, the force exerted by the remaining man is mg4.
Conclusion
Thus, the force exerted by the beam on the other man decreases from mg2 to mg4.
Final Answer
The force exerted by the beam on the other man will decrease.
---
We have a uniform horizontal beam supported at both ends by two men. The weight of the beam (mg) acts at its center. Initially, both men exert equal forces (normal reactions) on the beam to keep it in equilibrium.
In equilibrium, the sum of the upward forces (normal reactions from both men) must equal the downward force (weight of the beam):
N+N=mg
Since both men exert equal forces, we can write:
2N=mg
Thus, the force exerted by each man is:
N=mg2
When one man suddenly lets go, the beam will start to rotate about the point where the other man is still holding it. The weight of the beam still acts at the center.
Let’s denote the normal reaction force exerted by the beam on the remaining man as N′. The net force acting on the beam in the downward direction is still mg, and the upward force is now just N′:
mg−N′=ma
Where a is the downward acceleration of the center of mass of the beam.
To find the relationship between the linear acceleration a and the angular acceleration α, we can use the torque about the point where the remaining man is holding the beam:
- The torque due to the weight of the beam is:
τ=mg⋅L2
- The moment of inertia I of the beam about the pivot point is:
I=13mL2
Using Newton's second law for rotation:
τ=Iα
Thus:
mg⋅L2=13mL2α
From this, we can solve for α:
α=3g2L
The linear acceleration a of the center of mass is related to the angular acceleration by:
a=Rα
Where R=L2 (the distance from the pivot to the center of mass). Thus:
a=L2⋅3g2L=3g4
Now we can substitute a back into the force equation:
mg−N′=m⋅3g4
Rearranging gives:
N′=mg−3mg4=mg(1−34)=mg4
Initially, the force exerted by each man was mg2. After one man lets go, the force exerted by the remaining man is mg4.
Thus, the force exerted by the beam on the other man decreases from mg2 to mg4.
The force exerted by the beam on the other man will decrease.
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-1
4 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-2
5 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
Similar Questions
Two men support a uniform rod of mass M and length L at its two ends. If one of them suddenly withdraws, find the force excerted by the rod on the other man
(a) immediately after withdrawl and
(b) when the rod makes angle θ with vertical.
View SolutionThree identical particles force exerted on one body due to the other two.
View Solution
Knowledge Check
A tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. Determine the force exerted by the liquid at the other end.
AMω2L2BMω2LCMω2L4DMω2L22
A tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. The force exerted by the liquid at the other end is
View SolutionA uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end produces a ninety degree bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (a) If the coefficient of static friction between beam and floor is μs determine an expression for the maximum mass M that can be suspended from the top before the beam slips. (b) Determine the magnitude of the reaction force at the floor and the magnitude of the force exerted by the beam on the rope at P in terms of m,M and μs
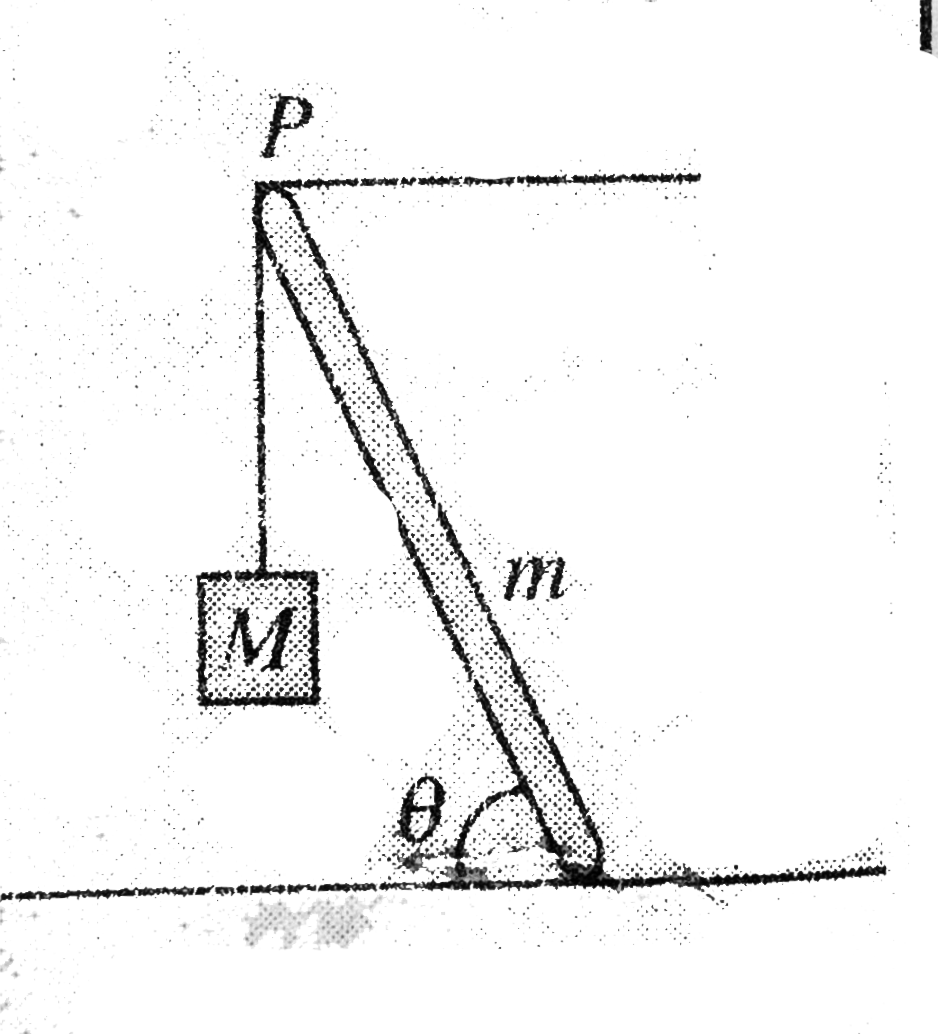 .
.
View SolutionA uniform chain of mass m and length l hangs on a thread and touches the surface of a table by its lower end. Thread breaks suddenly. Find the force exerted by the table on the chain when half of its length has fallen on the table. The fallen part does not form heap

View SolutionThe horizontal beam in figure weighs 150N, and its centre of gravity is at its centre. Find
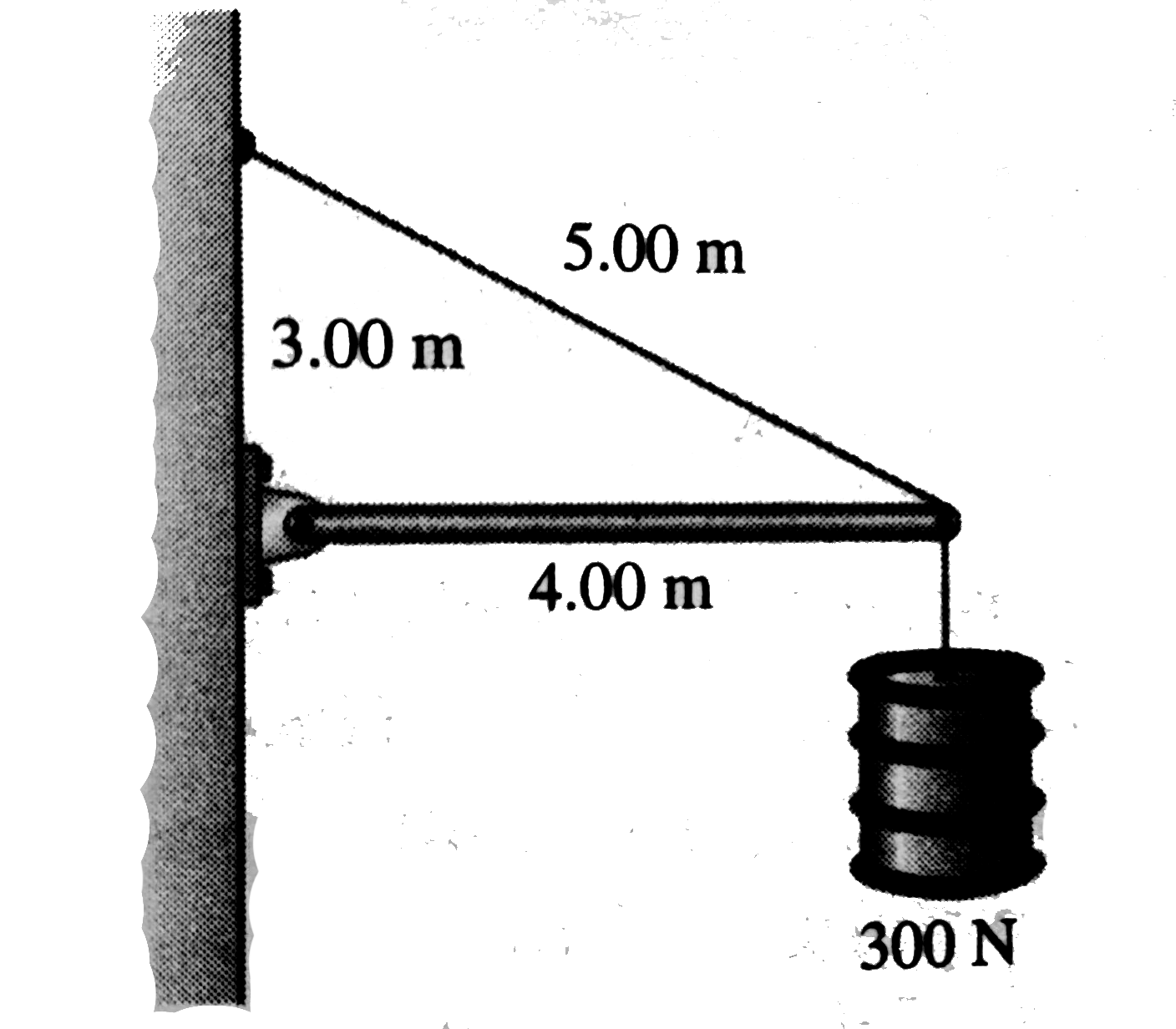
The horizontal and vertical components of the force exerted on the beam at the wall,
View SolutionTwo boys are holding a horizontal rod of length L and weight W through its two ends. If now one of the boys suddenly leaves the rod, what is the instantaneous reaction force experienced by the other boy ?
View SolutionOne end of a uniform rod of mas m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component
View SolutionThe sum of two integers is −14. If one of them is 11, then find the other.
View Solution
