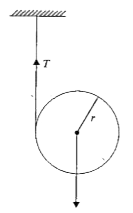
One end of a massless string is wound around a cylinder of mass 5 kg and radius 16' cm. The cylinder' is mounted symmetrically on a horizontal axle so 5 that It can freely rotate about its axis, to the other end of the string a mass of 500 gm is attached. Calculate the acceleration of the mass when it is released from rest.
To solve the problem step by step, we will analyze the forces acting on the mass and the torque acting on the cylinder.
Step 1: Identify the given values
- Mass of the cylinder (M) = 5 kg
- Radius of the cylinder (R) = 16 cm = 0.16 m
- Mass attached to the string (m) = 500 g = 0.5 kg
- Acceleration due to gravity (g) = 9.81 m/s² (approximately)
Step 2: Draw the free body diagram
For the mass (m):
- The gravitational force acting downward: Fg=mg=0.5×9.81=4.905N
- The tension (T) acting upward.
For the cylinder:
- The torque (τ) caused by the tension in the string: τ=T⋅R
Step 3: Write the equations of motion
For the mass (m):
- The net force acting on the mass is given by:
mg−T=ma
where a is the linear acceleration of the mass.
For the cylinder:
- The torque is related to the angular acceleration (α) by:
τ=Iα
where I is the moment of inertia of the cylinder. For a solid cylinder, I=12MR2.
- The relationship between linear acceleration (a) and angular acceleration (α) is:
a=Rα⇒α=aR
Step 4: Substitute the expressions
Substituting α in the torque equation:
T⋅R=I⋅aR
Substituting I:
T⋅R=(12MR2)⋅aR
This simplifies to:
T=12M⋅aR
Step 5: Substitute T in the mass equation
Now substitute T back into the equation for the mass:
mg−12M⋅aR=ma
Rearranging gives:
mg=ma+12M⋅aR
Factoring out a:
mg=a(m+12MR)
Thus,
a=mgm+12M
Step 6: Substitute the values
Now substituting the values:
a=0.5⋅9.810.5+12⋅5
Calculating the denominator:
=0.5+2.5=3
Thus,
a=4.9053≈1.635m/s2
Final Answer
The acceleration of the mass when it is released from rest is approximately 1.635m/s2.
---
- Mass of the cylinder (M) = 5 kg
- Radius of the cylinder (R) = 16 cm = 0.16 m
- Mass attached to the string (m) = 500 g = 0.5 kg
- Acceleration due to gravity (g) = 9.81 m/s² (approximately)
For the mass (m):
- The gravitational force acting downward: Fg=mg=0.5×9.81=4.905N
- The tension (T) acting upward.
- The torque (τ) caused by the tension in the string: τ=T⋅R
For the mass (m):
- The net force acting on the mass is given by:
mg−T=ma
where a is the linear acceleration of the mass.
- The torque is related to the angular acceleration (α) by:
τ=Iα
where I is the moment of inertia of the cylinder. For a solid cylinder, I=12MR2.
- The relationship between linear acceleration (a) and angular acceleration (α) is:
a=Rα⇒α=aR
Substituting α in the torque equation:
T⋅R=I⋅aR
Substituting I:
T⋅R=(12MR2)⋅aR
This simplifies to:
T=12M⋅aR
Now substitute T back into the equation for the mass:
mg−12M⋅aR=ma
Rearranging gives:
mg=ma+12M⋅aR
Factoring out a:
mg=a(m+12MR)
Thus,
a=mgm+12M
Now substituting the values:
a=0.5⋅9.810.5+12⋅5
Calculating the denominator:
=0.5+2.5=3
Thus,
a=4.9053≈1.635m/s2
The acceleration of the mass when it is released from rest is approximately 1.635m/s2.
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
Explore 11 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (LONG ANSWER QUESTIONS)
Explore 8 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
A mass M is supported by a massless string wound round a uniform cylinder ofmass M and radius R. On releasing the mass from rest, it will fall with acceleration?

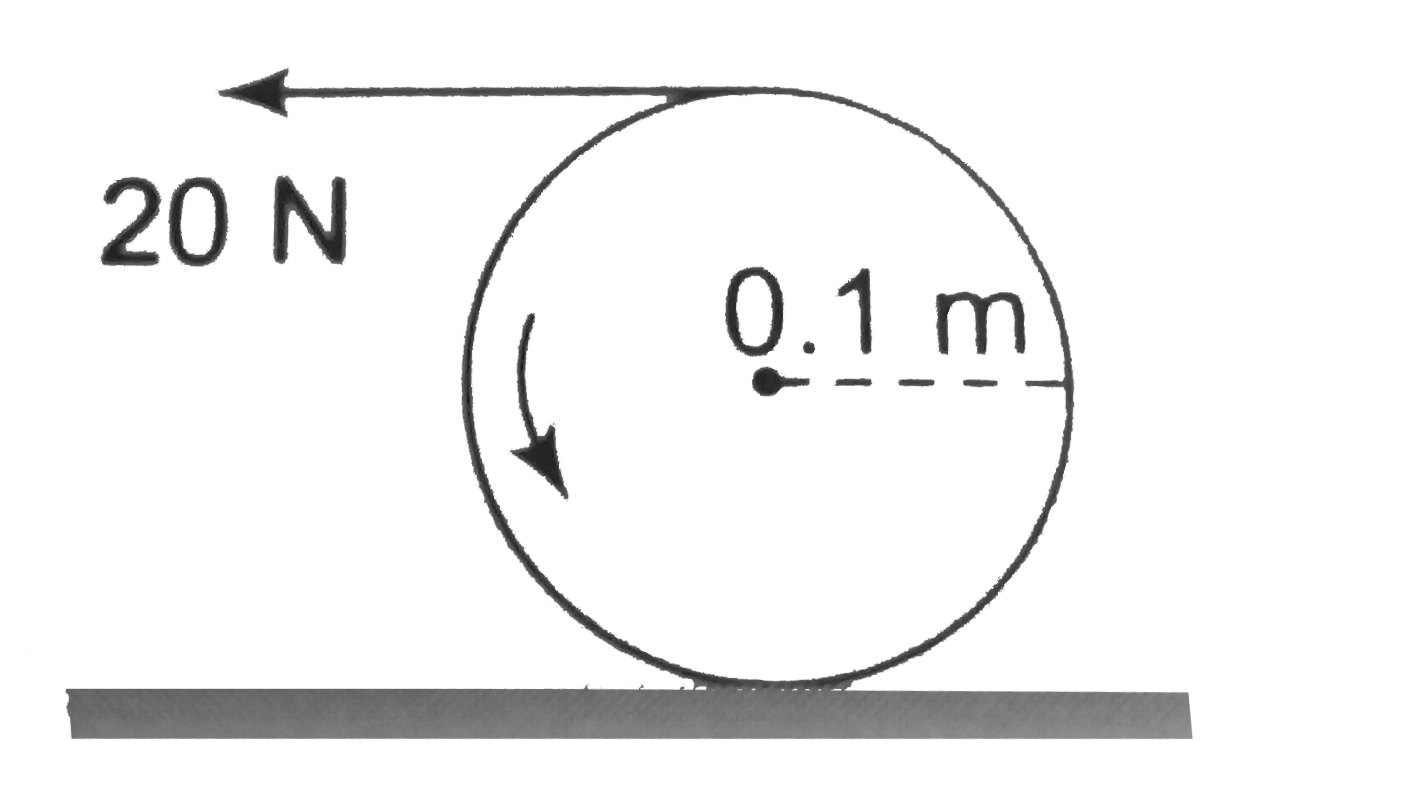
View SolutionA string is wound around a hollow cylinder of mass 5 Kg and radius 0.5 m. If the string is now pulled with a horizontal force of 40 N, the cylinder is rolling without slipping on a horizontal surface (see figure), then the angular acceleration of the cylinder will be (Neglect the mass and thickness of the string).

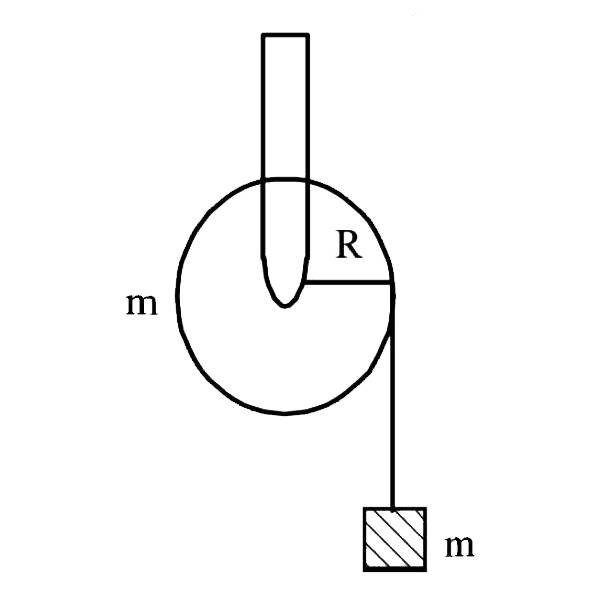
View SolutionA mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
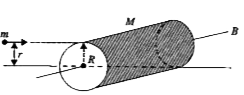
View SolutionA small body of mass 100 g moving with a velocity 2 m/s is strikes a solid cylinder of mass 2 kg and radius 20 cm. The cylinder is initially at rest and is mounted on a fixed horizontal axle that passes through the centre of mass. The line of motion of the small body is at a perpendicular lar distance of 15 cm from the centre of the cylinder. The small body strikes the cylinder and adheres to its surface. What is the angular speed of the system just after the collision ? Assume there is no friction.
View SolutionThe rope shown in figure is wound around a cylinder of mass 4kg and moment of inertia 0.02kgm2 about the cylinder axis. If the cylinder rolls without slipping, then the linear acceleration of its centre of mass is.
 .
.
View SolutionOn the surface of a solid cylinder of mass 2 kg and radius 25 cm a string is wound several times and the end of the string is held stationary while the cylinder is released from rest. What is the acceleration of the cylinder and the tension in the string ?
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View SolutionA load of mass m is attached to the end of a string wound on a cylinder of mass M and radius R. The string passes round a pulley.
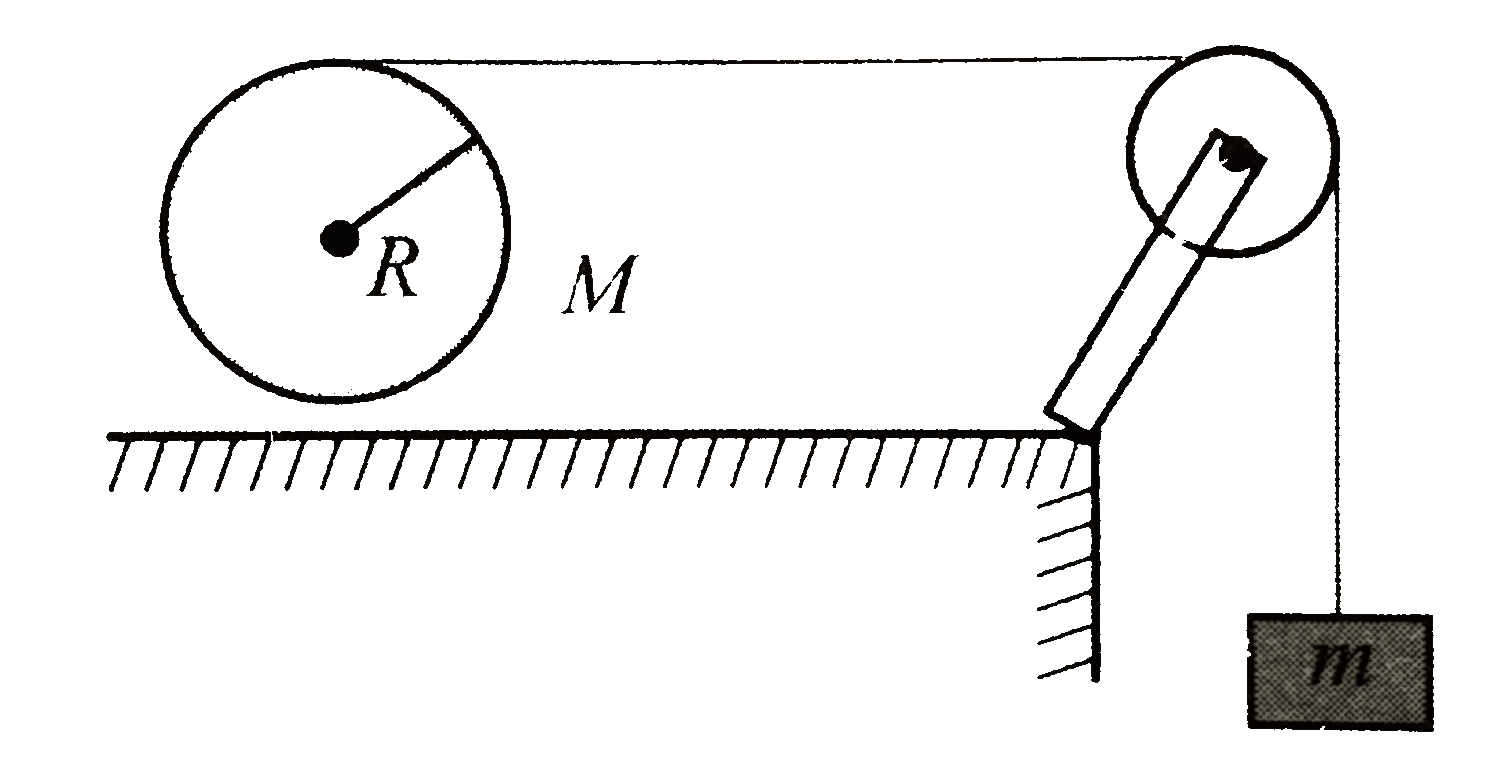
a. Find the acceleration of the cylinder M when it rolls.
b. If the coefficient of friction is μ. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls always
View SolutionA spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View Solution
in figure the cylinder of mass 10kg and radius 10 cm has a tape wrapped round it. The pully weighs 100 N and has a radius 5 cm. When the system is released the 5 kg mass comes down and the cylinder rolls without slipping. Calculate the acceleration and velocity of the mass as a function of time.
View Solution

