A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time πL/3v0 after the collision.
(i) 1/4, (ii) 2/3, (iii) v0/2√2
(i) If we take rod and particle as a system, the impulse between them will be internal. We can conserve the linear momentum of rod + particle’s system. Let VC and ω be the velocity and angular velocity of the CM just after collision.
Using conservation of linear momentum, we have
mv0=0+MvC..........(i)
Here in this case we can conserve angular momentum about any point on the rod.
And by conservation of angular momentum about the centre of mass of the rod, we get,
mv0L2=Iωor mv0L2=ML212ω..........(ii)
From Eqs.(i) and (ii), vC=mv0M and ω=6mv0ML
We can apply conservation of angular momentum about point of collision.
→Linitial=→Lfinal
0=I0ω(−ˆk)+MvCL2(ˆk)
ML212ω=MvcL2
which gives ωL=6vC........(iii)
Solving.(i) and (iii), we get the same results.
Since collision is completely elastic, therefore, KE before collision is equal to KE after collision.
12mv20=12M(Mv02)2+12ML212(6mv0ML)2
Which gives mM=14 and vC=V04.

Topper's Solved these Questions
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (True/False Type)
Explore 3 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (NUMERICAL VALUE TYPE)
Explore 15 Videos
- REVISION TEST-2 JEEBook:VMC MODULES ENGLISHChapter:REVISION TEST-2 JEEExercise:PHYSICS
Explore 25 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
Similar Questions
A rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
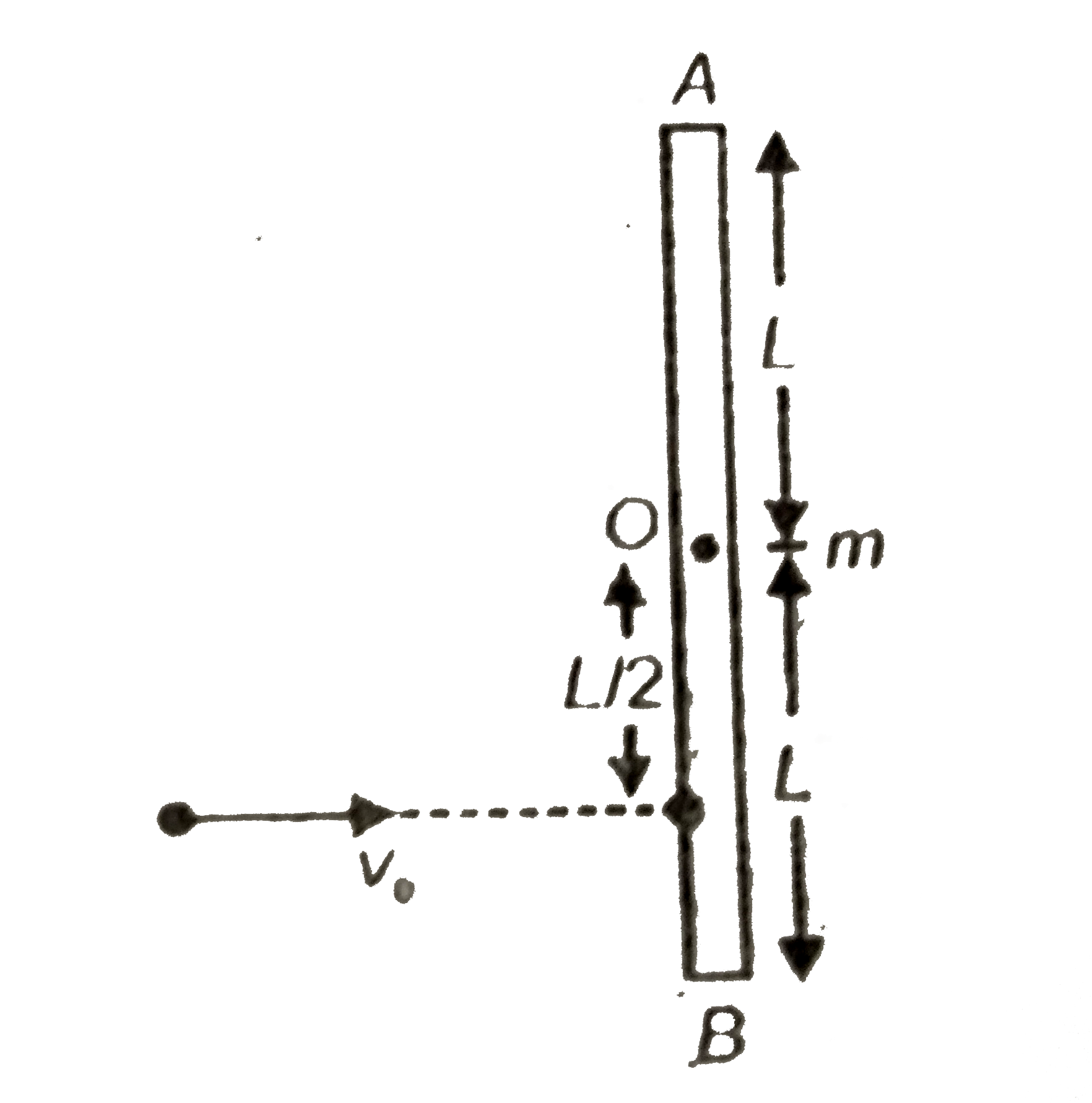
Angular velocity of rod just after collision is
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.

Angular velocity of rod just after collision is
View SolutionA rod AC of length l and mass m is kept on a horizontal smooth plane. It is free to rotate and move. A particle of same mass m moving on the plane with velocity v strikes the rod at point B making angle 37∘ with the rod. The collision is elastic. After collision,

View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View SolutionA slender rod of mass M and length L rests on a horizontal frictionless surface. The rod is pivoted about one of ends. The impulse of the force exerted on the rod by the pivot when the rod is struck by a blow of impulse J perpendicular to the rod at other end is
View SolutionA straight rod AB of mass M and length L is placed on a frictionless horizontal surface. A force having constant magnitude F and a fixed direction start acting at the end A. The rod is initially perpendicular to the force. The initial acceleration of end B is
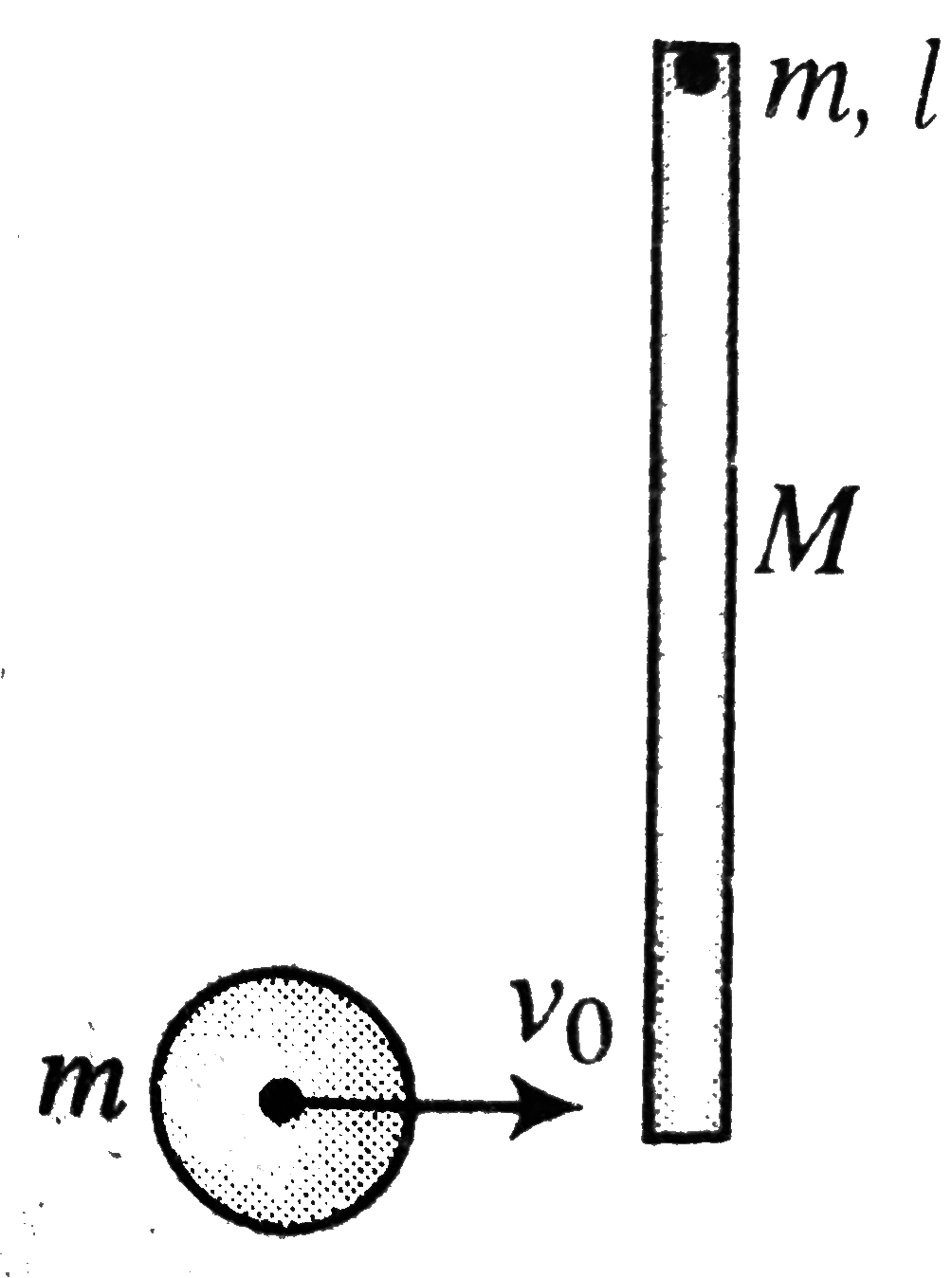
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA rod of mass m and length l in placed on a smooth table. An another particle of same mass m strikes the rod with velocity v0 in a direction perpendicular to the rod at distance x(<l/2) from its centre . Particle sticks to the end. Let ω be the angular speed of system after collision , then
As x is increased from 0 to l/2 , the angular speed ω.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View Solution