Question

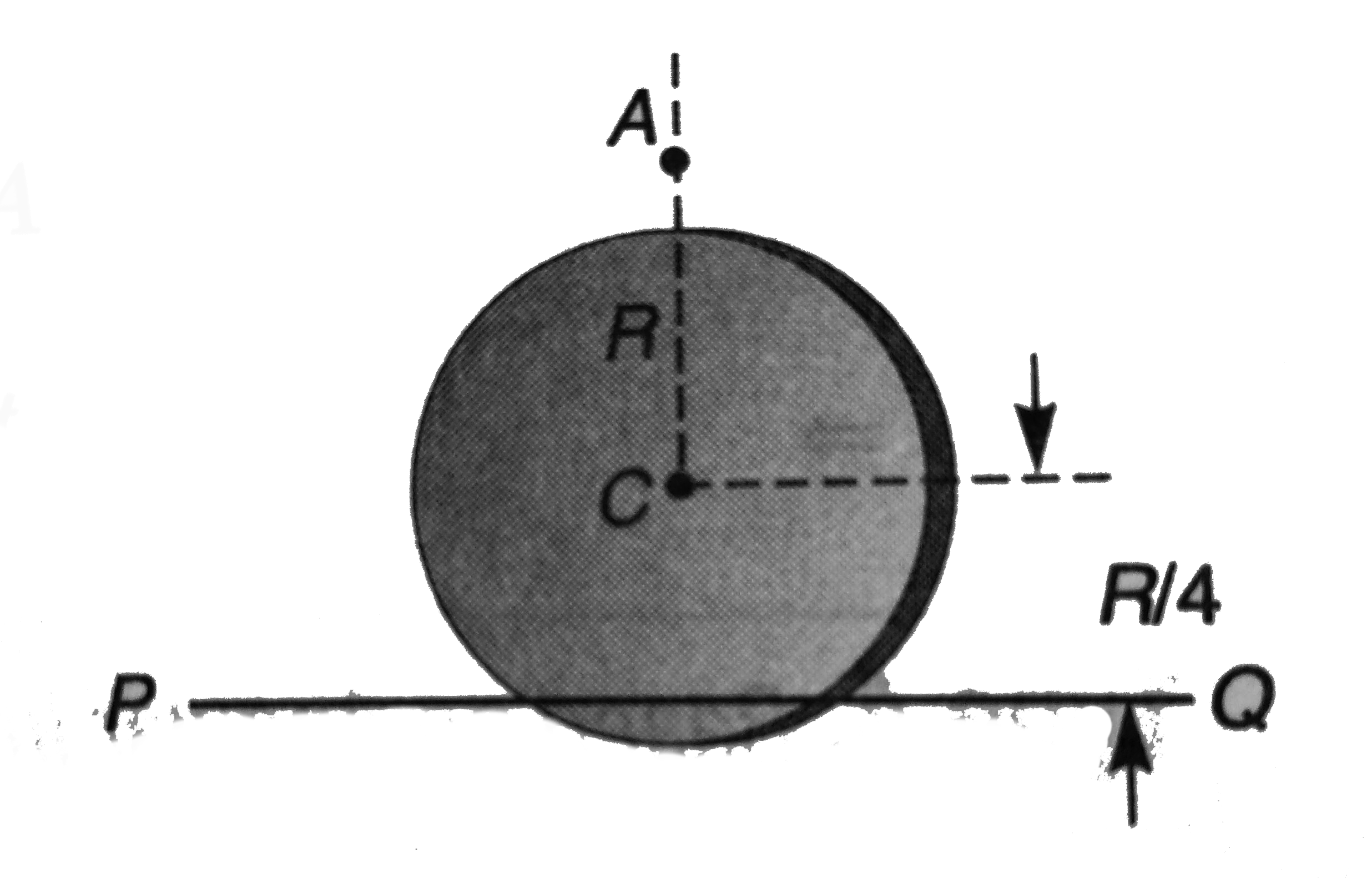
A uniform circular disc has radius $R$ and mass $m$. A particle, also of mass $m$, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance $R/4$ from the centre $C$ of the disc. The line AC is perpendicular to $PQ$. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.

Explanation

During the fal, the disc-mass system gains rotational kinetic energy. This is at the expenses of potential energy.
Applying conservation of mechanical energy, we get Initial total energy =Final total energy.

`mg(2R + (2R)/4) + mg(R + (2R)/4) =mgR + 1/2Iomega^(2)`
Where I = MI of the disc-mass system about PQ.
`=(mg)(10R)/4 + mg(6R)/4 = 4mR + 1/2Iomega^(2) rArr 3mgR = 1/2I omega^(2)`
`rArr omega =sqrt((6mgR)I)`.....(i)
`(I)_(PQ) =(I_("disc"))_(PQ) + (I_("mass"))PQ`
`=[(mR^(2))/4 + M(R/4)^(2)] + m((5R)/4)^(2)]`
[Therefore, MI of disc about the diameter `=(1//4)MR^(2)`]
`=(mR^(2) [4+1+25])/16 =(15 mr^(2))/8`.......(ii)
From Eqs. (i) and (ii), `omega = sqrt((6mg R xx 8)/(15mR^(2)))= sqrt((16g)/(5R))`
Let v be the velocity of mass m at the lowest point of rotation.
`v=omega(R + R/4), =sqrt((16g)/(5R)) xx (5R)/4 = sqrt(5gR)`.