A wedge of mass m and triangular cross- section (AB = BC = CA = 2R) is moving with a constant velocity −vˆI towards a sphere of radius R fixed on a smooth horizontal table as shown in figure. The wadge makes an elastic collision with the fixed sphere and returns along the same path without any rotaion. Neglect all friction and suppose that the wedge remains in contact with the sphere for a very shot time. Δt, during which the sphere exerts a constant force F on the wedge.
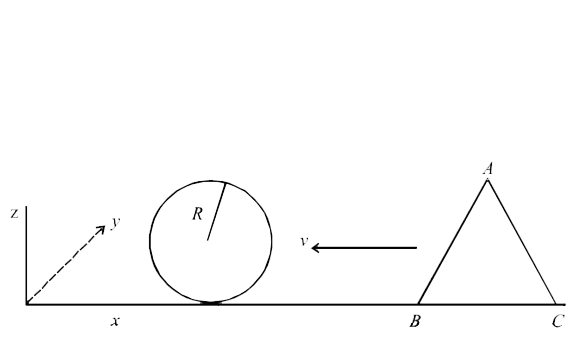
(a) Find the force F and also the normal force N exerted by the table on the wedge during the time Δt.
(b) Ler h denote the perpendicular distance between the centre of mass of the wedge and the line of action of F. Find the magnitude of the torque due to the normal force N about the centre of the wedge, during the interval Δt.
(i) →F=2mvΔtˆi−2mv√3Δtˆk,→N=(mg+2mv√3Δt)ˆk, (ii) 4mv√3Δth.
(i) The collision between sphere and wedge is elastic. As the sphere is fixed, hence the wedge will return with velocity vˆi.
Now, linear impulse in x-direction = change in momentum in x-direction.
∴(Fcos30∘)Δt=mv−(−mv)=2mv
∴F=2mvΔtcos30∘=4mv√Δt

→F=(2mvΔt)ˆi−2mv√3Δtˆk
Now consider the equilibrium of wedge in vertical direction. During collision.
N=mg+2mv√3Δt

or in vector form →N=mg+2mv√3Δtˆk
(ii) For rotational equilibrium of wedge about
its (CM), anticlockwise torque of F= Clockwise torque due to N
∴ Magnitude of torque of N about centre of mass = magnitude of torque of F about centre of mass =F.h.
|→τN|=(4mv√3Δt)h

Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)
3 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (NUMERICAL VALUE TYPE)
15 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
A solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
View SolutionAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :

View SolutionAll surfaces are smooth in following figure. Find F, such that block remain stationary with respect to wedge.

View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

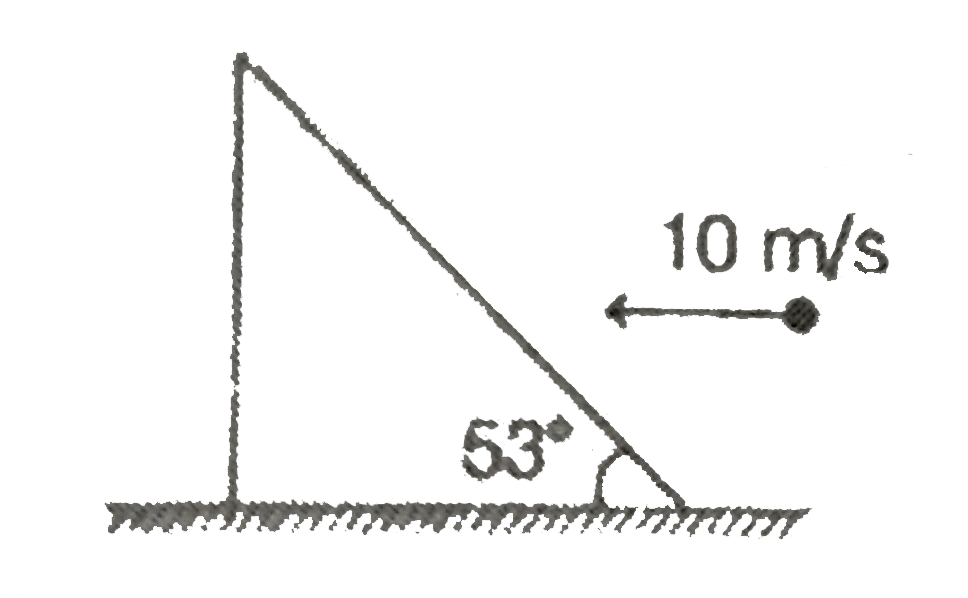
View SolutionA ball mass 2 kg moving horizontally with velocity 10 m/s hits a wedge of mass 5 kg placed on a horizontal surface as shown in the figure. Just after collision klvelocity of wedge is 3.2 m/s. There is no friction at any contact surface. Then (take sin 30∘=3/5)
View SolutionA sphere of mass m slides with velocity v on as frictionless surface towards a smooth inclined wall as shown in figure. If the collision with the wall is perfectly elastic find a. the impulse imparted by the wall on the sphere b the impulse imparted by the floor on the sphere.

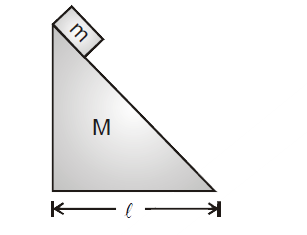
View SolutionA particle of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. Then the distance moved by the wedge as the particle reaches the foot of the wedge is :
View SolutionA solid sphere of radius 2.45m is rotating with an angular speed of 10rad/s. When this rotating sphere is placed on a rough horizontal surface then after sometime it starts pure rolling. Find the linear speed of the sphere after it starts pure rolling.
View SolutionA small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration a0=g. The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is

View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

View Solution
