A large open top container of negligible mass and uniform cross sectional area A has a small uniform cross sectional area a in its side wall near the bottom. The container is kept over a smooth horizontal floor and contains a liquid of density ρ and mass m0. Assuming that the liqud starts flowing through the hole A the acceleration of the container will be
g
g/50
g/100
g/10
The correct Answer is:B
To find the acceleration of the container when the liquid starts flowing through the hole, we can follow these steps:
1. Identify the velocity of efflux:
The velocity of the liquid flowing out through the hole at the bottom of the container can be determined using Torricelli's theorem. The velocity v of efflux is given by:
v=√2gh
where h is the height of the liquid column above the hole.
2. Calculate the mass flow rate:
The mass flow rate dmdt can be expressed in terms of the density ρ and the volume flow rate. The volume flow rate Q through the hole is given by:
Q=a⋅v=a⋅√2gh
where a is the cross-sectional area of the hole. Thus, the mass flow rate becomes:
dmdt=ρQ=ρa√2gh
3. Determine the force due to the efflux:
The force F exerted on the container due to the liquid flowing out can be calculated using the rate of change of momentum. The force is given by:
F=dmdt⋅v=(ρa√2gh)⋅√2gh=ρa(2gh)
4. Calculate the mass of the liquid in the container:
The mass m of the liquid in the container at any instant can be expressed as:
m=ρV=ρAh
where A is the cross-sectional area of the container and h is the height of the liquid.
5. Find the acceleration of the container:
The acceleration a of the container can be found using Newton's second law, F=ma. Thus, the acceleration is:
a=Fm=ρa(2gh)ρAh
Simplifying this expression, we find:
a=2agA
Final Result:
The acceleration of the container is:
a=2agA
The velocity of the liquid flowing out through the hole at the bottom of the container can be determined using Torricelli's theorem. The velocity v of efflux is given by:
v=√2gh
where h is the height of the liquid column above the hole.
The mass flow rate dmdt can be expressed in terms of the density ρ and the volume flow rate. The volume flow rate Q through the hole is given by:
Q=a⋅v=a⋅√2gh
where a is the cross-sectional area of the hole. Thus, the mass flow rate becomes:
dmdt=ρQ=ρa√2gh
The force F exerted on the container due to the liquid flowing out can be calculated using the rate of change of momentum. The force is given by:
F=dmdt⋅v=(ρa√2gh)⋅√2gh=ρa(2gh)
The mass m of the liquid in the container at any instant can be expressed as:
m=ρV=ρAh
where A is the cross-sectional area of the container and h is the height of the liquid.
The acceleration a of the container can be found using Newton's second law, F=ma. Thus, the acceleration is:
a=Fm=ρa(2gh)ρAh
Simplifying this expression, we find:
a=2agA
The acceleration of the container is:
a=2agA
Topper's Solved these Questions
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE MAIN (LEVEL - 1 )
Explore 31 Videos
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:IMPECCABLE
Explore 53 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Advanced (Archive)
Explore 78 Videos
Similar Questions
A large open top container of negligible mass and uniform cross sectional area A a has a small hole of cross sectional area A/100 in its side wall near the bottom. The container is kept on a smooth horizontal floor and contains a liquid of density ρ and mass M0. Assuming that the liquid starts flowing out horizontally through the hole at t=0, calculate a the acceleration of the container and its velocity when 75% of the liquid has drained out.
View SolutionA fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
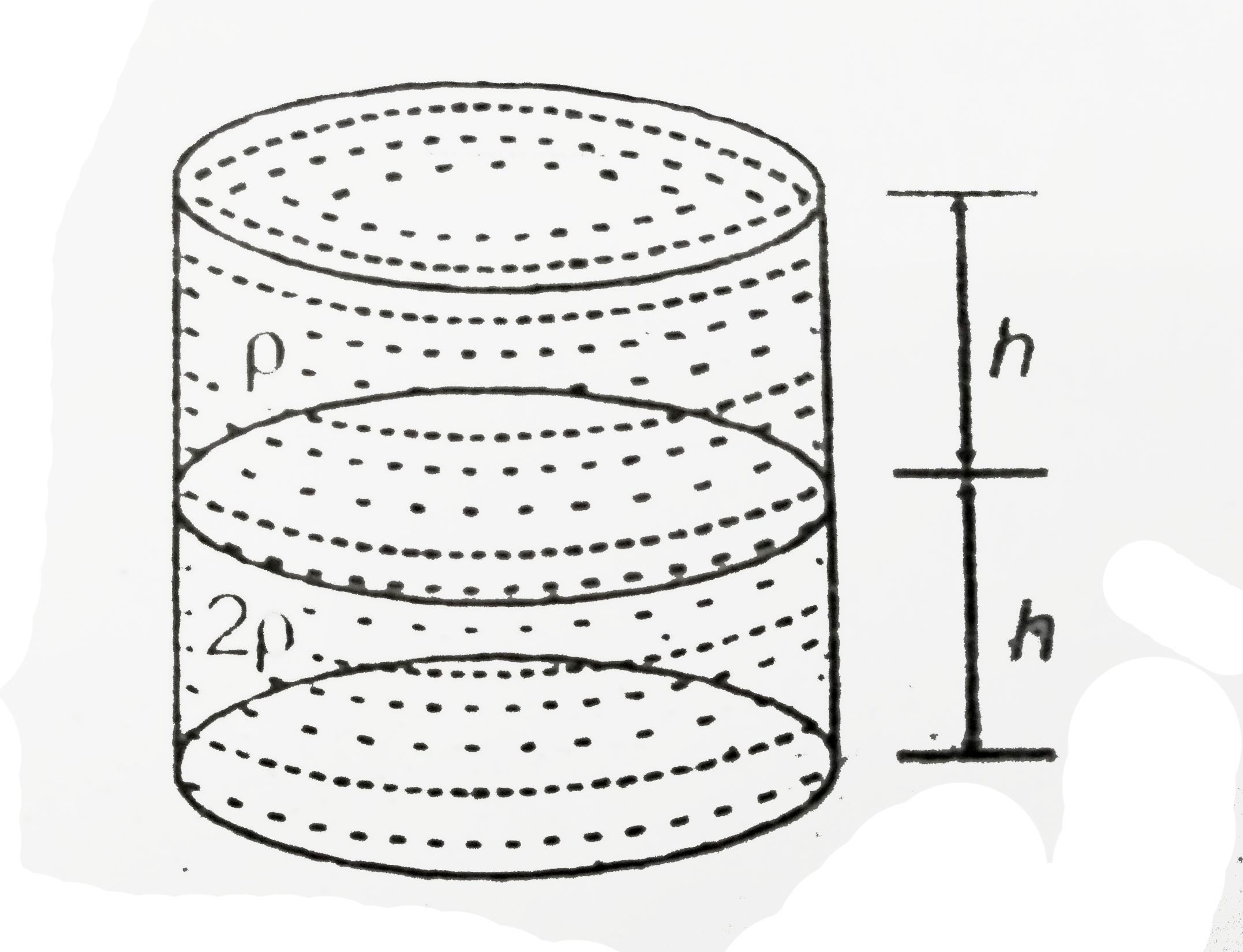
View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
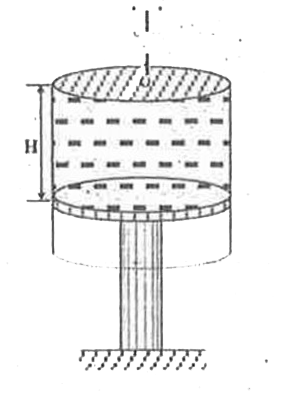
View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H )
Speed of the liquid with which it comes out of the vessel is

View SolutionIn the adjacent figure a cylindrical vessel of mass M and cross - sectional area A is placed inverted on a fixed smooth piston of same cross - sectional area fixed to the ground . The space between the cylinder and priston is completely filled with liquid of density ρ . There is a small office of cross - sectional area a (a<<A) at the top top portion of this vessel . ( intially length of the liquid column in the vessel is H ).Find the speed of the vessel with which it move
View SolutionA uniform ring having mass m, radius R, cross section area of the wire A and young’s modulus Y is rotating with an angular speed ω(ω is small) on a smooth horizontal surface. Which of the following options is correct :
View SolutionA rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
View SolutionA horizontal tube of uniform cross-sectional area A is bent in the form of U as shown in figure. If the liquid of density ρ enters and leaves the tube with velcity v, then the extermal force F requried to hold the bend stationary is

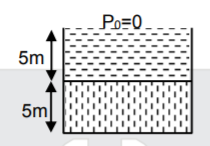
View SolutionTwo liquid columns of same height 5m and densities ρ and 2ρ are filled in a container of uniform cross sectional area. Then ratio of force exerted by the liquid on upper half of the wall to lower half of the wall is.
View SolutionA container of large uniform cross sectional area A, resting on horizontal surface, holds two immiscible non viscous and incompressible liquids of density d and 2d, each of height H2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A tiny hole of area (s(s<<A) is punched on the vertical side of the container at a height h(h<H2). Determine

the initial speed of efflux of the liquid at the hole
View Solution
