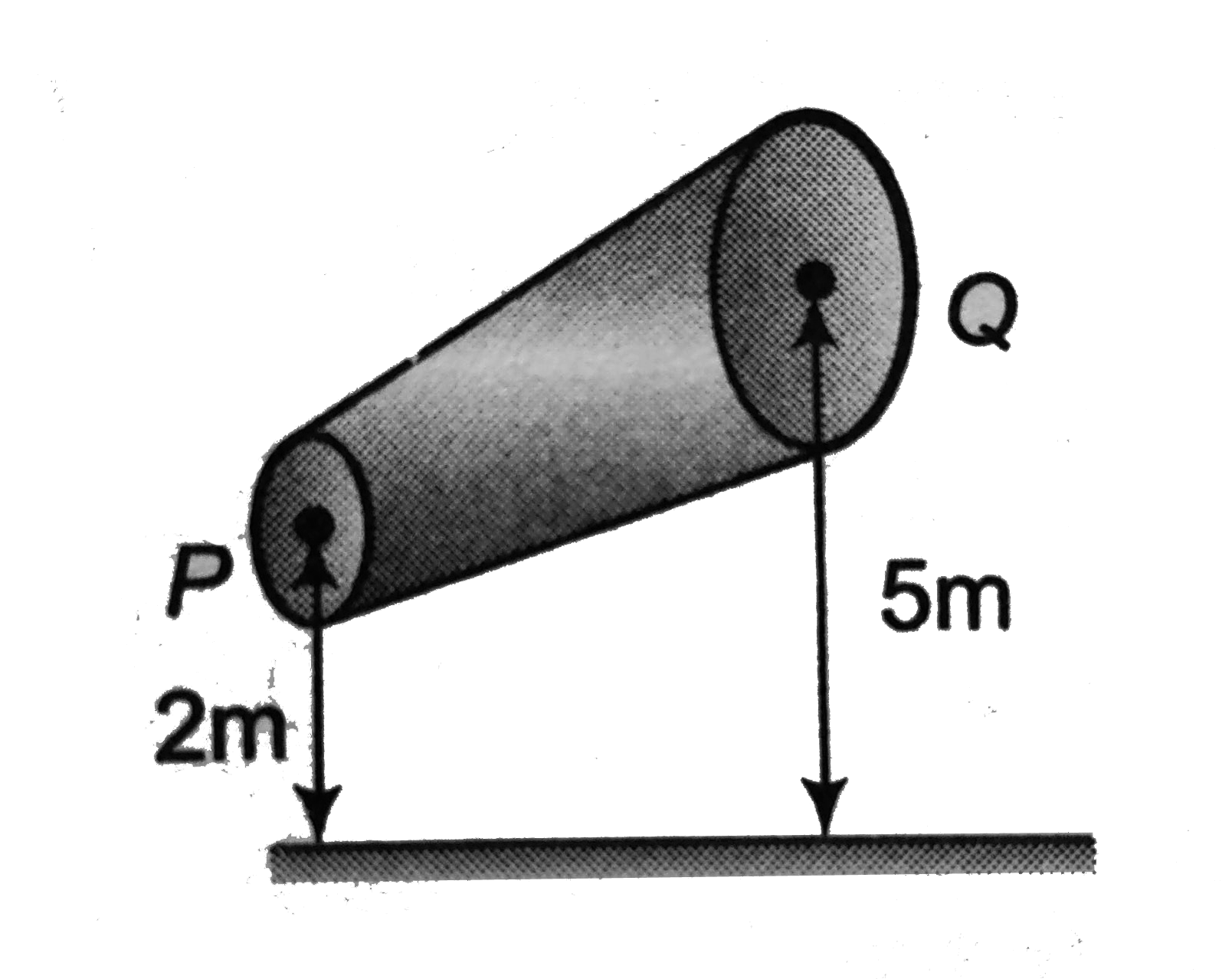
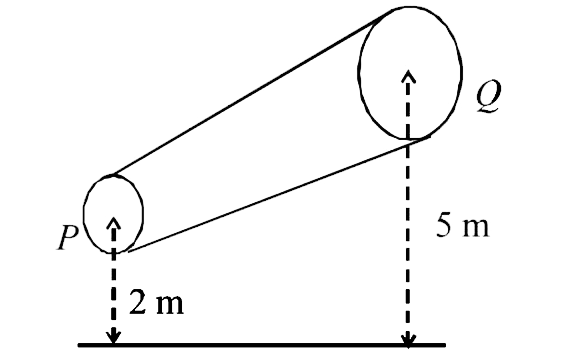
A non-viscous liquid of constant density 1000kg/m3 flows in a streamline notion along a tube of variable cross-section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross-section of the tube at two points P and Q at heights of 2m and 5m are respectively 4×103m2 and 8×10−3m2. The velocity of the liquid at point P is 1m/s. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q. Take g=9.8m/s2.
zero
29400J/m3
−29400J/m3
29025J/m3
The correct Answer is:D
Given A1=4×10−3m2,A2=8×10−3m2,h1=2m,h2=5m,v1=1m/sandρ=103kg/m3
From continuity equation, we have A1v1=A2v2orv2=(A1A2)v1
or v2=(4×10−38×10−3)(1m/s)⇒v2=12m/s
Applying Bernoulli's equation at sections 1 and 2
p1+12ρv21+ρgh1=p2+12ρv22+ρgh2
or p1−p2=ρg(h2−h1)+12ρ(v22−v21) ...(i)
(a) Work done per unit volume by the pressure as the fluid flows from P to Q.
W1=p1−p2=ρh(h2−h1)+12ρ(v22−v21) [From equation (i) ]
={(10)3(9.8)(5−2)+12(10)3(14−1))}=[24900−375]=29025J/m3
Topper's Solved these Questions
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )
31 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
Similar Questions
A non-viscous liquid of constant density 1000kg/m3 flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two point P and Q at heights of 2 metres and 5 metres are respectively 4×10−3m2 and 8×10−3m2. The velocity of the liquid at point P is 1m/s. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q.
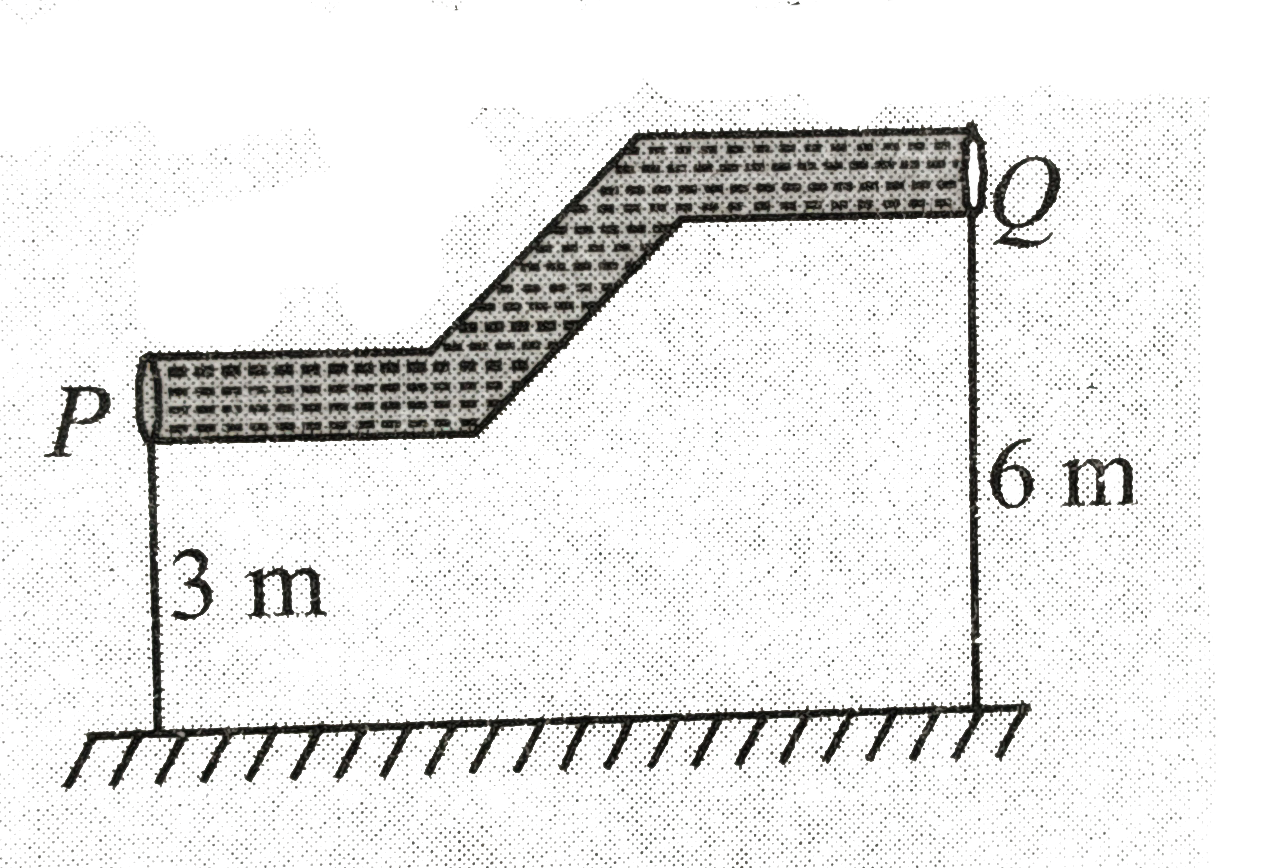
View SolutionA non-viscous liquid of constant density 500kg/m3 flows in a variable cross-sectional tube. The area of cross section of the tube at two points P and Q at heights of 3m and 6m are 2×10−3m3 and 4×10−3m3, respectively. Find the work done per unit volume by the forces of gravity as the fluid flows from point P to Q.
View SolutionA non viscous liquid of constant density 103kg/m3 flows in stream line motion along a vertical tube PQ of variable cross-section. Height of P and Q are 2m and 2.5m respectively. Area of tube at Q is equal to 3 times the area of tube at 'P'. Then work done per unit volume by pressure as liquid flows from P and Q. Speed of liquid at 'P' is 3m/s.
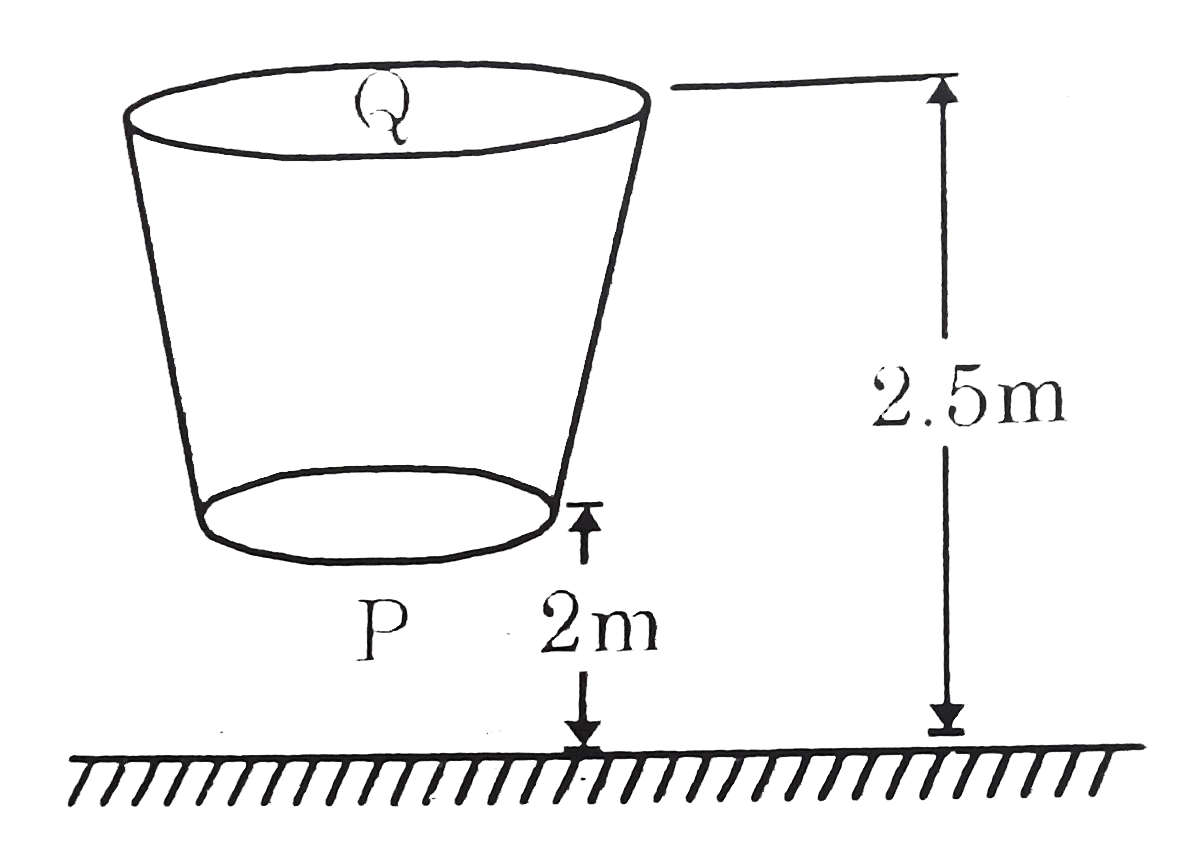
View SolutionA non viscous liquid of constant density 103kg/m3 flows in stream line motion along a vertical tube PQ of variable cross-section. Height of P and Q are 2m and 2.5m respectively. Area of tube at Q is equal to 3 times the area of tube at 'P'. Then work done per unit volume by pressure as liquid flows from P and Q. Speed of liquid at 'P' is 3m/s.
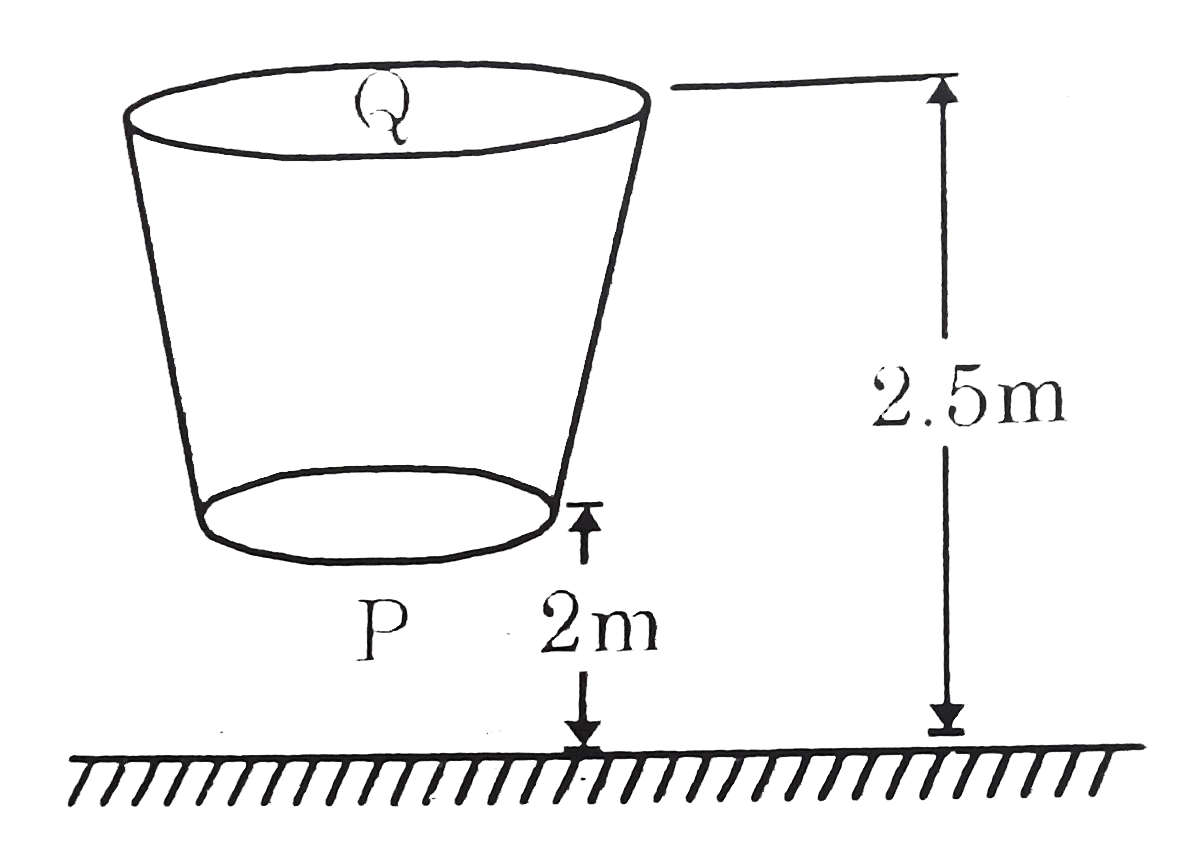
View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View SolutionWater flows through the tube shown in figure. The areas of cross section of the wide and the narrow portions of the tube are 5cm2and2cm2 respectively. The rate of flow of water through the tube is 500cm3s−1 . Find the difference of mercury levels in the U-tube.

View SolutionWater enters into a smooth horizontal tapering tube with a speed 2 m/sec and emerges out of the tube with a speed 8 m/sec . Find the ratio of the radii of cross sections of the tube at these two ends.
View SolutionA horizontal pipe of area of cross-section a and 3a respectively, then the ratio of velocity of flow at two different cross-section (If flow is streamline) is
View SolutionThe mass of the liquid flowing per second per unit area of cross-section of the tube is proportional to (pressure difference across the ends)^(n) and (average velocity of the liquid)^(m) . Which of the following relations between m and n is correct?
View Solution_S01_083_Q01.png)
Water (density ρ) is flowing through the uniform tube of cross-sectional area A with a constant speed v as shown in the figure. Find the magnitude of force exerted by the water on the curved corner of the tube is (neglect viscous forces)
View Solution
