The mass of the liquid flowing per second per unit area of cross-section of the tube is proportional to (pressure difference across the ends)^(n) and (average velocity of the liquid)^(m) . Which of the following relations between m and n is correct?
m=n
m=−n
m2=n
m=−n2
The correct Answer is:B
To solve the problem, we need to establish a relationship between the mass flow rate of a liquid (per second per unit area) and the pressure difference and average velocity of the liquid using dimensional analysis.
1. Understanding the Problem:
We are given that the mass flow rate ˙m (mass per unit time per unit area) is proportional to the pressure difference P raised to the power n and the average velocity v raised to the power m. This can be expressed as:
˙m∝Pnvm
2. Writing the Equation:
We can write the equation as:
˙m=kPnvm
where k is a proportionality constant.
3. Dimensional Analysis:
The dimensions of the quantities involved are:
- Mass flow rate ˙m: (M)(T−1)(L−2)
- Pressure P: (M)(L−1)(T−2)
- Velocity v: (L)(T−1)
4. Expressing Dimensions:
The dimensional formula for each term can be expressed as:
Dimensions of ˙m=(M)(T−1)(L−2)
Dimensions of Pn=(Mn)(L−n)(T−2n)
Dimensions of vm=(Lm)(T−m)
5. Combining Dimensions:
Now, we combine the dimensions of pressure and velocity:
Pnvm=(Mn)(L−n)(T−2n)⋅(Lm)(T−m)=(Mn)(Lm−n)(T−2n−m)
6. Setting Up the Equation:
Now, we equate the dimensions of both sides:
(M)(T−1)(L−2)=(Mn)(Lm−n)(T−2n−m)
7. Comparing Dimensions:
- For mass (M):
1=n(1)
- For length (L):
−2=m−n(2)
- For time (T):
−1=−2n−m(3)
8. Solving the Equations:
From equation (1), we have:
n=1
Substituting n=1 into equation (2):
−2=m−1⟹m=−1
9. Finding the Relationship:
Thus, we have:
m=−n
10. Conclusion:
The correct relationship between m and n is:
m=−n
Therefore, the answer is option 2.
We are given that the mass flow rate ˙m (mass per unit time per unit area) is proportional to the pressure difference P raised to the power n and the average velocity v raised to the power m. This can be expressed as:
˙m∝Pnvm
We can write the equation as:
˙m=kPnvm
where k is a proportionality constant.
The dimensions of the quantities involved are:
- Mass flow rate ˙m: (M)(T−1)(L−2)
- Pressure P: (M)(L−1)(T−2)
- Velocity v: (L)(T−1)
The dimensional formula for each term can be expressed as:
Dimensions of ˙m=(M)(T−1)(L−2)
Dimensions of Pn=(Mn)(L−n)(T−2n)
Dimensions of vm=(Lm)(T−m)
Now, we combine the dimensions of pressure and velocity:
Pnvm=(Mn)(L−n)(T−2n)⋅(Lm)(T−m)=(Mn)(Lm−n)(T−2n−m)
Now, we equate the dimensions of both sides:
(M)(T−1)(L−2)=(Mn)(Lm−n)(T−2n−m)
- For mass (M):
1=n(1)
- For length (L):
−2=m−n(2)
- For time (T):
−1=−2n−m(3)
From equation (1), we have:
n=1
Substituting n=1 into equation (2):
−2=m−1⟹m=−1
Thus, we have:
m=−n
The correct relationship between m and n is:
m=−n
Therefore, the answer is option 2.
Topper's Solved these Questions
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Match the column
6 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
Similar Questions
The volume of a liquid (V) flowing per second through a cylindrical tube depends upon the pressure gradient (p/l) radius of the tube (r) coefficient of viscosity (η) of the liquid by dimensional method the correct formula is
View SolutionThe volume V of a liquid crossing through a tube is related to the area of cross-section A, velocity v and time t as VαAavbtc which of the following is correct ( given a≠1 )
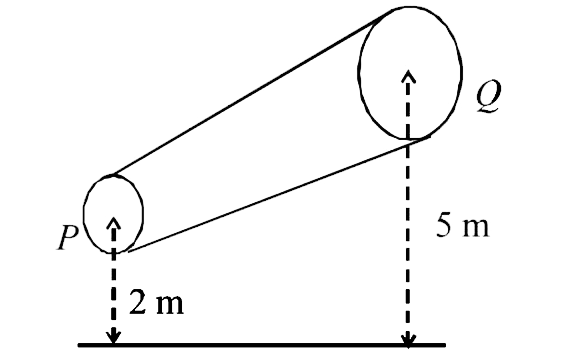
View SolutionA non-viscous liquid of constant density 1000kg/m3 flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two point P and Q at heights of 2 metres and 5 metres are respectively 4×10−3m2 and 8×10−3m2. The velocity of the liquid at point P is 1m/s. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q.
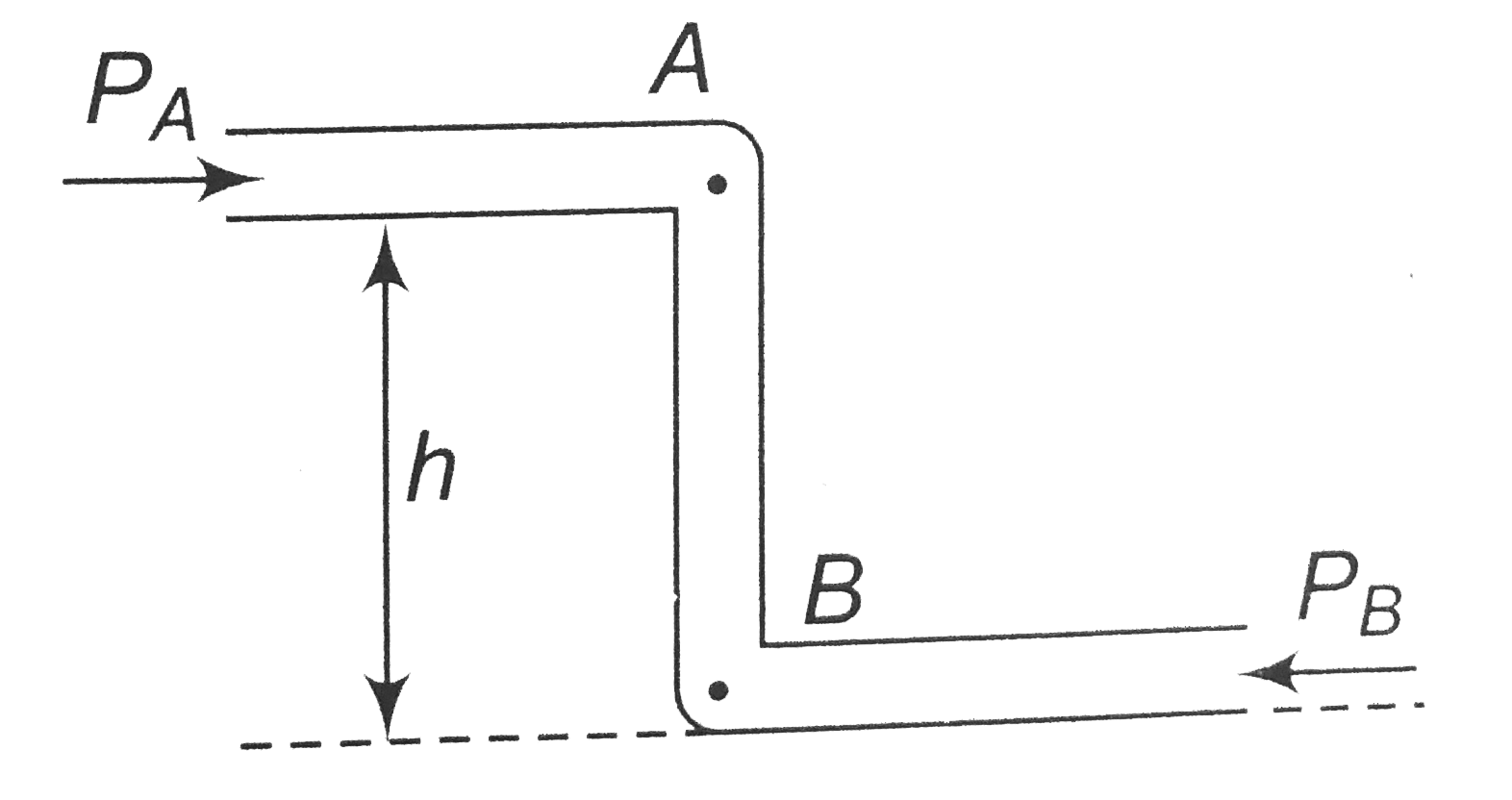
View SolutionFigure shows an ideal fluid flowing through a uniform cross-sectional tube in the vertical tube with liquid velocities vA and vB and pressure PA and PB. Knowing that offers no resistance to fluid flow then which of the following is true.
View SolutionThe length of a current-carrying cylindrical conductor is l, its area of cross-section is A, the number density of free electrons in it is n, and the drift velocity of electrons in it is vd . The number of electrons passing through a particular cross-section of the conductor per unit time is given by:
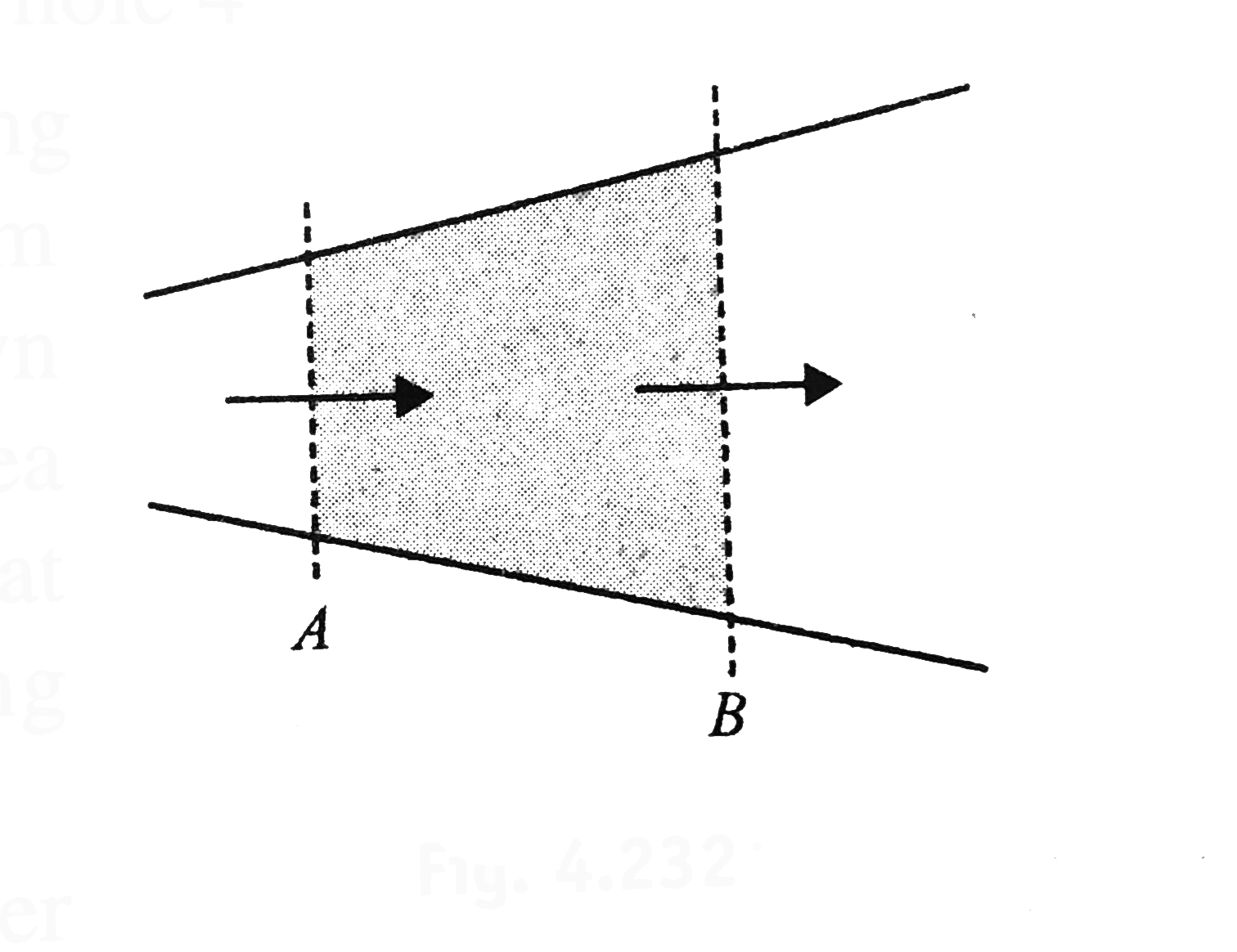
View SolutionA non-viscous liquid is flowing through a non-uniform pipe from section A to section B as shown in the figure. Cross sectional area of the pipe at A is less than that at B. Which of the following statements are correct?
View SolutionWhat is the area of cross-section of a body in m2, when it exerts a force of 50 N and produces a pressure of 2000 Pa?
View SolutionFigure shows a liquid flowing through a tube at the rate of 0.1m3/s. The tube is branched into two semicircular tubes of cross-sectional area A/3 and 2A/3. The velocity of liquid at Q is (the cross section of the main tube is A=10−2m2 and vp=20m/s)

View SolutionIn this figure, an ideal liquid flows through the tube having uniform area of cross-section and is held in vertical plane. Find the ratio of speed of liquid at A and B and also find the pressure difference between- these points.

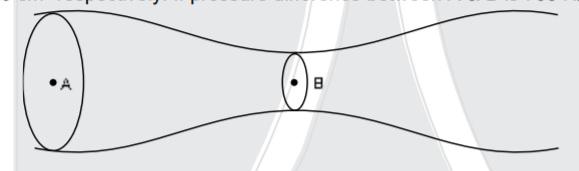
View SolutionAn ideal liquid (water) flowing through a tube of non-uniform cross section area at A and B are 40cm2 and 20cm2 respectively. If pressure difference between A & B is 700 Nm2 then volume flow rate is
View Solution
