In terms of basic units of mass (M), length (L), time (T), and charge (Q), the dimensions of magnetic permeability of vacuum (μ0) would be
[MLQ−2]
[LT−1Q−1]
[ML2T−1Q−2]
[LTQ−1]
The correct Answer is:A
To find the dimensions of the magnetic permeability of vacuum (µ₀) in terms of the basic units of mass (M), length (L), time (T), and charge (Q), we can use the relationship derived from the force between two parallel current-carrying wires.
1. Understand the Relationship:
The force per unit length (F/L) between two parallel wires carrying currents I₁ and I₂ separated by a distance r is given by the formula:
FL=μ0I1I22πr
Rearranging this gives:
μ0=F⋅2πrI1I2
2. Identify Dimensions:
We need to find the dimensions of each term in the equation:
- Force (F) has the dimensions of mass times acceleration:
(F)=MLT−2
- Distance (r) has the dimensions of length:
(r)=L
- Current (I) is defined as the rate of flow of charge, which gives it the dimensions:
(I)=QT−1
3. Substitute Dimensions into the Equation:
Now substituting the dimensions into the equation for µ₀:
μ0=(MLT−2)⋅(L)(QT−1)⋅(QT−1)
4. Simplify the Expression:
This simplifies to:
μ0=MLT−2⋅LQ2T−2=ML2T−2Q2
5. Final Dimensions:
Rearranging gives us:
μ0=ML2Q−2T−2
Thus, the dimensions of magnetic permeability of vacuum (µ₀) are:
(μ0)=MLQ−2
Final Answer:
The dimensions of magnetic permeability of vacuum (µ₀) are:
(μ0)=MLQ−2
The force per unit length (F/L) between two parallel wires carrying currents I₁ and I₂ separated by a distance r is given by the formula:
FL=μ0I1I22πr
Rearranging this gives:
μ0=F⋅2πrI1I2
We need to find the dimensions of each term in the equation:
- Force (F) has the dimensions of mass times acceleration:
(F)=MLT−2
- Distance (r) has the dimensions of length:
(r)=L
- Current (I) is defined as the rate of flow of charge, which gives it the dimensions:
(I)=QT−1
Now substituting the dimensions into the equation for µ₀:
μ0=(MLT−2)⋅(L)(QT−1)⋅(QT−1)
This simplifies to:
μ0=MLT−2⋅LQ2T−2=ML2T−2Q2
Rearranging gives us:
μ0=ML2Q−2T−2
Thus, the dimensions of magnetic permeability of vacuum (µ₀) are:
(μ0)=MLQ−2
The dimensions of magnetic permeability of vacuum (µ₀) are:
(μ0)=MLQ−2
Topper's Solved these Questions
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Match the column
6 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
Similar Questions
Using mass (M), length (L), time (T) and current (A) as fundamental quantities, the dimensions of permeability are :
View SolutionUsing mass(M),length(L),time(T) and current(A)as fundamental quantites the demension of permeability is
View SolutionUsing mass (M), length (L), time (T) and current (A) as fundamental quantities, the dimension of permittivity is:
View SolutionUsing mass (M), length (L), time (T) and current (A) as fundamental quantities, the dimension of permittivity is:
View SolutionIf the velocity (V) , acceleration (A) , and force (F) are taken as fundamental quantities instead of mass (M) , length (L),andtime(T) , the dimensions of young's modulus (Y) would be
View SolutionUsing mass (M) , length (L) , time (T) , and electric current (A) as fundamental quantities , the dimensions of permitivity will be
View SolutionMatch the physical quantities given in column I with dimensions expressed interms of mass (M), length (L), time (T) and charge (Q) given in column II and wire the correct answer against the match quantity in labourar form.
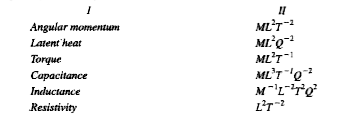
View SolutionThe dimension of B22μ0, where B is magnetic field and μ0 is the magnetic permeability of vacuum, is :
View SolutionThe dimensions of resistivity in terms of M, L, T and Q, where Q stands for the dimensions of charge is
View SolutionLet ε0 denote the dimensional formula of the permittivity of vacuum. If M= mass , L=length , T=time and A=electric current , then dimension of permittivity is given as [MpLqTrAs]. Find the value of p−q+rs
View Solution
