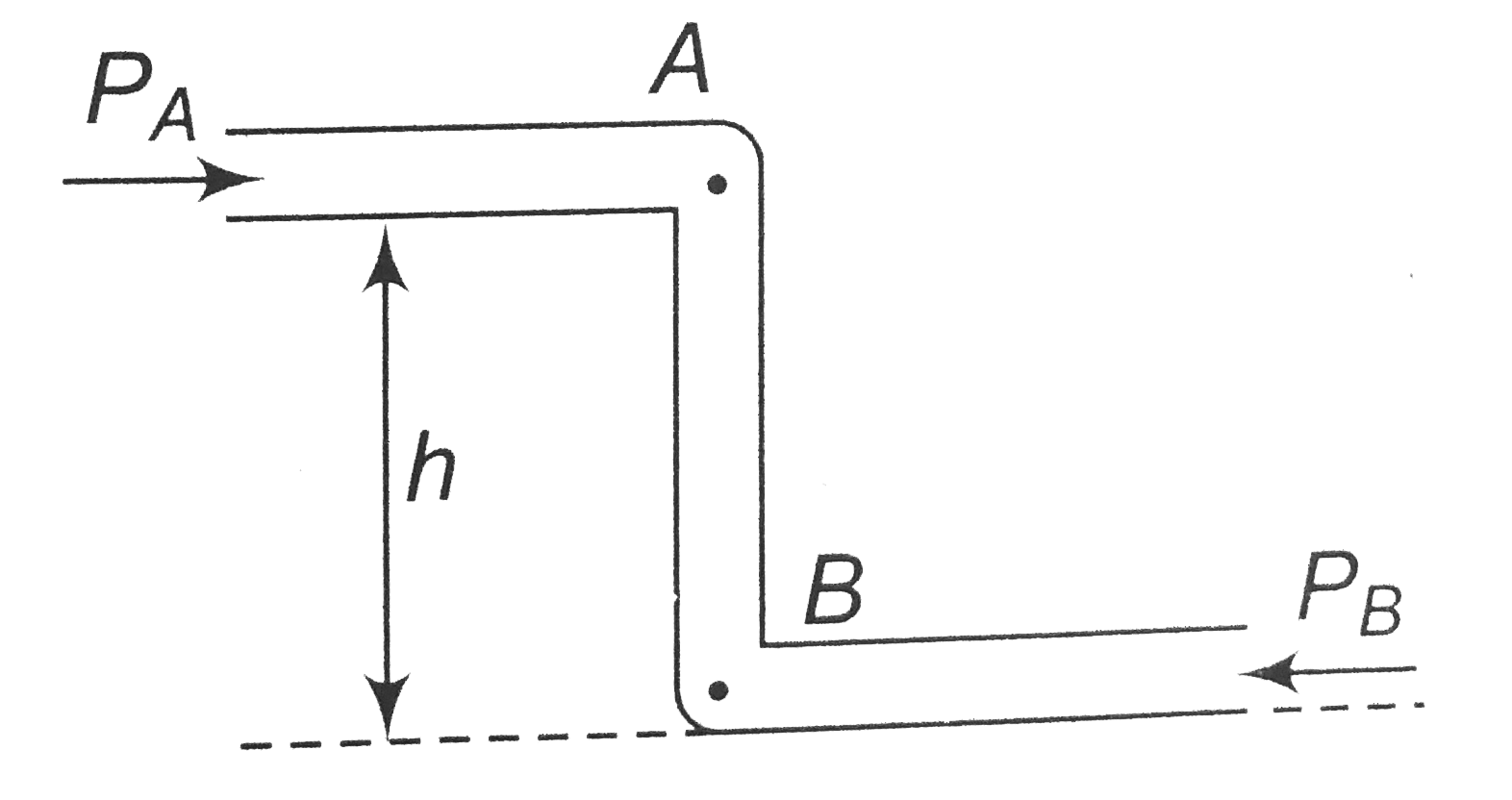
In this figure, an ideal liquid flows through the tube having uniform area of cross-section and is held in vertical plane. Find the ratio of speed of liquid at A and B and also find the pressure difference between- these points.

As area of cross-section is uniform therefore according to equation of continuity speed of liquid is same at all points
i.e. vA=vB
But during motion of liquid from A to B the potential energy decreases
∴ According to Bernoullis theorem
12v2+gh+Pρ =constant
⇒gh+PAρ=PBρ
⇒PB−PA=ρgh
Similar Questions
Knowledge Check
In the figure, an ideal liquid flows through the tube, which is of uniform cross section. The liquid has velocities vA and vB, and pressures PA and PB at the points A and B, respectively. Then
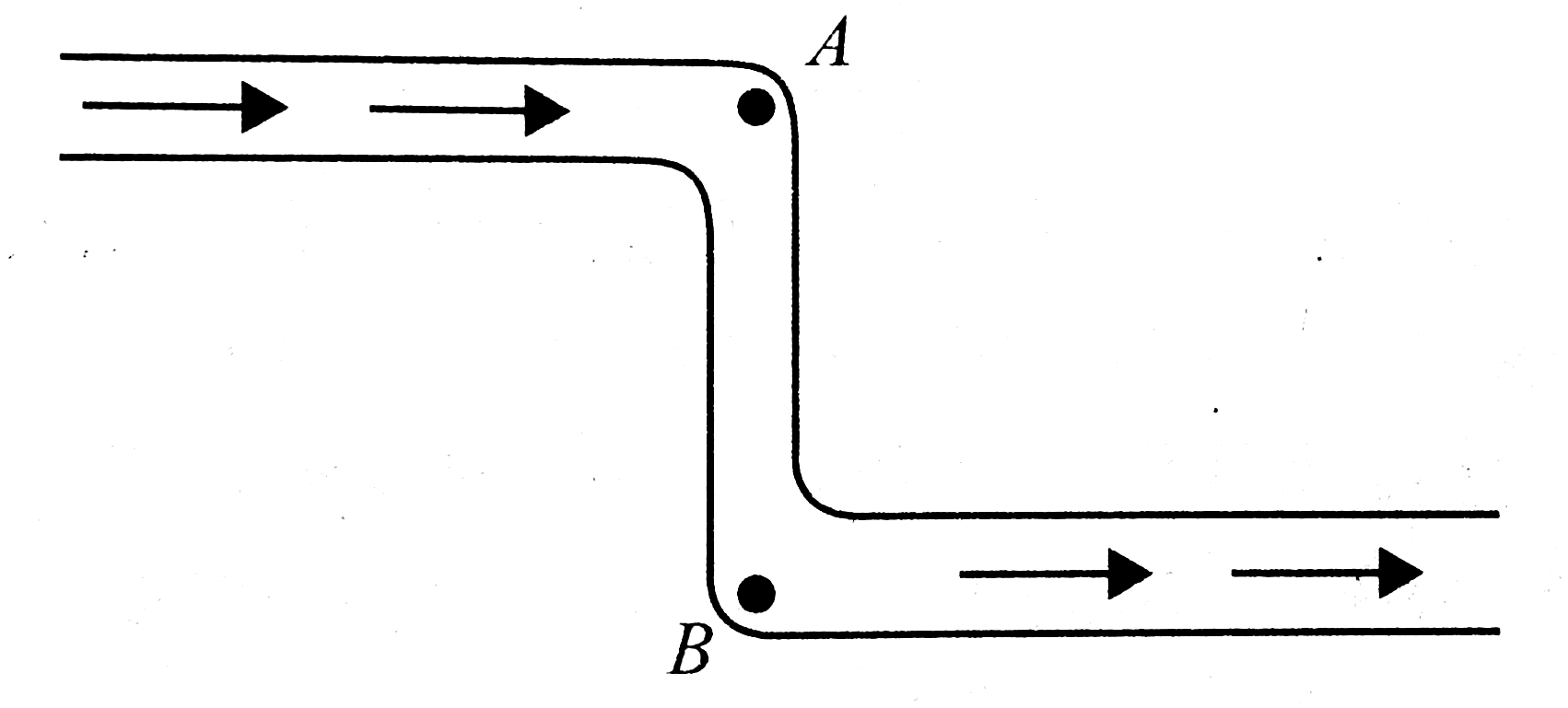 AvB>vABvB=vACPB<PADPB=PA
AvB>vABvB=vACPB<PADPB=PA
Figure shows a siphon. The liquid shown in water. The pressure difference PB−PA between the points A and B is

View SolutionFigure shows an ideal fluid flowing through a uniform cross-sectional tube in the vertical tube with liquid velocities vA and vB and pressure PA and PB. Knowing that offers no resistance to fluid flow then which of the following is true.
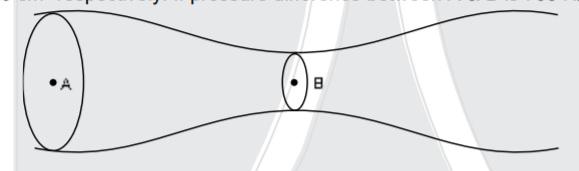
View SolutionAn ideal liquid (water) flowing through a tube of non-uniform cross section area at A and B are 40cm2 and 20cm2 respectively. If pressure difference between A & B is 700 Nm2 then volume flow rate is
View SolutionA viscous liquid flows through a horizontal pipe of varying cross-sectional area. Identify the option which correctly represents the variation of height of rise of liquid in each vertical tube
View SolutionA liquid flows through two capillary tubes A and B connected in series. The length and radius of B are twice that of A. What is the ratio of the pressure difference across A to that across B ?
View Solutionwater is flowing through a tube of non-uniform cross-section. If the radii of the tube at the entrance and the exit are in the ratio 3:2 then the ratio of the velocites of flow of watern at the entrance and the exit is
View SolutionA liquid is flowing through a pipe of non-uniform cross-section. At a point where area of cross-section of the pipe is less, match the following columns.

View Solution

