Figure shows a liquid flowing through a tube at the rate of 0.1m3/s. The tube is branched into two semicircular tubes of cross-sectional area A/3 and 2A/3. The velocity of liquid at Q is (the cross section of the main tube is A=10−2m2 and vp=20m/s)

5m/s
30m/s
35m/s
none of these
The correct Answer is:A
From a equationof continuity
Rate =r=A3Vp+(A−A3)VQ
∴VP+2VQ=3rA=3×0.110−2=30m/s
As VP+2VQ=5m/s
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Flow rate of blood through a capillary of cross - sectional are of 0.25m2 is 100cm3/s. The velocity of flow of blood iis
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
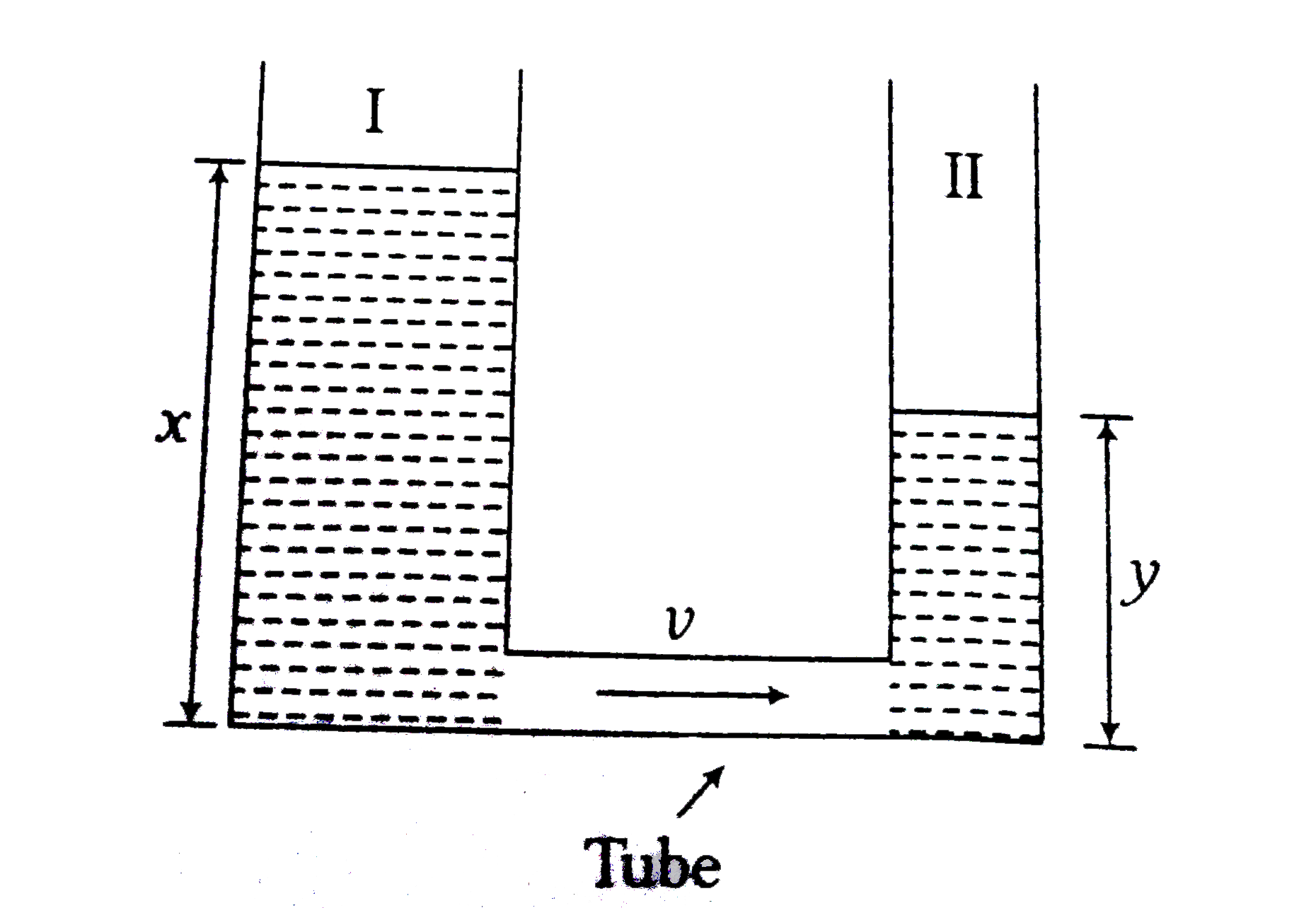
View Solution
Knowledge Check
A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The differnece in the levels of the liquid in the two vertical tubes is h. then
 Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=ghTwo capillary tubes of radii 0.2 cm and 0.4 cm are dipped in the same liquid.The ratio of heights through which liquid will rise in the tube is
A1:2B2:1C1:4D4:1
A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then
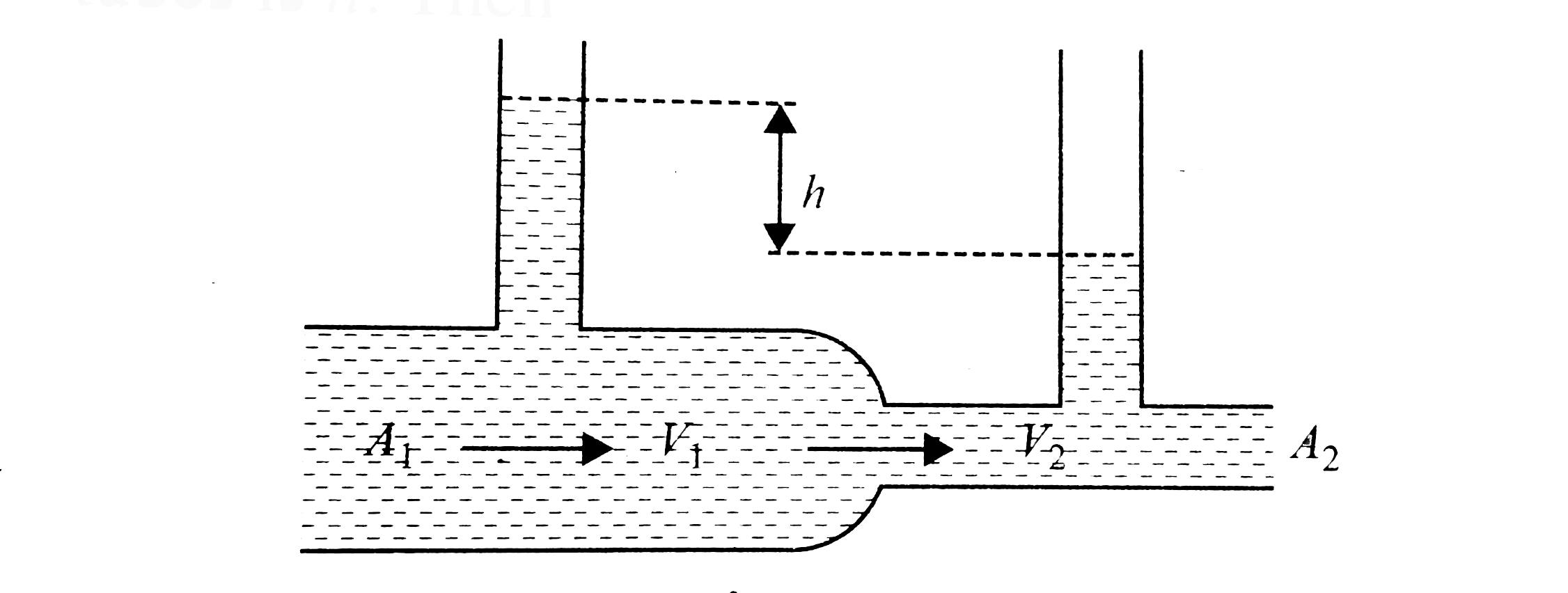
View Solution(a) What is meant by the principle of continuity ? Show that velocity of a liquid is inversely proportional to the area of cross-section of a pipe or tube.
View Solutionwater is flowing through a tube of non-uniform cross-section. If the radii of the tube at the entrance and the exit are in the ratio 3:2 then the ratio of the velocites of flow of watern at the entrance and the exit is
View SolutionThe water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionWater is flowing steadily through a horizontal pipe of non - uniform cross - section . If the velocity of water cross - section is 0.02m2 is 2m/s , what is the velocity of water at another point where the cross - section is 0.01m2 ?
View SolutionAn incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity 'v' of the fluid is:

View Solution
