An ideal fluid flows in the pipe as shown in the figure. The pressure in the fluid at the bottom is the same as it is at the top . If the velocity of the top . Then the ratio of areas , is

The correct Answer is:B
Using equation of continuity we have
From Bernoulli's theorem
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A horizontal pipe of varying cross-sectional area carries water flowing at a constant rate. The pressure at sections (1) and (2) are 50cm and 20cm of Hg. If the velocity of section (1) is 5m/s, what is the velocity of section (2). Also determine the ratio of areas at sections (1) and (2) (as shown in Fig.
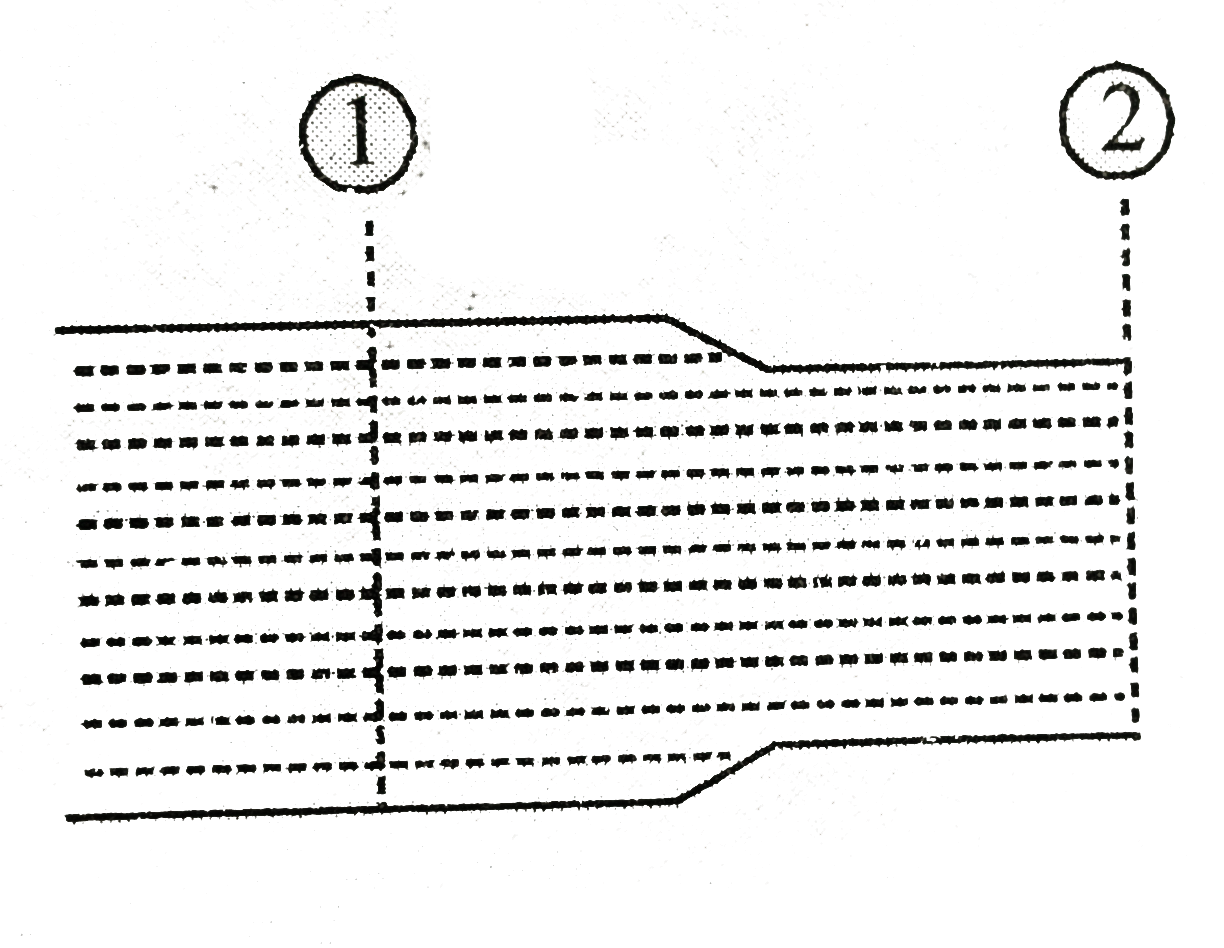
View SolutionAn ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
View Solution
Knowledge Check
The pressure P1 at the top of a dam and P2 at a depth h from the top inside water (density ρ) are related as :
AP1>P2BP1=P2CP1−P2=hρgDP2−P1=hρgAn ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
A9:4B3:2C√3:√2D√2:√3An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
A9:4B3:2C√3:√2D√2:√3
A liquid flows in a tube from left to right as shown in figure. A1 and A2 are the cross-section of the portions of the tube as shown. Then the ratio of speeds v1/v2 will be

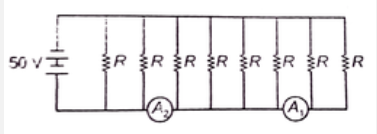
View SolutionIn the situation shown , the readings of ideal ammeters A1 and A2 are in the ratio.
View SolutionAn ideal fluid flows through a pipe of circular cross - section with diameters 5 cm and 10 cm as shown in the figure. The ratio of velocities of fluid at A and B is

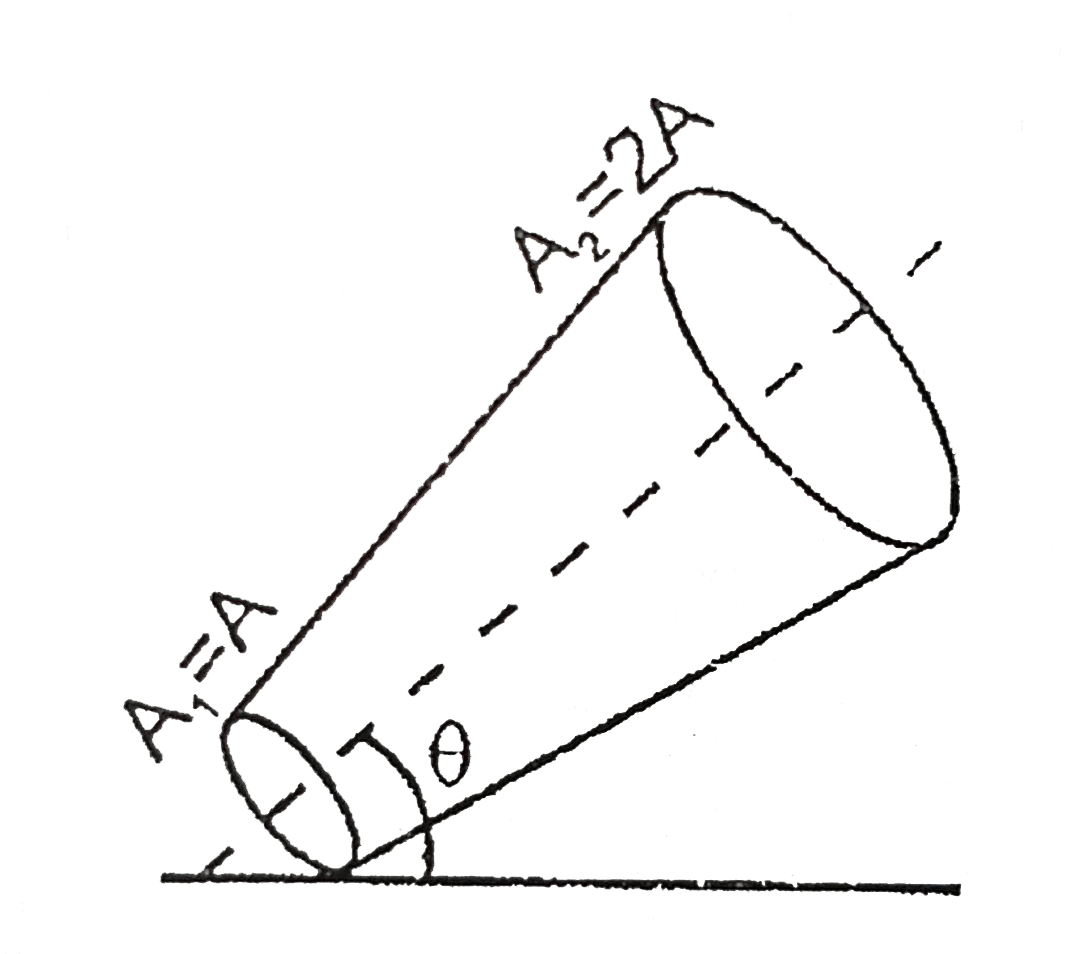
View SolutionA portion of a tube is shown in the figure. Fluid is flowing from cross-section area A1 to A2. The two cross-sections are at distance 'l' from each other. The velocity of the fluid at section A2 is √gl2. If the pressures at A1 & A2 are same, then the angle made by the tube with the horizontal will be:
View SolutionA liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The differnece in the levels of the liquid in the two vertical tubes is h. then

View Solution
