A liquid of density 900 kg/m3 is filled in a cylindrical tank open from top of upper radius 0.9 m and lower radius 0.3 m. A capillary tube of length l is attached at the bottom of the tank as shown in the figure. The capillary has outer radius 0.002 m and inner radius a.
When pressure p is applied at the top of the tank volume flow rate of the liquid is 8×10−6m3/s and if capillary tube is detached, the liquid comes out from the tank with a velocity 10 m/s
[Given : πa2=10−6m2anda2/1=2×10−6m]
Determine the coefficient of viscosity in SI units when the capillary tube is attached :
![A liquid of density 900 kg//m^3 is filled in a cylindrical tank open from top of upper radius 0.9 m and lower radius 0.3 m. A capillary tube of length l is attached at the bottom of the tank as shown in the figure. The capillary has outer radius 0.002 m and inner radius a. When pressure p is applied at the top of the tank volume flow rate of the liquid is 8 xx 10 ^(-6 ) m^3// s and if capillary tube is detached, the liquid comes out from the tank with a velocity 10 m/s [Given : pi a ^2 = 10 ^(-6) m^ 2 and a ^ 2//1 = 2 xx 10 ^(-6) m ] Determine the coefficient of viscosity in SI units when the capillary tube is attached :](https://d10lpgp6xz60nq.cloudfront.net/physics_images/VMC_PHY_XI_WOR_BOK_02_C08_E05_031_Q01.png)
1720
1360
1800
190
The correct Answer is:A
By Poiseuille’s equation, the rate of flow of liquid in the capillary tube Q=π(Δp)a48η1
∴8×10−6=(πa2)(Δp)8η(a21) ∴η=(πa2)(Δp)(a21)8×8×10−6
Substituting the values, we have η=(10−6)(49×105)(2×10−6)8×8×10−6=1720N−s/m2
Topper's Solved these Questions
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )
31 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
Similar Questions
A thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is
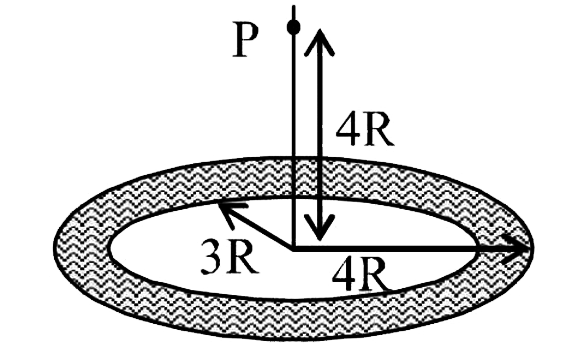
View SolutionA thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is

View Solution_E01_290_Q01.png)
Shown in the figure is a container whose top and bottom diameters are D and d respectively At the bottom of the container these is a cappillary tube of outer radius b and inner radius a. the volume flow rate in the capillary is Q. if the capillary is removed the liquid comes out with a velocity of v0. The density of the liquid is given as calculate the coefficient of viscosity η (given πa2=10−6m2 and a2l=2×10−6m]
View SolutionA tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
View SolutionFigure shows a capillary tube of radius r dipped into water. If the atmosphere pressure is P0, the pressure at point A is
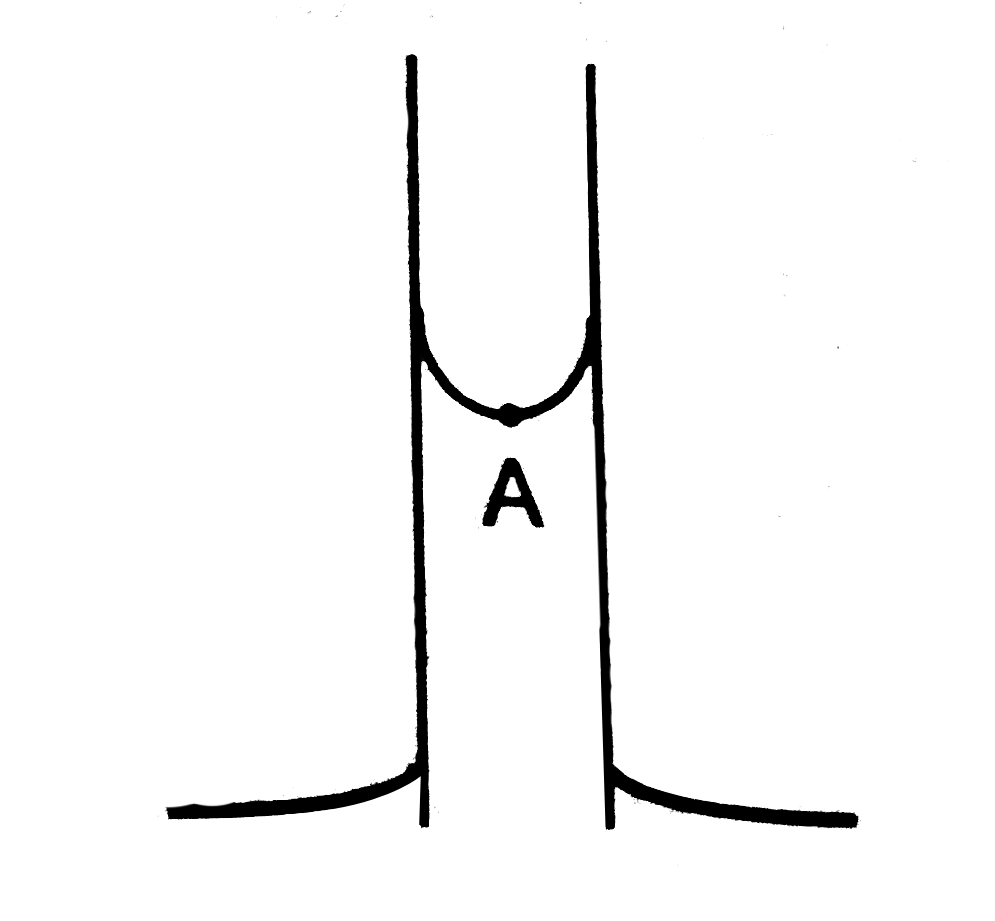
View SolutionA capillary tube of the radius r is immersed in water and water rise in it to a height H. Mass of water in the capillary tube is m. If the capillary of radius 2r is taken and dipped in water, the mass of water that will rise in the capillary tube will be
View SolutionA capillary tube of radius R is immersed in water and water rises in it to a height H . Mass of water in the capillary tube is . M If the radius of the tube is doubled, mass of water that will rise in the capillary tube will now be
View SolutionA capillary tube of radius R is immersed in water and water rises in it to a height H . Mass of water in the capillary tube is . M If the radius of the tube is doubled, mass of water that will rise in the capillary tube will now be
View SolutionIf a capillary tube of radius 1 mm is immersed in water , the mass of water rising in the capillary tube is M . If the radius tube is doubled , then the mass of water , that rises in the capillary tube will be
View SolutionA circular running track has inner radius 126 m and outer radius 140 m . Find the area of the track .
View Solution
