A tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
1.85g(wt)cm2
89.25g(wt)cm2
462.5g(wt)cm2
500g(wt)cm2
The correct Answer is:C
To find the pressure at the bottom of the tank filled with water and oil, we can follow these steps:
Step 1: Understand the setup
The tank has a total height of 5 meters. It is half-filled with water and then topped off with oil. The density of the oil is given as 0.85g/cm3.
Step 2: Determine the heights of the liquids
Since the tank is 5 meters high and half-filled with water, the height of the water column (h1) is:
h1=52=2.5m
The height of the oil column (h2) is also:
h2=5−2.5=2.5m
Step 3: Convert the density of oil to SI units
The density of oil is given as 0.85g/cm3. To convert this to SI units (kg/m³):
ρoil=0.85g/cm3=0.85×1000kg/m3=850kg/m3
Step 4: Use the formula for pressure
The pressure at the bottom of the tank (P) is given by:
P=P0+Pwater+Poil
Where:
- P0 is the atmospheric pressure (approximately 105Pa),
- Pwater=ρwater⋅g⋅h1,
- Poil=ρoil⋅g⋅h2.
Step 5: Calculate the pressures due to water and oil
The density of water (ρwater) is 1000kg/m3 and g (acceleration due to gravity) is approximately 9.81m/s2.
Calculating the pressure due to water:
Pwater=ρwater⋅g⋅h1=1000⋅9.81⋅2.5=24525Pa
Calculating the pressure due to oil:
Poil=ρoil⋅g⋅h2=850⋅9.81⋅2.5=20896.25Pa
Step 6: Calculate total pressure at the bottom of the tank
Now, substituting the values into the pressure formula:
P=P0+Pwater+Poil=105+24525+20896.25
Calculating this gives:
P=100000+24525+20896.25=145421.25Pa
Step 7: Convert to more convenient units if needed
If we want to express this pressure in terms of grams per square centimeter:
P=145421.25Pa9.81m/s2≈14800g/cm2
Final Answer
The pressure at the bottom of the tank due to the liquids is approximately 145421.25Pa or 14800g/cm2.
---
The tank has a total height of 5 meters. It is half-filled with water and then topped off with oil. The density of the oil is given as 0.85g/cm3.
Since the tank is 5 meters high and half-filled with water, the height of the water column (h1) is:
h1=52=2.5m
The height of the oil column (h2) is also:
h2=5−2.5=2.5m
The density of oil is given as 0.85g/cm3. To convert this to SI units (kg/m³):
ρoil=0.85g/cm3=0.85×1000kg/m3=850kg/m3
The pressure at the bottom of the tank (P) is given by:
P=P0+Pwater+Poil
Where:
- P0 is the atmospheric pressure (approximately 105Pa),
- Pwater=ρwater⋅g⋅h1,
- Poil=ρoil⋅g⋅h2.
The density of water (ρwater) is 1000kg/m3 and g (acceleration due to gravity) is approximately 9.81m/s2.
Pwater=ρwater⋅g⋅h1=1000⋅9.81⋅2.5=24525Pa
Poil=ρoil⋅g⋅h2=850⋅9.81⋅2.5=20896.25Pa
Now, substituting the values into the pressure formula:
P=P0+Pwater+Poil=105+24525+20896.25
Calculating this gives:
P=100000+24525+20896.25=145421.25Pa
If we want to express this pressure in terms of grams per square centimeter:
P=145421.25Pa9.81m/s2≈14800g/cm2
The pressure at the bottom of the tank due to the liquids is approximately 145421.25Pa or 14800g/cm2.
Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Properties of Matter & Fluid Mechanics)(Surface Tension)
Explore 26 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Thermal Physics) (Temperature scales & thermal expansion)
Explore 13 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Properties of Matter & Fluid Mechanics)(Fluid Dynamics + Viscosity)
Explore 18 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
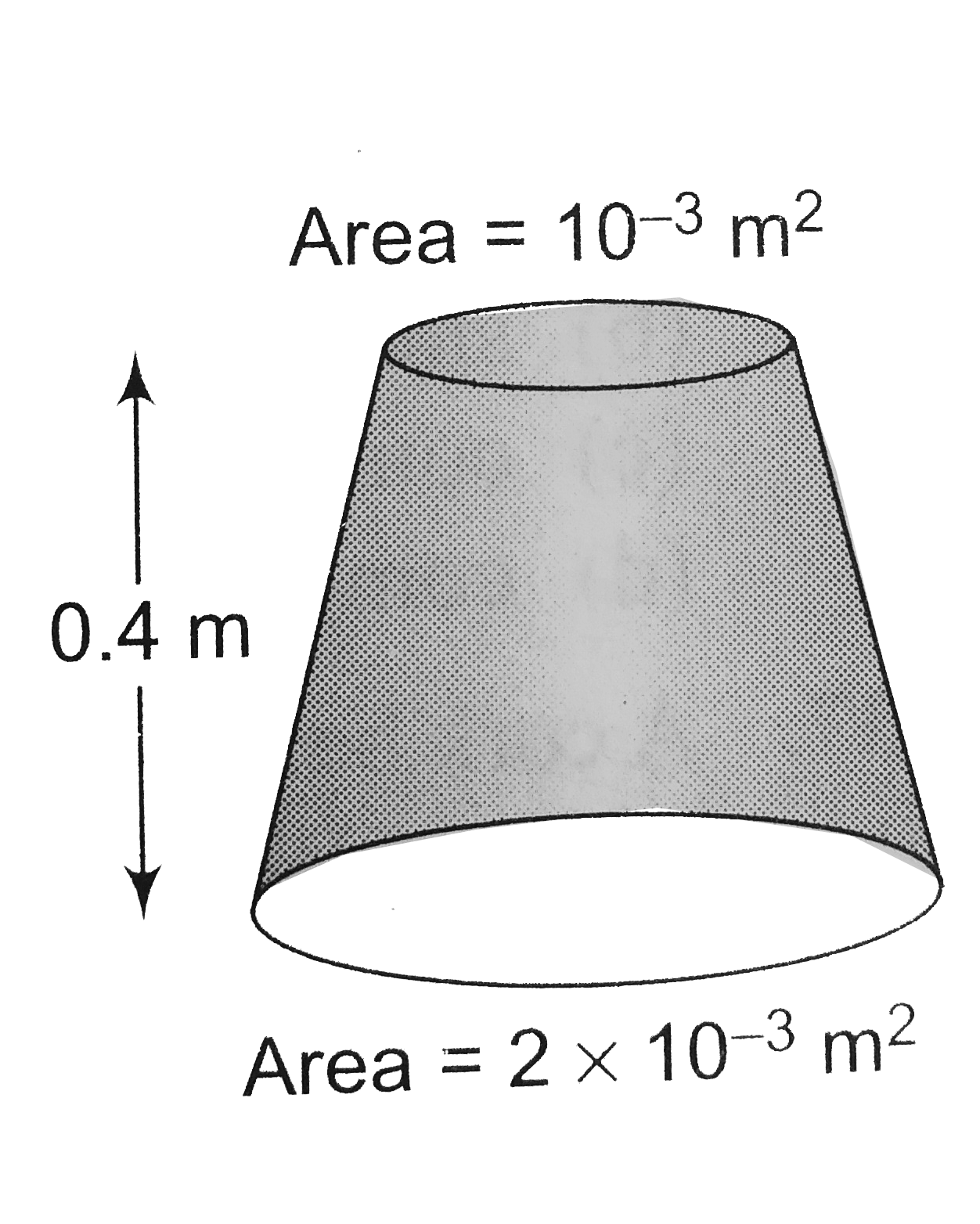
A uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
View SolutionA hole is made at the bottom of the tank filled with water (density =1000kgm−3). If the total pressure at the bottom of the tank is three atmospheres (1 atmosphere =105Nm−2), then the velocity of efflux is nearest to
View SolutionA water tank is 20 m deep . If the water barometer reads 10 m at the surface , then what is the pressure at the bottom of the tank in atmosphere ?
View SolutionP is the atmospheric pressure and the pressure at the bottom of a tank of water is 3P. If the water is drawn out to lower the level of water by one fifth, then the pressure at the bottom of the tank will be
View SolutionA tank of height H and base area A is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area A3 and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
After long time, when the height of water inside the tank again becomes equal to H2, the solid cylinder is taken out. then the velocity of liquid flowing out of the orifice (just after removing the cylinder) will be
View SolutionA tank is filled with water of density 103kg/m3 and oil of density 0.9×103kg/m3.The height of water layer is 1m and that of the oil layer is 4M. The velocity of efflux front an opening in the bottom of the tank is
View SolutionThe pressure at the bottom of a water tank is 4 P, where P is .atmospheric pressure. If water is drawn out till the water level decreases by —35th, then pressure at the bottom of the tank is
View SolutionA tank of large base area is filled with water up to a height of 5m. A hole of 2cm2 cross section in the bottom allows the water to drain out in continuous streams. For this situation, mark out the correct statement(s) (take ρwater=1000kg/m3,g=10ms−12)

View SolutionThe flat bottom of cylinder tank is silvered and water (μ=43) is filled in the tank upto a height h. A small bird is hovering at a height 3h from the bottom of the tank. When a small hole is opened near the bottom of the tank, the water level falls at the rate of 1 cm/s. The bird will perceive that his velocity of image is 1/x cm/sec (in downward directions) where x is
View SolutionIf liquid of density ρ is filled in an open cylindrical container to height h, then pressure at bottom
View Solution

