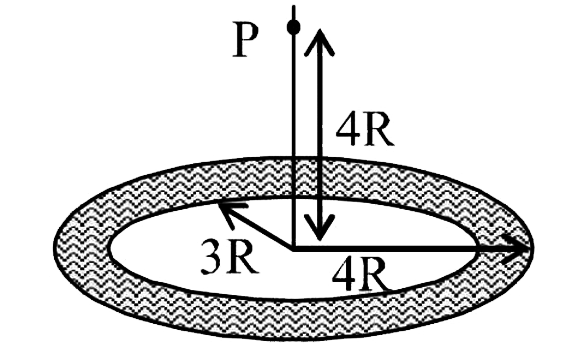
A thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is
2GM7R(4√2−5)
−2GM7R(4√2−5)
GM4R
2GM5R(√2−1)
The correct Answer is:A
Work required to take unit mass from infinity to point P =VP br> ∴ Work required to take it from P to infinity =−VP
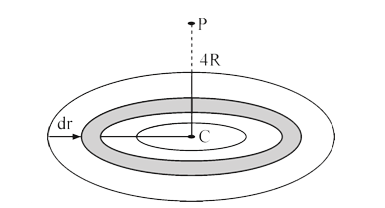
To calculate VP , consider a ring element of radius r and width dr . Gravitational potential due to this ring at P is :
dVP=−G(dm)√r2+(4R)2=−G√r2+16R2M(2prdr)(16pR2−9pR2)=−2GM7R2rdr√r2+16R2
∴VP=∫dVP=−2GM7R2∫4R3Rrdr√r2+16R2
Let r2+16R2=t2⇒2rdrdt=2t⇒rdr=tdt
∴∫rdr√r2+16R2=∫tdt√t2=∫dt=t=√r2+16R2
∴VP=−2GM7R2[√r2+16R2]4R3R=−2GM7R2[√32R2−√25R2]
=−2GM7R(4√2−5)∴Wreqd=−VP=2GM7R(4√2−5)
Topper's Solved these Questions
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) MULTIPLE OPTIONS CORRECT TYPE
Explore 5 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive)ASSERTIOIN AND REASON
Explore 1 Video
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Main (Archive)
Explore 43 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
Similar Questions
For a uniform ring of mass M and radius R at its centre
View SolutionA thin annular disc of outer radius R and R2 inner radius has charge Q uniformly distributed over its surface. The disc rotates about its axis with a constant angular velocity ω. Choose the correct option(s):
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionA particle of mass m was transferred from the centre of the base of a uniform hemisphere of mass M and radius R into infinity.
What work was performed in the process by the gravitational force exerted on the particle by the hemisphere?
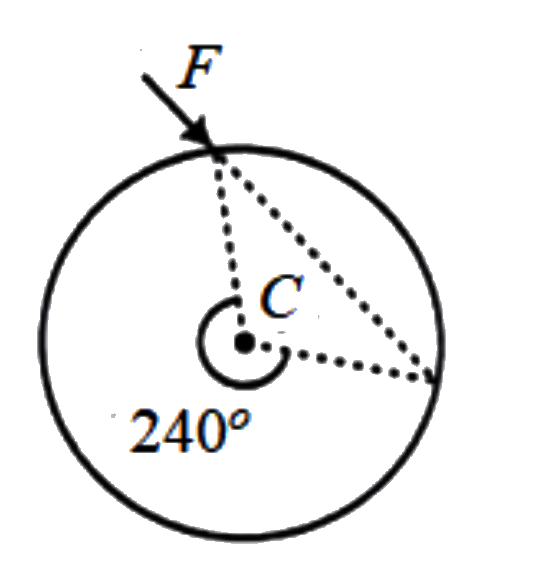
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
View SolutionConsider a thin uniform spherical layer of mass M and radius R. The potential energy of gravitational interaction of matter forming this shell is :
View SolutionThe moment of inertia of hollow sphere (mass M) of inner radius R and outer radius 2R, having material of uniform density, about a diametric axis is
View SolutionA uniform disc of mass m and radius r and a point mass m are arranged as shown in the figure. The acceleration of point mass is :( Assume there is no slipping between pulley and thread and the disc can rotate smoothly about a fixed horizontal axis passing through its centre and perpendicular to its plane )

View SolutionA uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.

View Solution
