Consider a spherical gaseous cloud of mass density ρ(r) in a free space where r is the radial distance from its centre. The gaseous cloud is made of particle of equal mass m moving in circular orbits about their common centre with the same kinetic energy K. The force acting on the particles is their mutual gravitational force. If ρ(r) is constant with time. the particle number density n(r)=ρ(r) /m is : (g =universal gravitational constant)
3Kπr2m2G
K2πr2m2G
K6πr2m2G
Kπr2m2G
The correct Answer is:B
To solve the problem, we need to find the particle number density n(r) given the mass density ρ(r) of a spherical gaseous cloud. The steps to derive the solution are as follows:
Step 1: Understand the System
We have a spherical gaseous cloud with a mass density ρ(r) that is constant over time. The particles of mass m are moving in circular orbits around their common center with the same kinetic energy K.
Step 2: Relate Gravitational Force and Centripetal Force
For a particle in circular motion, the gravitational force acting on it must equal the centripetal force required to keep it in that motion. The gravitational force Fg acting on a particle of mass m at a distance r from the center is given by:
Fg=GM(r)mr2
where M(r) is the mass enclosed within radius r, and G is the universal gravitational constant.
The centripetal force Fc required for circular motion is given by:
Fc=mv2r
where v is the speed of the particle.
Step 3: Equate the Forces
Setting the gravitational force equal to the centripetal force gives us:
GM(r)mr2=mv2r
We can cancel m from both sides (assuming m≠0):
GM(r)r2=v2r
Step 4: Express Mass M(r)
Rearranging the equation gives:
M(r)=v2rG
Step 5: Relate Kinetic Energy to Speed
The kinetic energy K of the particles is given by:
K=12mv2
From this, we can express v2:
v2=2Km
Step 6: Substitute v2 into M(r)
Substituting v2 into the expression for M(r):
M(r)=2KrGm
Step 7: Find the Elemental Mass dm
The elemental mass dm of a spherical shell of thickness dr at radius r can be expressed in terms of density:
dm=ρ(r)dV=ρ(r)(4πr2dr)
Step 8: Relate dm to M(r)
We can express the total mass M(r) as the integral of dm:
M(r)=∫r0dm=∫r0ρ(r′)(4πr′2)dr′
Assuming ρ(r) is constant, we can simplify this to:
M(r)=ρ⋅43πr3
Step 9: Equate the Two Expressions for M(r)
Now we have two expressions for M(r):
1. M(r)=2KrGm
2. M(r)=ρ⋅43πr3
Setting them equal gives:
2KrGm=ρ⋅43πr3
Step 10: Solve for ρ
Rearranging this equation to solve for ρ:
ρ=2KGm⋅34πr2
Step 11: Find Particle Number Density n(r)
The particle number density n(r) is given by:
n(r)=ρ(r)m
Substituting the expression for ρ:
n(r)=2KGm2⋅34πr2
Final Result
Thus, the particle number density n(r) is:
n(r)=3K2πGm2r2
We have a spherical gaseous cloud with a mass density ρ(r) that is constant over time. The particles of mass m are moving in circular orbits around their common center with the same kinetic energy K.
For a particle in circular motion, the gravitational force acting on it must equal the centripetal force required to keep it in that motion. The gravitational force Fg acting on a particle of mass m at a distance r from the center is given by:
Setting the gravitational force equal to the centripetal force gives us:
Rearranging the equation gives:
The kinetic energy K of the particles is given by:
Substituting v2 into the expression for M(r):
The elemental mass dm of a spherical shell of thickness dr at radius r can be expressed in terms of density:
We can express the total mass M(r) as the integral of dm:
Now we have two expressions for M(r):
2. M(r)=ρ⋅43πr3
Rearranging this equation to solve for ρ:
The particle number density n(r) is given by:
Thus, the particle number density n(r) is:
Topper's Solved these Questions
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) MULTIPLE OPTIONS CORRECT TYPE
Explore 5 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive)ASSERTIOIN AND REASON
Explore 1 Video
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Main (Archive)
Explore 43 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
Similar Questions
A particle of mass m is rotating in a plane in circular path of radius r. Its angular momentum is L. The centripetal force acting on the particle is
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
View SolutionThree particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
View SolutionTwo particles of equal mass m0 are moving round a circle of radius r due to their mutual gravitational interaction. Find the time period of each particle.
View SolutionA paticle of mass m is executing uniform circular motion on a path of radius r. If p is the magnitude of its linear momentum, then the radial force acting on the particle is
View SolutionFour particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionFour similar particles of mass m are orbiting in a circle of radius r in the same direction and same speed because of their mutual gravitational attractive force as shown in the figure . Speed of a particle is given by
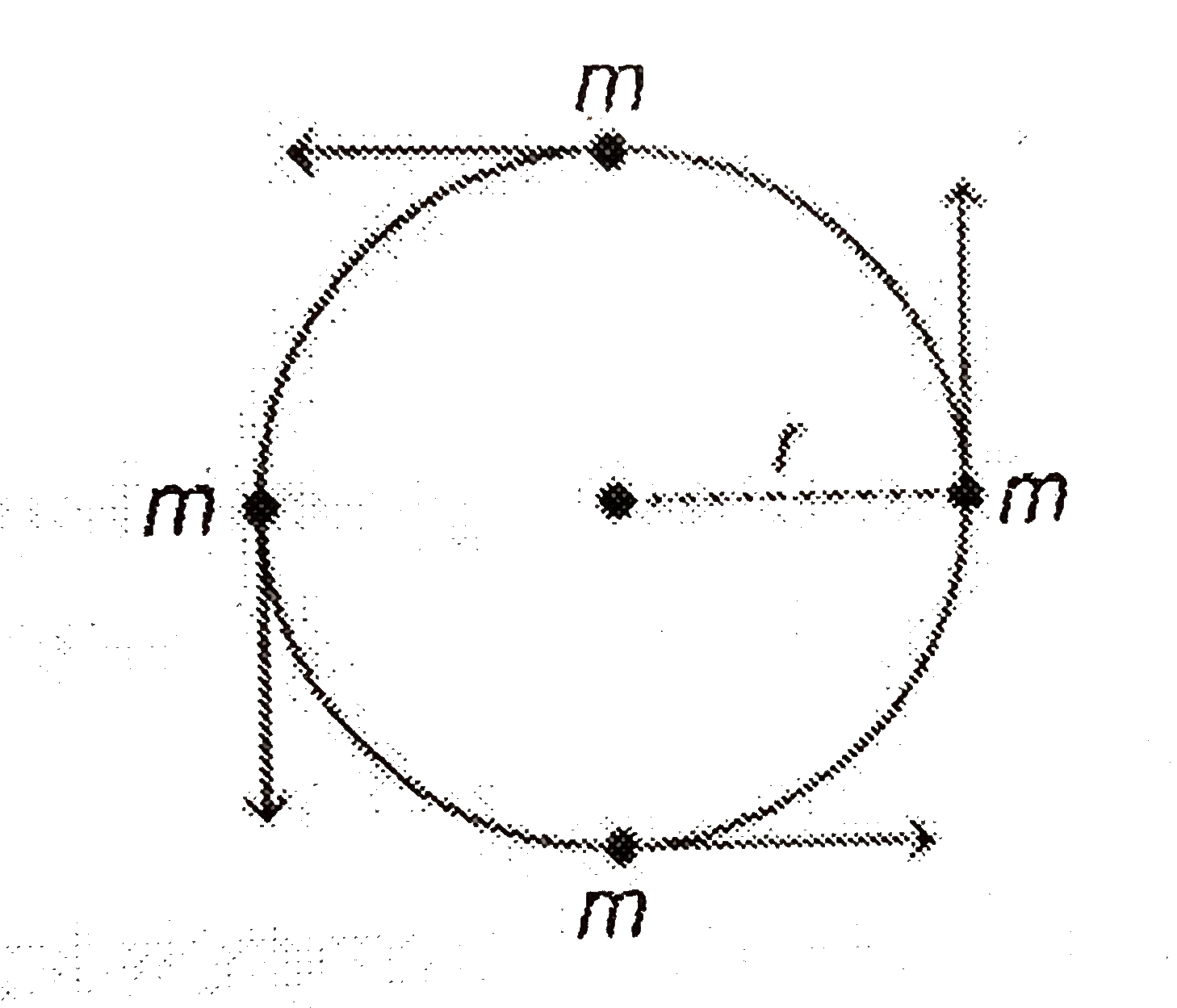
View SolutionFind the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View Solution