Water enters into a smooth horizontal tapering tube with a speed 2 m/sec and emerges out of the tube with a speed 8 m/sec . Find the ratio of the radii of cross sections of the tube at these two ends.
To solve the problem, we will use the principle of continuity in fluid mechanics, which states that the product of the cross-sectional area (A) and the velocity (V) of a fluid remains constant along a streamline.
1. Identify Given Values:
- Speed of water entering the tube (V1) = 2 m/s
- Speed of water emerging from the tube (V2) = 8 m/s
2. Apply the Equation of Continuity:
- According to the equation of continuity, we have:
A1V1=A2V2
- Where:
- A1 is the cross-sectional area at the entrance,
- A2 is the cross-sectional area at the exit.
3. Express Areas in Terms of Radii:
- The area of a circle is given by A=πr2. Therefore:
A1=πr21andA2=πr22
- Substituting these into the continuity equation gives:
πr21V1=πr22V2
- The π cancels out, leading to:
r21V1=r22V2
4. Rearranging for the Ratio of Areas:
- Rearranging the equation gives:
r21r22=V2V1
- Substituting the known velocities:
r21r22=82=4
5. Finding the Ratio of Radii:
- Taking the square root of both sides gives:
r1r2=√4=2
Final Answer:
The ratio of the radii of the cross sections of the tube at the two ends is:
r1r2=2
- Speed of water entering the tube (V1) = 2 m/s
- Speed of water emerging from the tube (V2) = 8 m/s
- According to the equation of continuity, we have:
A1V1=A2V2
- Where:
- A1 is the cross-sectional area at the entrance,
- A2 is the cross-sectional area at the exit.
- The area of a circle is given by A=πr2. Therefore:
A1=πr21andA2=πr22
- Substituting these into the continuity equation gives:
πr21V1=πr22V2
- The π cancels out, leading to:
r21V1=r22V2
- Rearranging the equation gives:
r21r22=V2V1
- Substituting the known velocities:
r21r22=82=4
- Taking the square root of both sides gives:
r1r2=√4=2
The ratio of the radii of the cross sections of the tube at the two ends is:
r1r2=2
Similar Questions
Water flows out of a big tank along a horizontal tube Ab of length L and radius R and bends at right angle at the other end as shown in the figure. Find moment of force exerted by water on the tube about the end A (Assume that the radius of the tube is small )
 View Solution
View SolutionA liquid can rise to a height of h in a capillary tube of length l (l>h). The tube filled with the liquid is kept horizontal with its two ends open. Now the tube is kept vertical with the liquid in it. Some liquid flows out. Find the height of the liquid remaining in the tube if the surface tension of the liquid is σ.
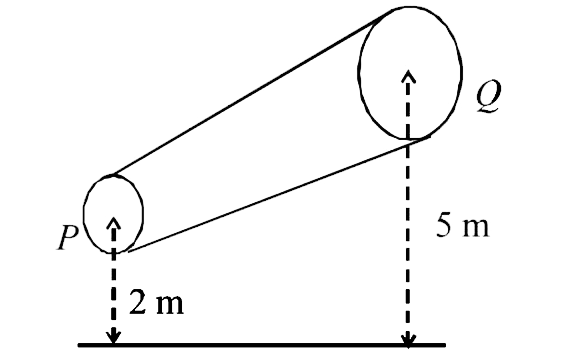
View SolutionA non-viscous liquid of constant density 1000kg/m3 flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two point P and Q at heights of 2 metres and 5 metres are respectively 4×10−3m2 and 8×10−3m2. The velocity of the liquid at point P is 1m/s. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q.
 View Solution
View SolutionWater is flowing through a tube of radius r with a speed v. If this tube is joined to another tube of radius r/2, what is the speed of water in the second tube?
View SolutionWater enters through end A with a speed v1 and leaves through end B with a speed v2 of cylindrical tube AB. The tube is always completely filled with water. In case I the tube is horizontal, in case II it vertical with the end A upward and in case III it is vertical with the end B upward. We have v1=v2for
View SolutionWater flows through a horizontal tube as shown in figure. If the difference of heights of water colun in the vertical tubes is 2 cm and the area of cross section at A and B are 4cm2and2cm2 respectively, find the rate of flow of water across any section.
 View Solution
View SolutionA cylindrical tube with a frictionless piston ends in a small hole of area of cross–section 2×10−6m2, which is very small as compared to the area of cross-section of the tube. The tube is filled with a liquid of density 104kg/m3. The tube is held horizontal and the piston is pushed at a constant speed so that liquid comes out of the hole at a constant rate 'Q'm3/s. No liquid leaks around the piston. The material of the tube can bear a maximum pressure 6×105 Pa. The maximum possible value of Q so that the tube does not break is __________ ×10−5m3/s. [Atmospheric pressure =105 Pa]
 View Solution
View SolutionA piston of a syringe pushes a liquid with a speed of 1 cm, / sec . The radii of the syring tube and the needle are R = 1 cm and r = 0.5 mm respectively . The velocity of the liquid coming out of the needle is
 View Solution
View SolutionThe thickness of a metallic tube is 1cm and the inner diameter of the tube is 12cm. Find the mass of 1m long tube, if the density of the metal be 7.8 gm/cm3
View SolutionThe thickness of a metallic tube is 1cm and the inner diameter of the tube is 12cm. Find the mass of 1m long tube, if the density of the metal be 7.8 gm/cm3
View Solution
