A liquid can rise to a height of h in a capillary tube of length l (l>h). The tube filled with the liquid is kept horizontal with its two ends open. Now the tube is kept vertical with the liquid in it. Some liquid flows out. Find the height of the liquid remaining in the tube if the surface tension of the liquid is σ.
To solve the problem, we need to analyze the situation of a liquid in a capillary tube when it is kept vertical after initially being horizontal. The liquid rises to a height h due to capillary action, and we need to find the height of the liquid remaining in the tube after some of it flows out.
1. Understand the Initial Conditions:
- The liquid can rise to a height h in a capillary tube of length l when it is horizontal.
- The tube is then kept vertical, and some liquid flows out.
2. Identify the Points of Interest:
- Let’s denote the points in the tube as follows:
- Point A: Just inside the top of the tube.
- Point B: Just inside the bottom of the tube.
- Point C: The liquid level in the tube after some has flowed out.
- Point D: The bottom of the tube.
3. Apply Pressure Balance:
- The pressure at point A (top) must equal the pressure at point D (bottom) when the liquid stops flowing out.
- The pressure at point A is atmospheric pressure PA.
- The pressure at point D can be expressed as:
PD=P−2σr−2σr
- Here, P is the atmospheric pressure, and 2σr accounts for the pressure drop due to surface tension at both the top and bottom surfaces of the liquid column.
4. Relate Pressures to the Height of the Liquid:
- The pressure at point C, which is at height h′ (the new height of the liquid after some has flowed out), is given by:
PC=PD+ρgh′
- Setting PA=PD, we can write:
P=P−4σr+ρgh′
- Simplifying this gives:
ρgh′=4σr
5. Relate to Initial Height:
- From capillary action, we know that the height h can also be expressed as:
h=2σρgr
- Substituting this into our previous equation:
ρgh′=2⋅2σr
- This implies:
h′=2h
6. Final Result:
- Therefore, the height of the liquid remaining in the tube after some has flowed out is:
h′=2h
Final Answer:
The height of the liquid remaining in the tube is 2h.
- The liquid can rise to a height h in a capillary tube of length l when it is horizontal.
- The tube is then kept vertical, and some liquid flows out.
- Let’s denote the points in the tube as follows:
- Point A: Just inside the top of the tube.
- Point B: Just inside the bottom of the tube.
- Point C: The liquid level in the tube after some has flowed out.
- Point D: The bottom of the tube.
- The pressure at point A (top) must equal the pressure at point D (bottom) when the liquid stops flowing out.
- The pressure at point A is atmospheric pressure PA.
- The pressure at point D can be expressed as:
PD=P−2σr−2σr
- Here, P is the atmospheric pressure, and 2σr accounts for the pressure drop due to surface tension at both the top and bottom surfaces of the liquid column.
- The pressure at point C, which is at height h′ (the new height of the liquid after some has flowed out), is given by:
PC=PD+ρgh′
- Setting PA=PD, we can write:
P=P−4σr+ρgh′
- Simplifying this gives:
ρgh′=4σr
- From capillary action, we know that the height h can also be expressed as:
h=2σρgr
- Substituting this into our previous equation:
ρgh′=2⋅2σr
- This implies:
h′=2h
- Therefore, the height of the liquid remaining in the tube after some has flowed out is:
h′=2h
The height of the liquid remaining in the tube is 2h.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 3 (SOLVED EXAMPLES)
31 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 (SOLVED EXAMPLES)
11 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
Similar Questions
Knowledge Check
When a capillary tube is dipped in a liquid, the liquid rises to a height H in the tube. The free liquid surface inside the tube is hemispherical in shape. The tube is now pushed down sothat the height of the tube outside the liquid is less than H. Then the
Aliquid will come out of the tube like in a small fountainBliquid will ooze out of the tube slowlyCfree liquid surface inside the tube is hemisphericalDthe liquid will fill the tube but not come out its upper end.When two capillary tubes of different diameters are dipped vertically, the rise of the liquids is
Asame in both the tubesBmore in tube of larger diameterCless in tube of smaller diameterDmore in the tube of smaller diameter
A liquid rises in a capillary tube when the angle of contact is:
View SolutionIn the glass capillary tube, the shape of the surface of the liquid depends upon
View SolutionFind time period of liquid column of length l in the shown tube.

View SolutionWater rises to a height h in a capillary tube lowered vertically into water to a depth l as shown in the figure. The lower end of the tube is now closed, the tube is the taken out of the water and opened again. The length of the water column remaining in the tube will be
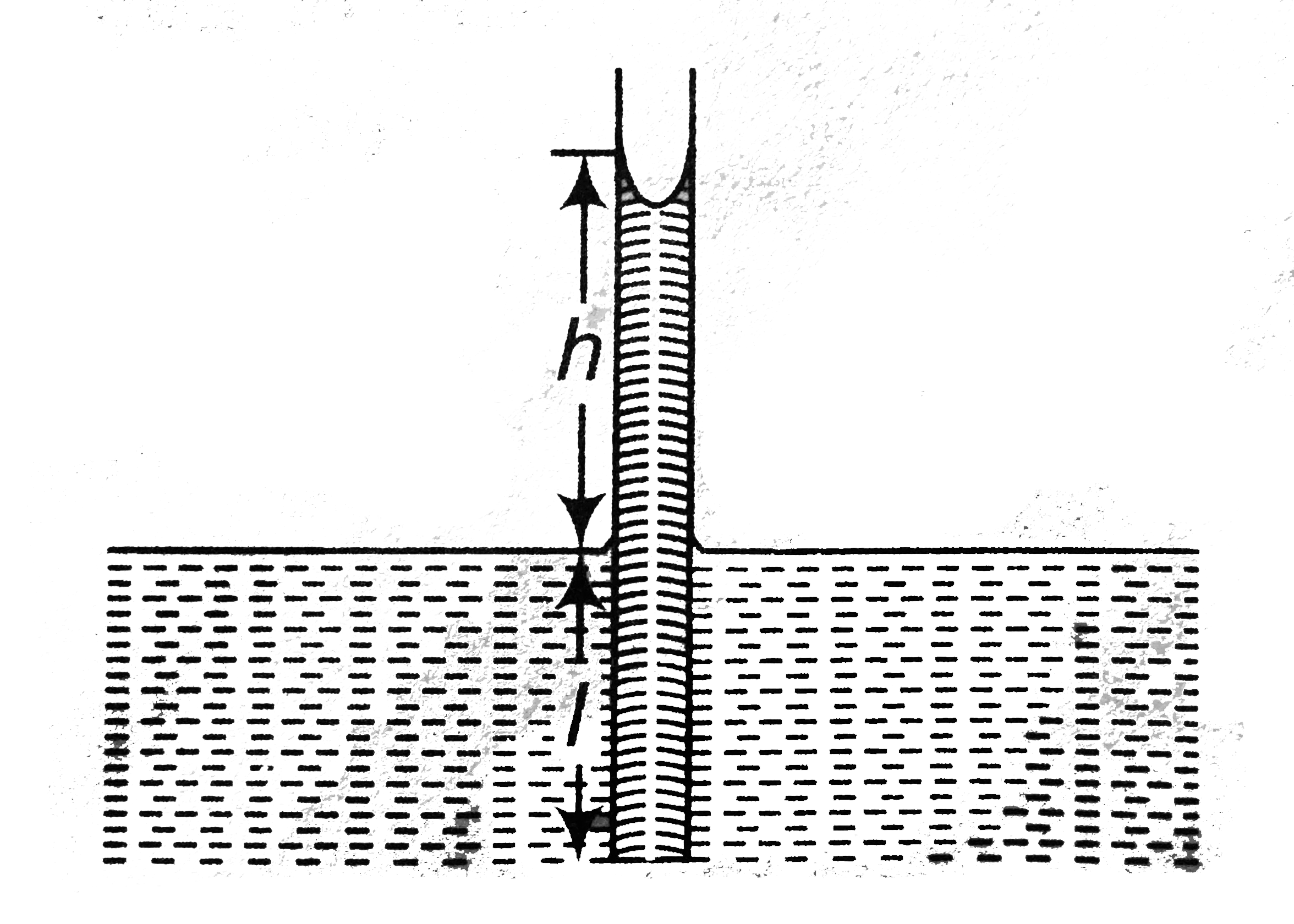 .
.
View SolutionA U-tube containing a liquid is accelerated horizontally with a constant acceleration a0. If the separation between the vertical limbs is l find the difference in the heights of the liquid in the two arms.
View SolutionA tube of conical bore is dipped into water with apex upwards. The length of the tube is 20cm and radii at the upper and lower ends are 0.1 and 0.3 cm. Find the height to which the liquid rises in the tube ( Surface tension of water = 80 dyne / cm ).
View Solution
