A rod of length L, cross sectional area A and density is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density . Find the period of small oscillations.
To find the period of small oscillations of the system described, we can follow these steps:
Step 1: Understand the System
We have a rod of length L, cross-sectional area A, and density ρ hanging from a rigid support via a spring with stiffness k. A small sphere of mass m is attached at the bottom of the rod, and the rod is partially immersed in a liquid of density ρliquid.
Step 2: Determine the Forces Acting on the System
When the rod is displaced downward by a small distance x, two forces will act on it:
1. Buoyant Force: The increase in buoyant force when the rod is displaced by x is given by:
Fbuoyant=ρliquid⋅g⋅Vdisplaced=ρliquid⋅g⋅(A⋅x)
where Vdisplaced=A⋅x is the volume of the rod that is now submerged.
2. Spring Force: The increase in spring force due to the displacement x is given by:
Fspring=k⋅x
Step 3: Net Force on the System
The net force F acting on the system when displaced by x is the sum of the buoyant force and the spring force:
F=Fbuoyant−Fspring=ρliquid⋅g⋅(A⋅x)−k⋅x
This can be simplified to:
F=(ρliquid⋅g⋅A−k)⋅x
Step 4: Apply Newton's Second Law
According to Newton's second law, the net force is also equal to the mass times acceleration:
F=mtotal⋅a
where mtotal is the total mass of the system. The total mass includes the mass of the rod and the mass of the sphere:
mtotal=ρ⋅A⋅L+m
Step 5: Equation of Motion
Setting the two expressions for F equal gives us:
mtotal⋅a=(ρliquid⋅g⋅A−k)⋅x
This is a second-order differential equation that describes simple harmonic motion.
Step 6: Find the Period of Oscillation
The standard form of the equation for simple harmonic motion is:
mtotal⋅d2xdt2+keff⋅x=0
where keff=k−ρliquid⋅g⋅A.
The period T of small oscillations is given by:
T=2π√mtotalkeff
Substituting keff and mtotal:
T=2π√ρ⋅A⋅L+mk−ρliquid⋅g⋅A
Final Answer
Thus, the period of small oscillations is:
T=2π√ρ⋅A⋅L+mk−ρliquid⋅g⋅A
We have a rod of length L, cross-sectional area A, and density ρ hanging from a rigid support via a spring with stiffness k. A small sphere of mass m is attached at the bottom of the rod, and the rod is partially immersed in a liquid of density ρliquid.
When the rod is displaced downward by a small distance x, two forces will act on it:
1. Buoyant Force: The increase in buoyant force when the rod is displaced by x is given by:
Fbuoyant=ρliquid⋅g⋅Vdisplaced=ρliquid⋅g⋅(A⋅x)
where Vdisplaced=A⋅x is the volume of the rod that is now submerged.
Fspring=k⋅x
The net force F acting on the system when displaced by x is the sum of the buoyant force and the spring force:
F=Fbuoyant−Fspring=ρliquid⋅g⋅(A⋅x)−k⋅x
This can be simplified to:
F=(ρliquid⋅g⋅A−k)⋅x
According to Newton's second law, the net force is also equal to the mass times acceleration:
F=mtotal⋅a
where mtotal is the total mass of the system. The total mass includes the mass of the rod and the mass of the sphere:
mtotal=ρ⋅A⋅L+m
Setting the two expressions for F equal gives us:
mtotal⋅a=(ρliquid⋅g⋅A−k)⋅x
This is a second-order differential equation that describes simple harmonic motion.
The standard form of the equation for simple harmonic motion is:
mtotal⋅d2xdt2+keff⋅x=0
where keff=k−ρliquid⋅g⋅A.
T=2π√mtotalkeff
Substituting keff and mtotal:
T=2π√ρ⋅A⋅L+mk−ρliquid⋅g⋅A
Thus, the period of small oscillations is:
T=2π√ρ⋅A⋅L+mk−ρliquid⋅g⋅A
Similar Questions
A uniform heavy rod of weight W, cross sectional area a and length L is hanging from fixed support. Young modulus of the material of the rod is Y. Neglect the lateral contraction. Find the elongation of the rod.
View SolutionThere is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionA spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
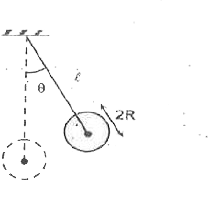 View Solution
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 View Solution
View SolutionTwo rods AB and BC of equal cross-sectional area A and Young's constant Y1 and Y2 are joined and suspended from a fixed support A. A block of mass M is attached to the lowest point C. The density of the rods is negligibly small. Find displacement of the point C.
 View Solution
View SolutionDerive an expression for the angular frequency of small oscillation of the bob of a simple pendulum when it is immerased in a liquid of density ρ. Assume the density of the bob as σ and length of the string as l.
View SolutionA non-conducting rod having circular cross section of radius R is suspended from a rigid support as shown in fig. A light and small coil of 300turns is wrapped tightly at the left end where uniform magnetic filed B exists in vertically downward direction. Air of density ρ hits the half of the right part of the rod with velocity V as shown in the fig. What should be current in clockwise direction (as seen from O) in the coil so that rod remains horizontal? Give answer in mA. Given 2Lv√πRBρ=1√5A−1/2.
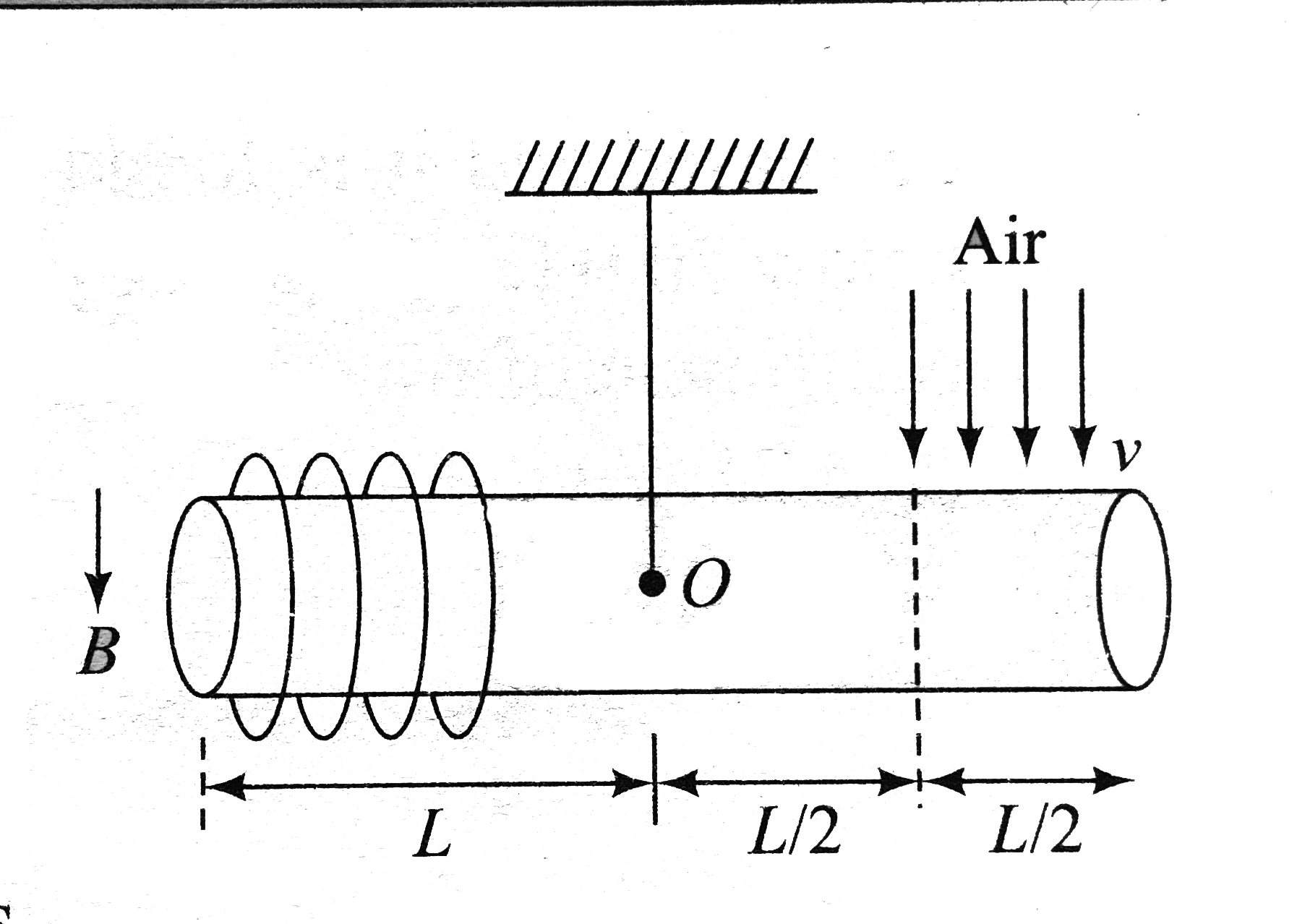 View Solution
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
 View Solution
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 View Solution
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 View Solution
View Solution
