A large open top container of negligible mass and uniform cross sectional area A a has a small hole of cross sectional area A/100 in its side wall near the bottom. The container is kept on a smooth horizontal floor and contains a liquid of density ρ and mass M0. Assuming that the liquid starts flowing out horizontally through the hole at t=0, calculate a the acceleration of the container and its velocity when 75% of the liquid has drained out.
To solve the problem, we will follow these steps:
Step 1: Determine the initial conditions
- The initial mass of the liquid in the container is M0.
- The cross-sectional area of the hole is A/100.
- The density of the liquid is ρ.
Step 2: Calculate the height of the liquid when 75% has drained out
When 75% of the liquid has drained out, 25% of the liquid remains. The remaining mass of the liquid is:
M=0.25M0
The volume of the liquid can be expressed as:
V=Mρ=0.25M0ρ
Since the volume of the liquid is also equal to the cross-sectional area of the container multiplied by the height h of the liquid:
V=A⋅h
Setting the two expressions for volume equal gives:
A⋅h=0.25M0ρ
From this, we can solve for h:
h=0.25M0Aρ
Step 3: Calculate the efflux speed of the liquid
Using Torricelli's theorem, the efflux speed v of the liquid flowing out of the hole is given by:
v=√2gh
Substituting h from Step 2:
v=√2g⋅0.25M0Aρ=√0.5gM0Aρ
Step 4: Calculate the acceleration of the container
The thrust force F acting on the container due to the outflow of liquid can be expressed as:
F=dmdt⋅v
The rate of change of mass dmdt can be calculated as:
dmdt=−ρ⋅A100⋅v
Substituting this into the thrust force equation gives:
F=−ρ⋅A100⋅v⋅v=−ρ⋅A100⋅(√0.5gM0Aρ)2
Simplifying this:
F=−ρ⋅A100⋅0.5gM0Aρ=−0.5gM0100
The acceleration a of the container can be found using Newton's second law F=ma:
a=FM=−0.5gM01000.25M0=−0.5g25=−g50
Step 5: Calculate the velocity of the container when 75% of the liquid has drained out
The velocity of the container Vc can be calculated using the relationship between acceleration and time. Assuming the acceleration is constant, the velocity can be expressed as:
Vc=a⋅t
However, we need to find the time t it takes for 75% of the liquid to drain out. The volume flow rate Q is given by:
Q=Ahole⋅v=A100⋅√0.5gM0Aρ
The total volume of liquid drained when 75% has drained is:
Vdrained=0.75⋅M0ρ
Setting Q⋅t=Vdrained gives us:
t=0.75⋅M0ρQ=0.75⋅M0ρA100⋅√0.5gM0Aρ
This will yield a value for t which can then be substituted back into the equation for Vc.
Final Answers
1. The acceleration of the container is:
a=−g50
2. The velocity of the container when 75% of the liquid has drained out can be calculated using the time found above.
- The initial mass of the liquid in the container is M0.
- The cross-sectional area of the hole is A/100.
- The density of the liquid is ρ.
When 75% of the liquid has drained out, 25% of the liquid remains. The remaining mass of the liquid is:
M=0.25M0
The volume of the liquid can be expressed as:
V=Mρ=0.25M0ρ
Since the volume of the liquid is also equal to the cross-sectional area of the container multiplied by the height h of the liquid:
V=A⋅h
Setting the two expressions for volume equal gives:
A⋅h=0.25M0ρ
From this, we can solve for h:
h=0.25M0Aρ
Using Torricelli's theorem, the efflux speed v of the liquid flowing out of the hole is given by:
v=√2gh
Substituting h from Step 2:
v=√2g⋅0.25M0Aρ=√0.5gM0Aρ
The thrust force F acting on the container due to the outflow of liquid can be expressed as:
F=dmdt⋅v
The rate of change of mass dmdt can be calculated as:
dmdt=−ρ⋅A100⋅v
Substituting this into the thrust force equation gives:
F=−ρ⋅A100⋅v⋅v=−ρ⋅A100⋅(√0.5gM0Aρ)2
Simplifying this:
F=−ρ⋅A100⋅0.5gM0Aρ=−0.5gM0100
The acceleration a of the container can be found using Newton's second law F=ma:
a=FM=−0.5gM01000.25M0=−0.5g25=−g50
The velocity of the container Vc can be calculated using the relationship between acceleration and time. Assuming the acceleration is constant, the velocity can be expressed as:
Vc=a⋅t
However, we need to find the time t it takes for 75% of the liquid to drain out. The volume flow rate Q is given by:
Q=Ahole⋅v=A100⋅√0.5gM0Aρ
The total volume of liquid drained when 75% has drained is:
Vdrained=0.75⋅M0ρ
Setting Q⋅t=Vdrained gives us:
t=0.75⋅M0ρQ=0.75⋅M0ρA100⋅√0.5gM0Aρ
This will yield a value for t which can then be substituted back into the equation for Vc.
1. The acceleration of the container is:
a=−g50
2. The velocity of the container when 75% of the liquid has drained out can be calculated using the time found above.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.2
11 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A large open top container of negligible mass and uniform cross sectional area A has a small uniform cross sectional area a in its side wall near the bottom. The container is kept over a smooth horizontal floor and contains a liquid of density ρ and mass m0. Assuming that the liqud starts flowing through the hole A the acceleration of the container will be
View SolutionA liquid is flowing through a pipe of non-uniform cross-section. At a point where area of cross-section of the pipe is less, match the following columns.

View SolutionA fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
View SolutionA body of uniform cross-sectional area floats in a liquid of density thrice its value. The portion of exposed height will be :
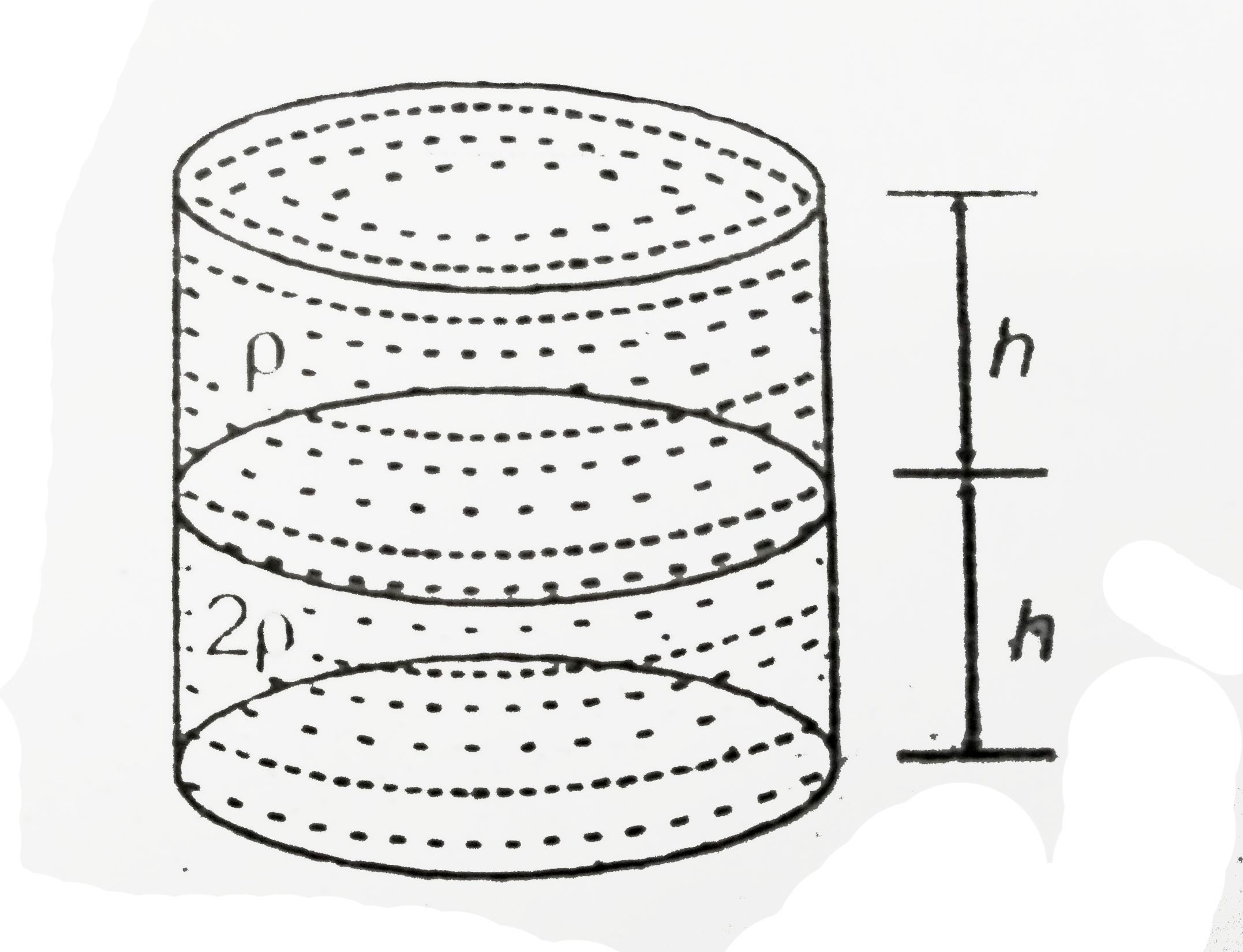
View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
View SolutionThe velocity of the liquid coming out of a small hole of a vessel containing two different liquids of densities 2ρ and ρ as shown in the figure is

View SolutionThe velocity of the liquid coming out of a small hole of a vessel containing two different liquids of densities 2ρ and ρ as shown in the figure is

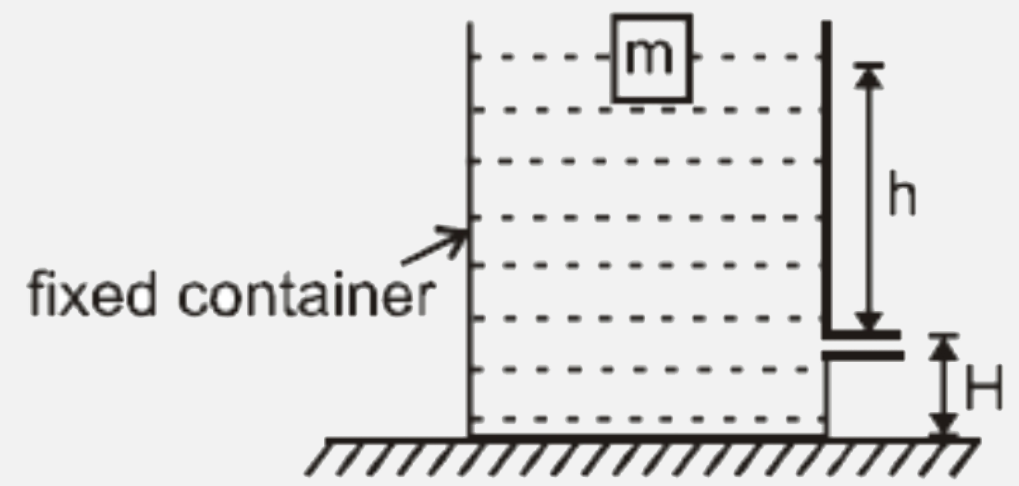
View SolutionIf the pin hole in the container is very small compared to the area of the base of container and a block floats in the ideal liquid then, the speed of efflux is
View SolutionA container shown in Fig. is accelerated horizontally with acceleration a.
a. Find the minimum value of a at which liquid just starts spilling out.

View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View Solution
