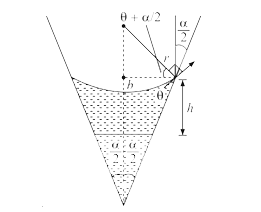
A glass capillary tube is of the shape of a truncated cone with an apex angle $α$ so that its two ends have cross sections of different radii. When dipped in water vertically, water rises in it to a high h, where the radius of its cross section is b. If the surface tension of water is S, its density if $ρ$ , and its contact angle with glass is $θ$ , the value of h will be (g is the acceleration due to gravity)

$\frac{2 S}{b ρ g} cos (θ - α)$

$\frac{2 S}{b ρ g} cos (θ + α)$

$\frac{2 S}{b ρ g} cos (θ - α / 2)$

$\frac{2 S}{b ρ g} cos (θ + α / 2)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

When two capillary tubes of different diameters are dipped vertically, the rise of the liquids is
Asame in both the tubes
Bmore in tube of larger diameter
Cless in tube of smaller diameter
Dmore in the tube of smaller diameter