Consider a thin square plate floating on a viscous liquid in a large tank. The height h of the liquid in the tank is much less than the width of the tank. The floating plate is pulled horizontally with a constant velocity u0. Which of the following statement is (are) true ?
The resistive force of liquid on the plate is inversely proportional to h
The resistive force of liquid on the plate is independent of the area of the plate
The tangential (shear) stress on the floor of the tank increases with u0
the tangential (shear) stress on the plate varies linearly with the viscosity η of the liquid
The correct Answer is:A, C, D
To solve the problem, we need to analyze the situation of a thin square plate floating on a viscous liquid and being pulled horizontally with a constant velocity u0. We will evaluate the statements provided in the question based on the principles of fluid mechanics, particularly Newton's law of viscosity.
1. Understanding the Setup:
- We have a tank filled with a viscous liquid, and the height h of the liquid is much smaller than the width of the tank.
- A thin square plate is floating on the surface of this liquid and is being pulled horizontally with a constant velocity u0.
2. Applying Newton's Law of Viscosity:
- According to Newton's law of viscosity, the viscous force F acting on the plate can be expressed as:
F=ηAdudy
- Where η is the dynamic viscosity of the liquid, A is the area of the plate, and dudy is the velocity gradient perpendicular to the direction of flow.
3. Determining the Velocity Gradient:
- The velocity profile across the height of the liquid can be assumed linear due to the viscous drag. At the surface of the liquid (where the plate is), the velocity is u0, and at the bottom of the liquid (at height h), the velocity is 0.
- Thus, the velocity gradient dudy can be calculated as:
dudy=u0−0h=u0h
4. Calculating the Viscous Force:
- Substituting the velocity gradient back into the equation for viscous force:
F=ηAu0h
- This shows that the viscous force is directly proportional to the area A of the plate and inversely proportional to the height h.
5. Evaluating the Statements:
- Statement A: The resistive force of the liquid is inversely proportional to h.
- True: We derived that F∝1h.
- Statement B: The resistive force on the plate is independent of the area.
- False: The resistive force is directly proportional to the area A.
- Statement C: The shear stress on the floor of the tank will increase with u0.
- True: As u0 increases, the viscous force increases, leading to higher shear stress.
- Statement D: The tangential shear on the plate varies linearly with viscosity.
- True: The viscous force is directly proportional to the viscosity η.
6. Conclusion:
- The correct statements are A, C, and D.
Summary of Correct Statements:
- A: True
- B: False
- C: True
- D: True
- We have a tank filled with a viscous liquid, and the height h of the liquid is much smaller than the width of the tank.
- A thin square plate is floating on the surface of this liquid and is being pulled horizontally with a constant velocity u0.
- According to Newton's law of viscosity, the viscous force F acting on the plate can be expressed as:
F=ηAdudy
- Where η is the dynamic viscosity of the liquid, A is the area of the plate, and dudy is the velocity gradient perpendicular to the direction of flow.
- The velocity profile across the height of the liquid can be assumed linear due to the viscous drag. At the surface of the liquid (where the plate is), the velocity is u0, and at the bottom of the liquid (at height h), the velocity is 0.
- Thus, the velocity gradient dudy can be calculated as:
dudy=u0−0h=u0h
- Substituting the velocity gradient back into the equation for viscous force:
F=ηAu0h
- This shows that the viscous force is directly proportional to the area A of the plate and inversely proportional to the height h.
- Statement A: The resistive force of the liquid is inversely proportional to h.
- True: We derived that F∝1h.
- Statement B: The resistive force on the plate is independent of the area.
- False: The resistive force is directly proportional to the area A.
- Statement C: The shear stress on the floor of the tank will increase with u0.
- True: As u0 increases, the viscous force increases, leading to higher shear stress.
- Statement D: The tangential shear on the plate varies linearly with viscosity.
- True: The viscous force is directly proportional to the viscosity η.
- The correct statements are A, C, and D.
- A: True
- B: False
- C: True
- D: True
Topper's Solved these Questions
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE MAIN (LEVEL - 1 )
Explore 31 Videos
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:IMPECCABLE
Explore 53 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Advanced (Archive)
Explore 78 Videos
Similar Questions
A flat plate is moving normal to its plane through a gas under the action of a constant force F. The gas is kept at a very low pressure. The speed of the plate v is much less than the average speed u of the gas molecules. Which of the following options is/are true ?
View SolutionA broad metal plane is connected to earth through a conducting wire as shown. An electron flies with constant velocity along a straight line above the plate at a distance much less than the linear dimensions of the plate. If the current I flowing from the earth to the plate is considered to be positive, then which of the following graph correctly depicts the variation of current I with time ?
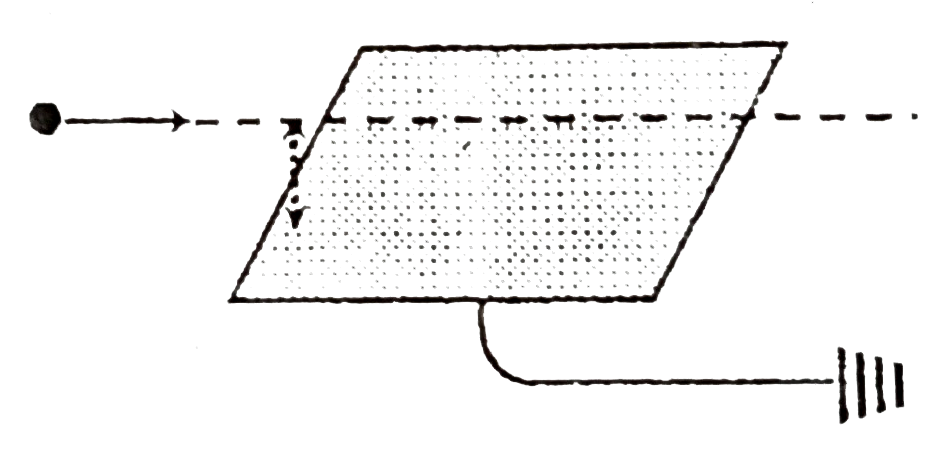
View Solution
Knowledge Check
The rotation rate of a mixing blade, in rotations per second, slows as a liquid is being added to the mixer. The blade rotates at 1,000 rotations per second when the mixer is empty. The rate at which the blade slows is four rotations per second less than three times the square of the height of the liquid. If h is the height of liquid in the mixer, which of the following represents R(h), the rate of rotation?
A4−9h2B1,000−(4−3h)C1,000−(9h−4)D1,000−(3h2−4)
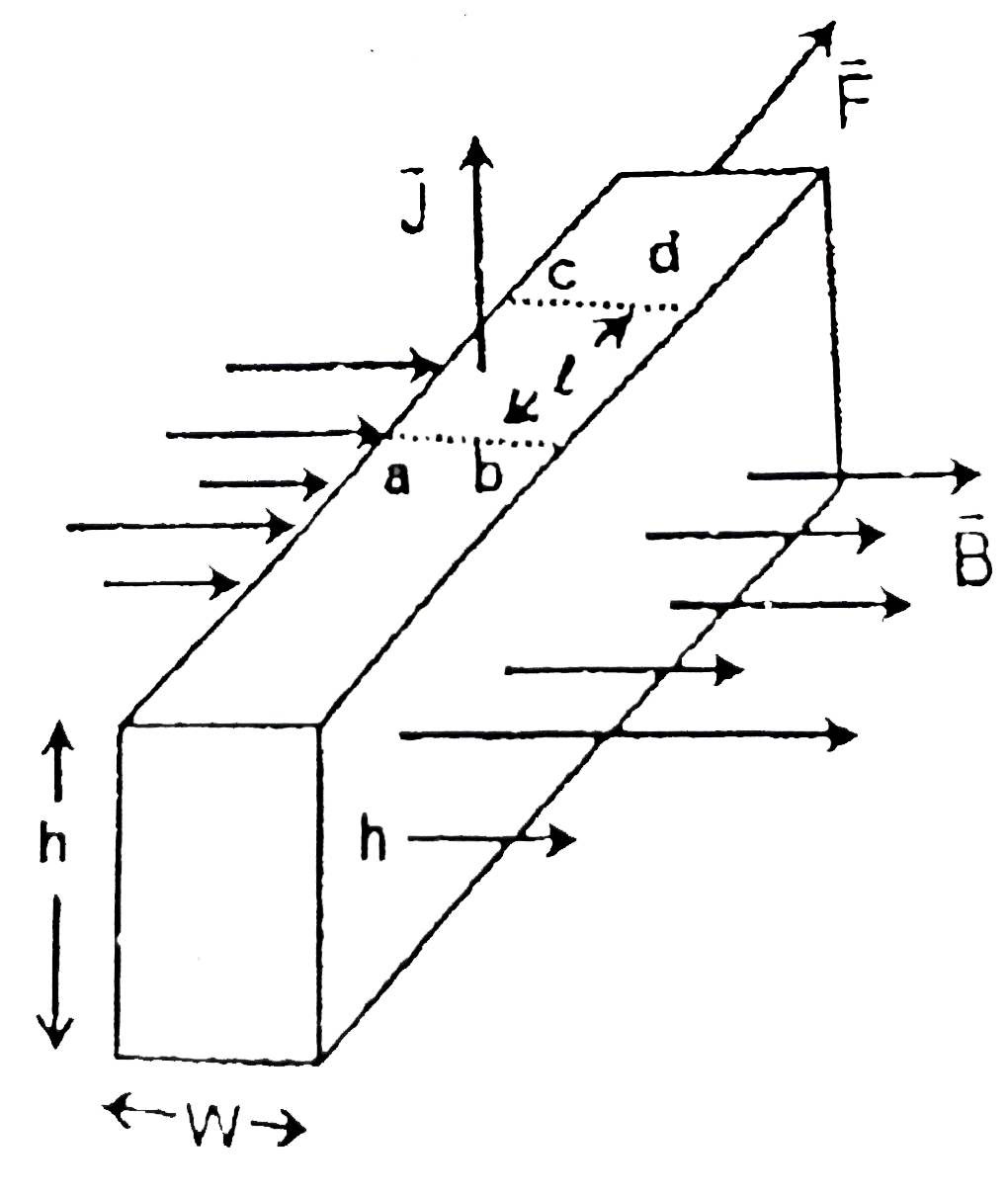
Magnetic forces acting on conducting fluids provide a convenient means of pumping these fluids. For example, this method can be used to pump blood without damage to the cells that can be caused by a mechanical pump. A horizontal tube with rectangular cross section (height h, width W) is placed at right angles to a uniform magnetic field with magnitude B so that a length l is in the field (see figure). The tube is filled with conducting liquid and an electric current density J is maintained in the third mutually perpendicular direction.
Which of the following statement is true ?
View SolutionA thin plate AB of large area A is placed symmetrically in a small gap of height h filled with water of viscosity η0and the plate has a constant velocity v by applying a force F as shown in the figure. If the gap is filled with some other liquid of viscosity 0.75η0 at what minimum distance (in cm) from top wall should the plate be placed in the gap, so that the plate can again be pulled at the same constant velocity V. by applying the same force F? (Take h=20cm)
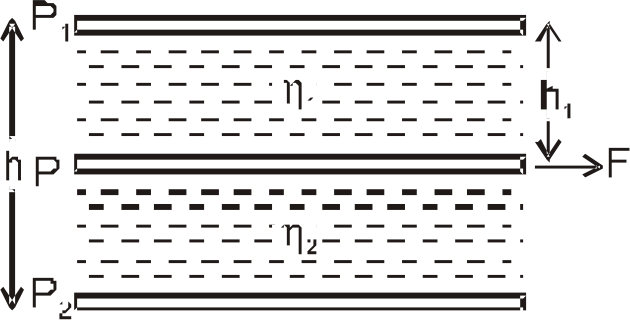
View SolutionA thin horizontal movable plate P is separated from two fixed horizontal plates P1 and P2 by two highly viscous liquids of coefficient of viscosity η1 and η2 as shown, where η2=4η1. Area of contact of movable plate with each fluid is same. If the distance between two fixed plates is h, then the distance h1 of movable plate from upper fixed plate such that the movable plate can be moved with a constant velocity by applying a minimum constant horizontal force F on movable plate is (assume velocity gradient to be uniform in each liquid).
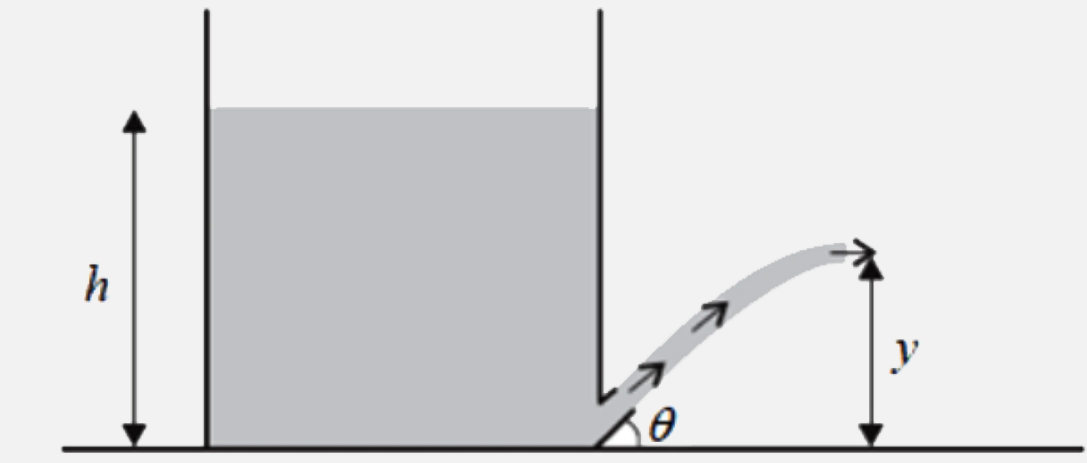
View SolutionA stream of non-viscous liquid emerges from a very short outlet tube at the base of a large . Open tank , in which the depth of liquid is h. The tube is at a fixed angle θ to the ground as shown in the figure. The maximum height of the stream y is
View SolutionA very large, charged plate floats in deep space. Due to the charge on the plate, a constant electric field E exists everry above the plate. An object with mass m and charge -q is shot upward from the plate with a velocity v and at an angle θ. It follows the path shown reaching a height h and a ramge R. Assume the effects of gravity to be negligible.

Which of the following is true concerning all objects the path shown when propelled with a velocity v at an angle θ?
View SolutionA very large, charged plate floats in deep space. Due to the charge on the plate, a constant electric field E exists everry above the plate. An object with mass m and charge -q is shot upward from the plate with a velocity v and at an angle θ. It follows the path shown reaching a height h and a ramge R. Assume the effects of gravity to be negligible.
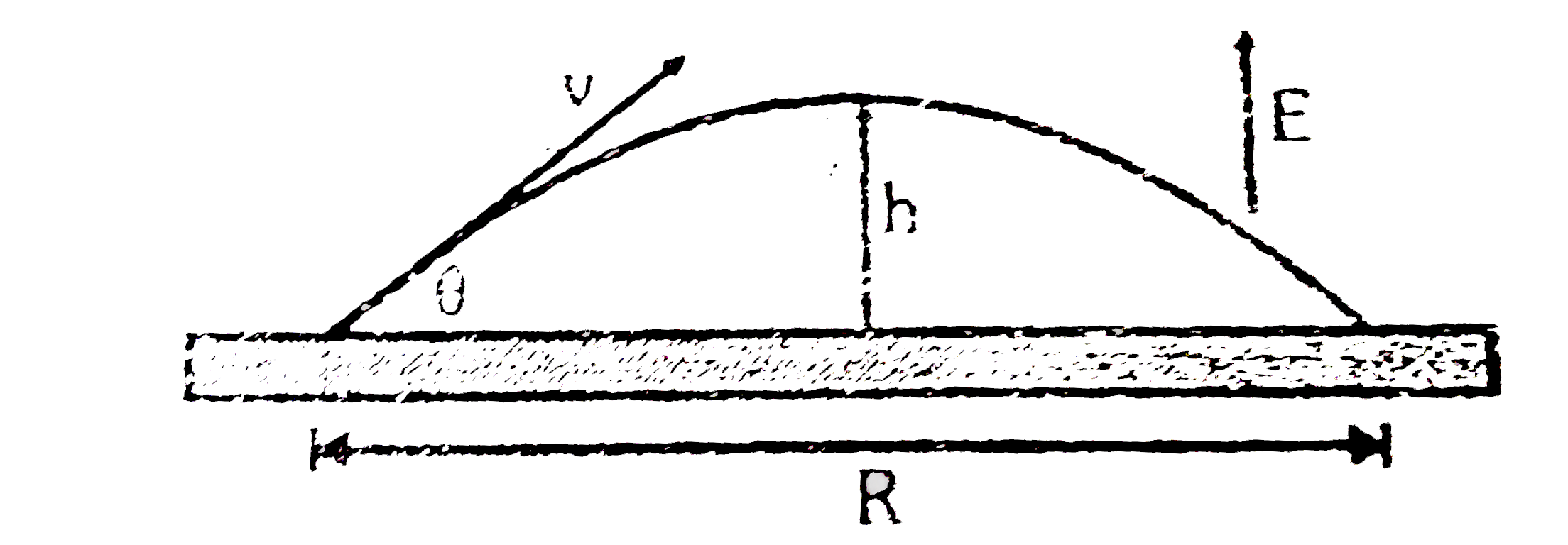
Which of the following is true concerning the flight of the projectile shown?
View SolutionA very large, charged plate floats in deep space. Due to the charge on the plate, a constant electric field E exists everry above the plate. An object with mass m and charge q is shot upward from the plate with a velocity v and at an angle θ. It follows the path shown reaching a height h and a ramge R. Assume the effects of gravity to be negligible.
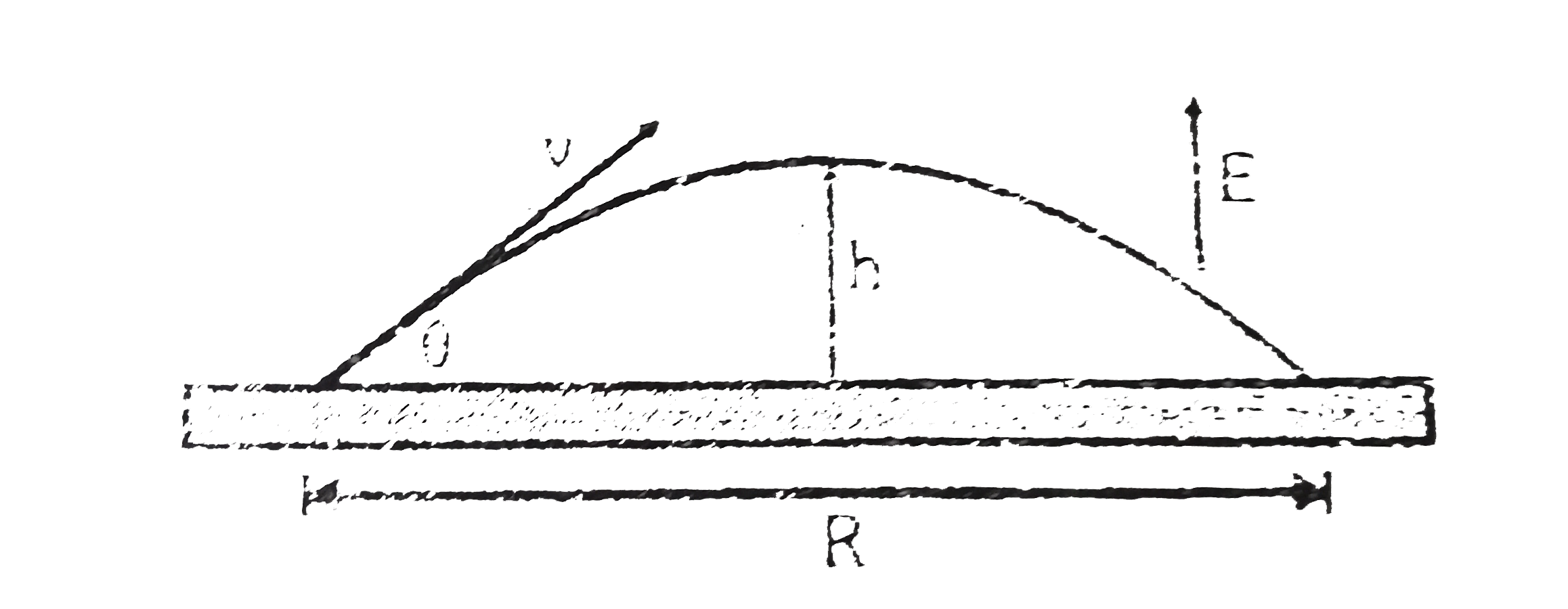
Which of the following must be true concentration the object?
View Solution