A thin plate AB of large area A is placed symmetrically in a small gap of height h filled with water of viscosity η0and the plate has a constant velocity v by applying a force F as shown in the figure. If the gap is filled with some other liquid of viscosity 0.75η0 at what minimum distance (in cm) from top wall should the plate be placed in the gap, so that the plate can again be pulled at the same constant velocity V. by applying the same force F? (Take h=20cm)
The correct Answer is:5
To solve the problem, we need to analyze the viscous forces acting on the plate in two different scenarios: when the gap is filled with water and when it is filled with a liquid of viscosity 0.75η0.
1. Understanding the Setup:
- We have a thin plate AB placed symmetrically in a gap of height h=20cm.
- The plate moves with a constant velocity v when a force F is applied.
- The viscosity of the first liquid (water) is η0.
2. Case 1: Viscosity η0:
- When the gap is filled with water, the viscous force F acting on the plate can be expressed as:
F=η0⋅v⋅Ah
- Here, A is the area of the plate, and h is the height of the gap.
3. Case 2: Viscosity 0.75η0:
- Now, we need to find the minimum distance y from the top wall where the plate can be placed to maintain the same velocity v under the same force F.
- The new viscosity is 0.75η0, and the effective height of the gap is now y and h−y.
4. Force Calculation for Case 2:
- The viscous force in this case can be expressed as:
F=0.75η0⋅v⋅Ay+0.75η0⋅v⋅Ah−y
- This can be simplified to:
F=0.75η0vA(1y+1h−y)
5. Equating Forces:
- Since the force F remains the same in both cases, we can set the equations equal to each other:
η0⋅v⋅Ah=0.75η0vA(1y+1h−y)
- Dividing both sides by η0vA (assuming they are non-zero):
1h=0.75(1y+1h−y)
6. Solving the Equation:
- Rearranging gives:
1h=0.75y+0.75h−y
- Multiplying through by y(h−y):
y(h−y)h=0.75(h−y)+0.75y
- Simplifying leads to:
y(h−y)h=0.75h
- Cross-multiplying gives:
y(h−y)=0.75h2
7. Substituting h=20cm:
- Substitute h=20cm:
y(20−y)=0.75⋅202
y(20−y)=0.75⋅400
y(20−y)=300
8. Solving the Quadratic Equation:
- Rearranging gives:
y2−20y+300=0
- Using the quadratic formula y=−b±√b2−4ac2a:
y=20±√(−20)2−4⋅1⋅3002⋅1
y=20±√400−12002
y=20±√−8002
- Since we need a real solution, we can find two possible values for y which yield:
- y=5cm (minimum distance from the top)
- y=15cm (other possible distance)
9. Conclusion:
- The minimum distance from the top wall where the plate should be placed is:
5cm
- We have a thin plate AB placed symmetrically in a gap of height h=20cm.
- The plate moves with a constant velocity v when a force F is applied.
- The viscosity of the first liquid (water) is η0.
- When the gap is filled with water, the viscous force F acting on the plate can be expressed as:
F=η0⋅v⋅Ah
- Here, A is the area of the plate, and h is the height of the gap.
- Now, we need to find the minimum distance y from the top wall where the plate can be placed to maintain the same velocity v under the same force F.
- The new viscosity is 0.75η0, and the effective height of the gap is now y and h−y.
- The viscous force in this case can be expressed as:
F=0.75η0⋅v⋅Ay+0.75η0⋅v⋅Ah−y
- This can be simplified to:
F=0.75η0vA(1y+1h−y)
- Since the force F remains the same in both cases, we can set the equations equal to each other:
η0⋅v⋅Ah=0.75η0vA(1y+1h−y)
- Dividing both sides by η0vA (assuming they are non-zero):
1h=0.75(1y+1h−y)
- Rearranging gives:
1h=0.75y+0.75h−y
- Multiplying through by y(h−y):
y(h−y)h=0.75(h−y)+0.75y
- Simplifying leads to:
y(h−y)h=0.75h
- Cross-multiplying gives:
y(h−y)=0.75h2
- Substitute h=20cm:
y(20−y)=0.75⋅202
y(20−y)=0.75⋅400
y(20−y)=300
- Rearranging gives:
y2−20y+300=0
- Using the quadratic formula y=−b±√b2−4ac2a:
y=20±√(−20)2−4⋅1⋅3002⋅1
y=20±√400−12002
y=20±√−8002
- Since we need a real solution, we can find two possible values for y which yield:
- y=5cm (minimum distance from the top)
- y=15cm (other possible distance)
- The minimum distance from the top wall where the plate should be placed is:
5cm
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Fill In The Blanks
1 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - SCQ_TYPE
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Linked Comprehension
30 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A thin plate of large area is placed midway in a gap of height h filled with oil of viscosity and the plate is pulled at constant velocity vby applying the same drag force on the plate. If a lighter oil of viscosity η is then substituted in the gap. it is found that for the velocity v, and the same drag force as previous case the plate is located unsymmetrically in the gap but parallel to the walls. Find η in terms of distance from nearer wall to the plane y.
View SolutionWhat is SI unit of viscosity coefficient (η) ?
View Solution
Knowledge Check
What is SI unit of viscosity coefficient (η) ?
ApascalBNsm−2Ckm−2sDNm−2A copper plate of thickness b is placed inside a parallel plate capacitor of plate distance d and area A as shown in figure. The capacitance of capacitor is
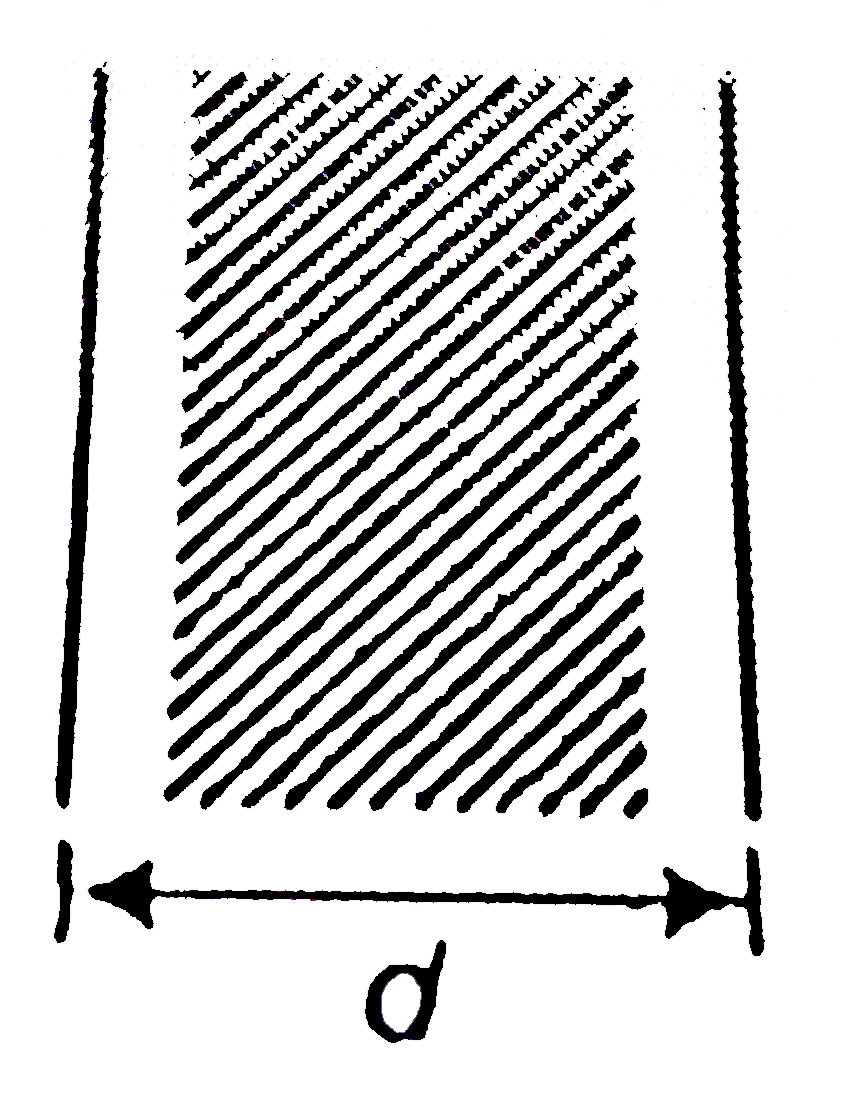 Aε0Ad+b2Bε0A2dCε0Ad−bD2ε0Ad+b2
Aε0Ad+b2Bε0A2dCε0Ad−bD2ε0Ad+b2
A square plate of 0.1 m side moves parallel to another plate with a velocity of 0.1ms−1 both plates immersed in water. If the viscous force is 0.02 N and the coefficient of viscosity 0.01 poise, what is the distance apart?
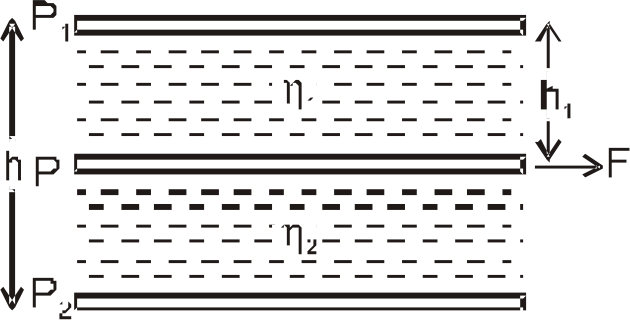
View SolutionA thin horizontal movable plate P is separated from two fixed horizontal plates P1 and P2 by two highly viscous liquids of coefficient of viscosity η1 and η2 as shown, where η2=4η1. Area of contact of movable plate with each fluid is same. If the distance between two fixed plates is h, then the distance h1 of movable plate from upper fixed plate such that the movable plate can be moved with a constant velocity by applying a minimum constant horizontal force F on movable plate is (assume velocity gradient to be uniform in each liquid).
View SolutionA very thin plate of metal is placed exactly in the middle of the two plates of a parallel plate capacitor. What will be the effect on the capacitance of the system?
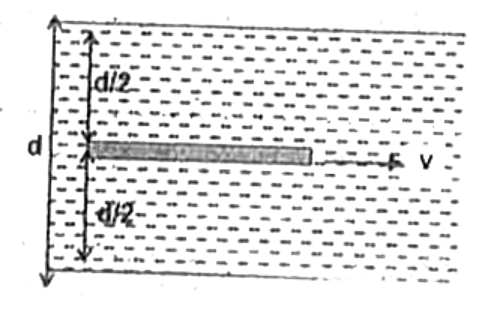
View SolutionA thin square plate of side φ=10cm is dragged with constant velocity v=3 cm/s in an oil . The width 'd' of the oil column is 2mm. Square plate is placed symmetrically as shown in the figure. Assumed velocity of layer of oil at the end is negligible. The coefficient of viscosity is 150 poise. Find the horizontal force (in Newton) required to move the square plate with constant velocity
View SolutionFour identical metal plates are placed in air parallel to each other with distances d from one another. The area of each plate is equal to A. The arrangement is shown in the figure. Find the capacitance of the system between plates P and R.

View SolutionA man is rowing a boat with a constant velocity v0 in a river. The contact area of boat is 'A' and coefficient of viscosity is η. The depth of river is 'D' . Find the force required to row the boat.
View Solution
