A solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
(a)The net elongation of the spring is 4πR3ρg3k
(b)The net elongation of the spring is 8πR3ρg3k
(c)The light sphere is partially submerged
(d)the light sphere is completely submerged
The correct Answer is:A, D
To solve the problem, we need to analyze the forces acting on the two spheres and the spring connecting them when the system reaches equilibrium.
1. Identify the parameters:
- Sphere 1: Radius = R, Density = ρ
- Sphere 2: Radius = R, Density = 3ρ
- Liquid Density = 2ρ
- Spring constant = k
2. Calculate the volume of each sphere:
The volume V of a sphere is given by the formula:
V=43πR3
3. Calculate the buoyant force acting on each sphere:
The buoyant force Fb acting on a submerged object is given by:
Fb=Volume×Density of liquid×g
For Sphere 1 (density ρ):
Fb1=43πR3(2ρ)g=83πR3ρg
For Sphere 2 (density 3ρ):
Fb2=43πR3(2ρ)g=83πR3ρg
4. Calculate the weight of each sphere:
The weight W of an object is given by:
W=Volume×Density×g
For Sphere 1:
W1=43πR3ρg
For Sphere 2:
W2=43πR3(3ρ)g=4πR3ρg
5. Set up the equilibrium condition:
At equilibrium, the total buoyant force must equal the total weight of the spheres plus the force exerted by the spring:
Fb1+Fb2=W1+W2+Fs
Where Fs is the force exerted by the spring.
6. Calculate the net force:
The net buoyant force:
Fb=Fb1+Fb2=83πR3ρg+83πR3ρg=163πR3ρg
The total weight:
Wtotal=W1+W2=43πR3ρg+4πR3ρg=163πR3ρg
7. Force exerted by the spring:
Since the system is in equilibrium, we can equate the total buoyant force to the total weight:
Fb=Wtotal+Fs
Since Fb and Wtotal are equal, the spring force Fs must be zero at equilibrium.
8. Calculate the elongation of the spring:
The elongation x of the spring can be calculated using Hooke's law:
Fs=kx
Since the spring force is zero at equilibrium, the elongation is given by:
x=Fb−Wtotalk
Substituting the values:
x=163πR3ρg−163πR3ρgk=0
9. Conclusion:
The net elongation of the spring is zero, and both spheres are completely submerged.
Correct Statements:
- The net elongation of the spring is 4πR3ρg3k (if we consider the forces acting on the spring).
- Both spheres are completely submerged.
- Sphere 1: Radius = R, Density = ρ
- Sphere 2: Radius = R, Density = 3ρ
- Liquid Density = 2ρ
- Spring constant = k
The volume V of a sphere is given by the formula:
V=43πR3
The buoyant force Fb acting on a submerged object is given by:
Fb=Volume×Density of liquid×g
For Sphere 1 (density ρ):
Fb1=43πR3(2ρ)g=83πR3ρg
For Sphere 2 (density 3ρ):
Fb2=43πR3(2ρ)g=83πR3ρg
The weight W of an object is given by:
W=Volume×Density×g
For Sphere 1:
W1=43πR3ρg
For Sphere 2:
W2=43πR3(3ρ)g=4πR3ρg
At equilibrium, the total buoyant force must equal the total weight of the spheres plus the force exerted by the spring:
Fb1+Fb2=W1+W2+Fs
Where Fs is the force exerted by the spring.
The net buoyant force:
Fb=Fb1+Fb2=83πR3ρg+83πR3ρg=163πR3ρg
The total weight:
Wtotal=W1+W2=43πR3ρg+4πR3ρg=163πR3ρg
Since the system is in equilibrium, we can equate the total buoyant force to the total weight:
Fb=Wtotal+Fs
Since Fb and Wtotal are equal, the spring force Fs must be zero at equilibrium.
The elongation x of the spring can be calculated using Hooke's law:
Fs=kx
Since the spring force is zero at equilibrium, the elongation is given by:
x=Fb−Wtotalk
Substituting the values:
x=163πR3ρg−163πR3ρgk=0
The net elongation of the spring is zero, and both spheres are completely submerged.
- The net elongation of the spring is 4πR3ρg3k (if we consider the forces acting on the spring).
- Both spheres are completely submerged.
Topper's Solved these Questions
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )
31 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
Similar Questions
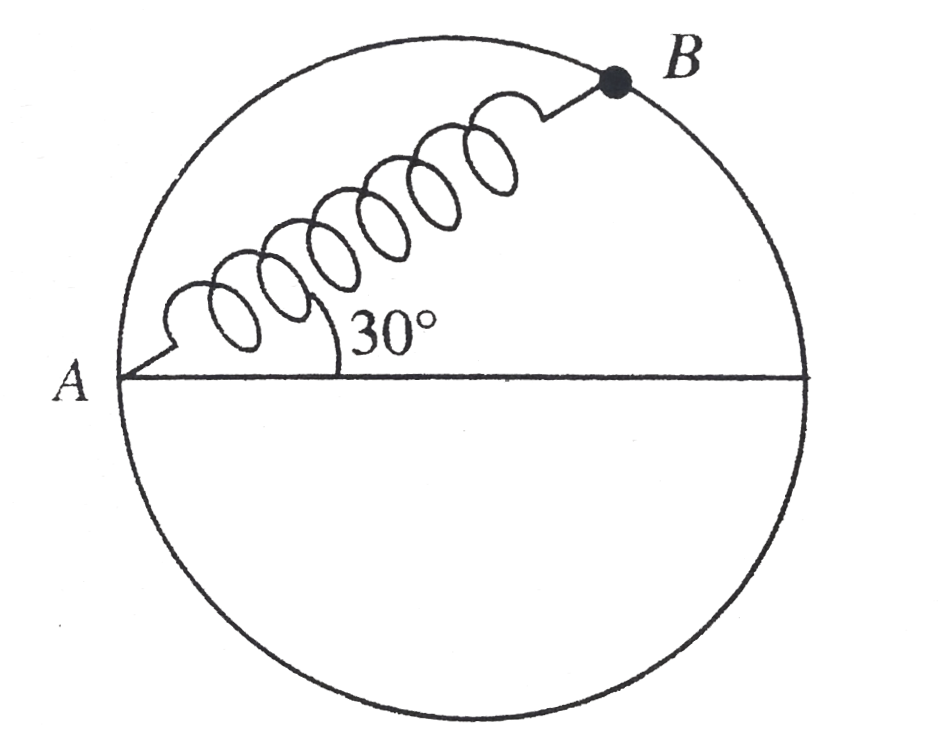
A bead of mass m is attached to one end of a spring of natural length R and spring constant K=(√3+1)mgR. The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is
View SolutionWhat is the moment of inertia of a solid sphere of density ρ and radius R about its diameter ?
View SolutionA block of density 2000kg/m3 and mass 10kg is suspended by a spring stiffness 100N/m. The other end of the spring is attached to a fixed support. The block is completely submerged in a liquid of density 1000kg/m3. If the block is in equilibrium position.
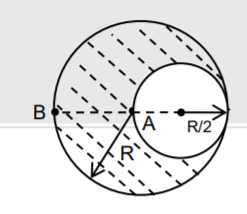
View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
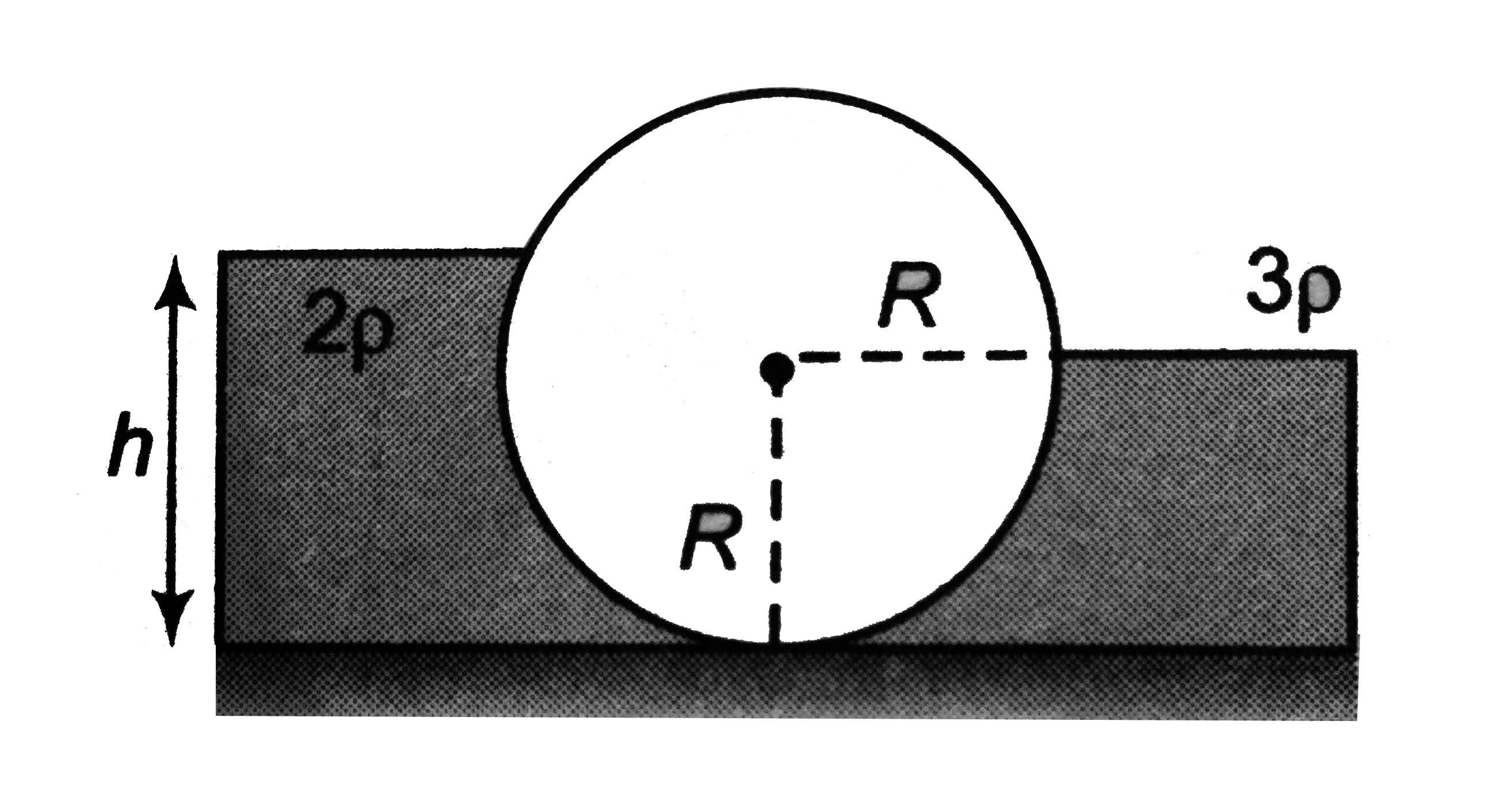
View SolutionIn the figure shown, the heavy cylinder (radius R) reasting on a smooth surface separates two liquids of densities 2ρ and 3ρ. The height h for the equilibrium of cylinder must be
View SolutionA Solid sphere of density ρ=ρ0(1−r2R2),0<r≤R just floats in a liquid then density of liquid is– (r is distance from centre of sphere)
View SolutionWhat is the moment of inertia of solid sphere of density ρ and radius R about its diameter ?
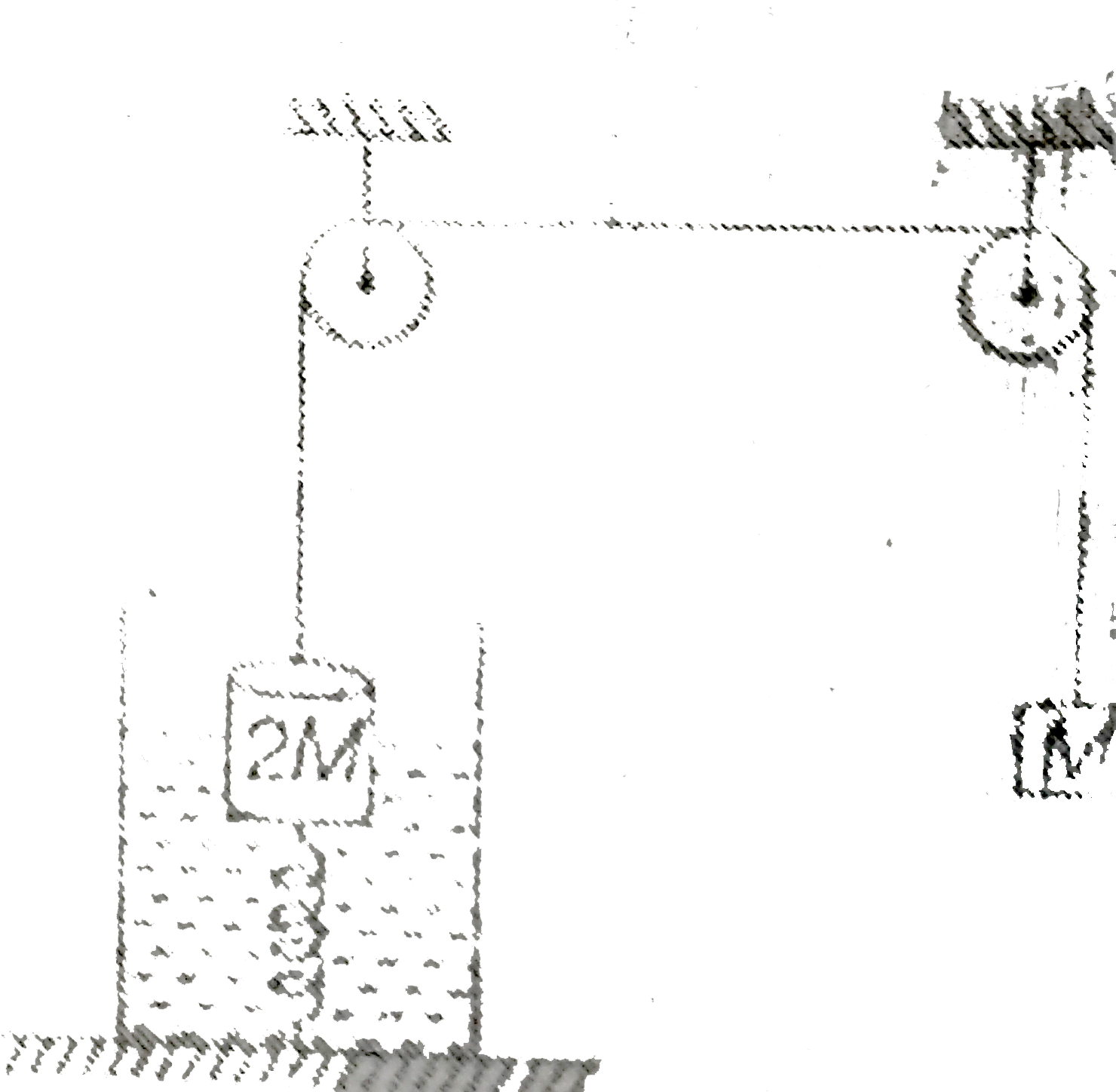
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
Under equilibrium conditions
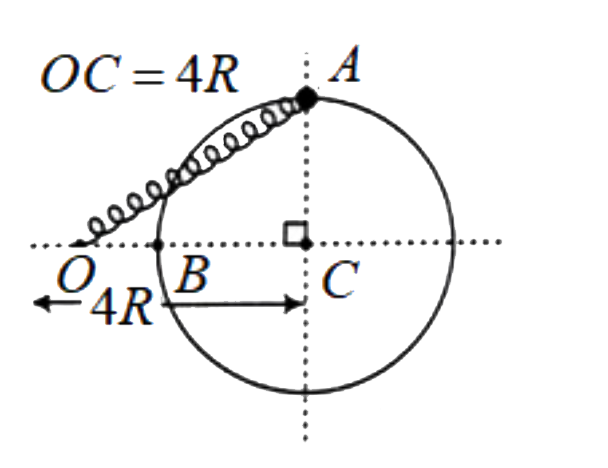
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
View SolutionConsider a solid sphere oF radius R and mass density ρ(r)=ρ0(1−r2R2) 0<r≤R. The minimum density oF a liquid in which it will Float is:
View Solution
