Consider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
The correct Answer is:90
To solve the problem of finding the angle x between the directions of motion of two balls after an oblique elastic collision, we can follow these steps:
Step 1: Understand the Collision
In an elastic collision between two balls of the same mass, the velocities of the balls change according to the conservation of momentum and kinetic energy. Since one ball is stationary and the other is moving, we can denote the moving ball's initial velocity as V and the stationary ball's initial velocity as 0.
Step 2: Analyze the Components of Velocity
During the collision, the component of the velocity along the line of impact will be exchanged between the two balls. If we denote the angle of incidence as θ, the component of the moving ball's velocity along the line of impact is Vcosθ, and the perpendicular component is Vsinθ.
Step 3: Apply Conservation of Momentum
After the collision, both balls move with the same speed V′. The ball that was initially moving transfers its velocity along the line of impact to the stationary ball. Therefore, the stationary ball will acquire a velocity Vcosθ, while the first ball will retain its perpendicular component Vsinθ.
Step 4: Determine the Angle Between the Velocities
After the collision, the two balls move at an angle x to each other. The first ball moves at an angle θ from the original direction, and the second ball moves in the direction of the line of impact. Since the two components of velocity are perpendicular to each other, we can conclude that the angle x between the two balls' velocities is 90∘.
Final Answer
Thus, the angle x between the directions of motion of the two balls after the collision is:
x=90∘
In an elastic collision between two balls of the same mass, the velocities of the balls change according to the conservation of momentum and kinetic energy. Since one ball is stationary and the other is moving, we can denote the moving ball's initial velocity as V and the stationary ball's initial velocity as 0.
During the collision, the component of the velocity along the line of impact will be exchanged between the two balls. If we denote the angle of incidence as θ, the component of the moving ball's velocity along the line of impact is Vcosθ, and the perpendicular component is Vsinθ.
After the collision, both balls move with the same speed V′. The ball that was initially moving transfers its velocity along the line of impact to the stationary ball. Therefore, the stationary ball will acquire a velocity Vcosθ, while the first ball will retain its perpendicular component Vsinθ.
After the collision, the two balls move at an angle x to each other. The first ball moves at an angle θ from the original direction, and the second ball moves in the direction of the line of impact. Since the two components of velocity are perpendicular to each other, we can conclude that the angle x between the two balls' velocities is 90∘.
Thus, the angle x between the directions of motion of the two balls after the collision is:
x=90∘
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:Level - 1 PARAGRAPH QUESTIONS
Explore 3 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2
Explore 48 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 0 - LONG ANSWER TYPE
Explore 5 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
A particle A suffers an oblique elastic collision particle B that is at rest initially. If their masses with a are the same, then after the collision
View SolutionA ball moving along a straight line collides elastically with another stationary ball of the same mass. At the moment of collision, the angle between the straight line passing through the centres of the balls and the direction of tr initial motion of the striking ball is θ, find the fraction of the kinetic energy of the striking ball converted into potential energy at the moment of the maximum deformation.
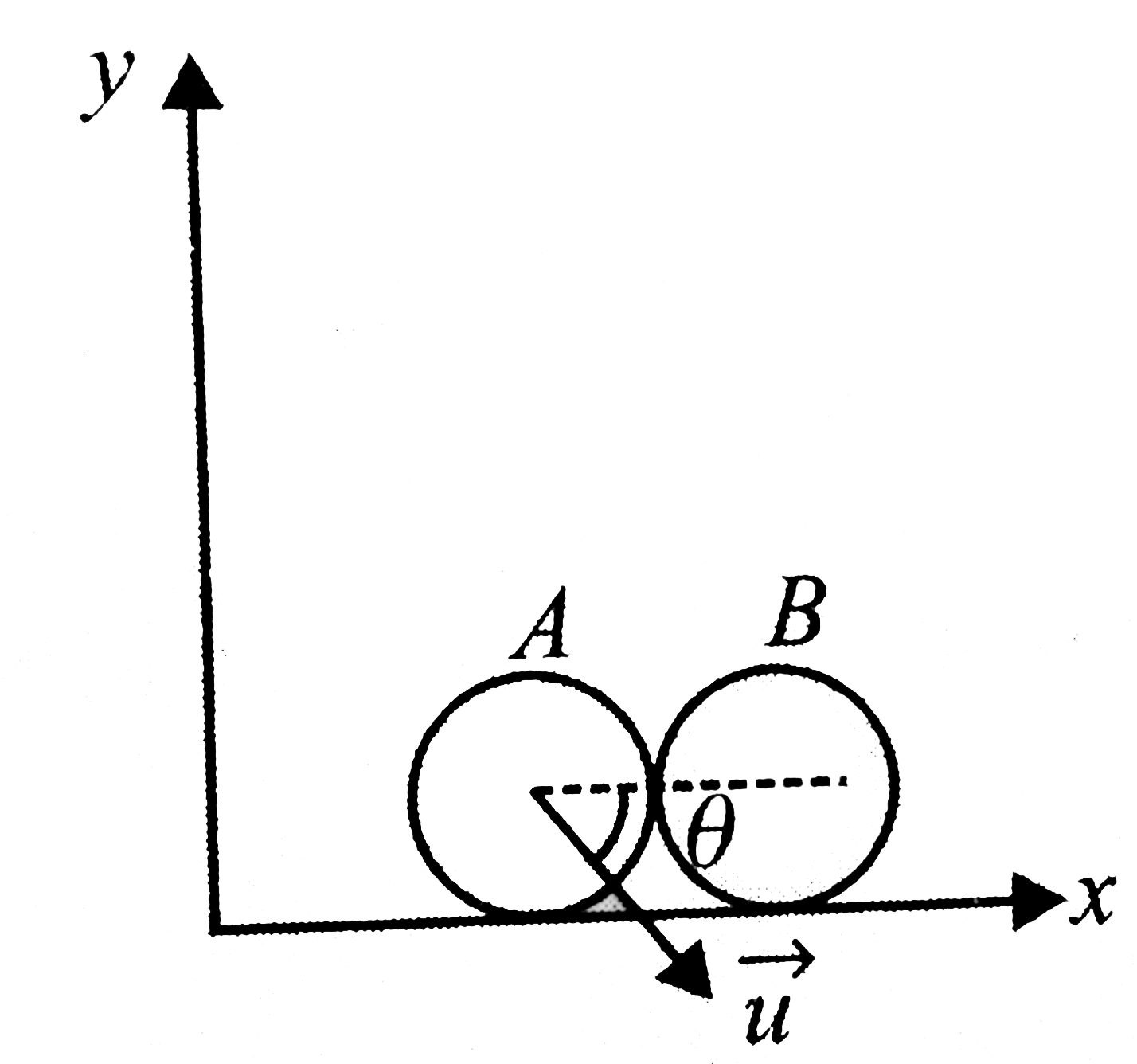
View SolutionTwo balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
View SolutionAn iron ball A collides with another stationary iron ball B If the ratio of radii of the balls is n = 2, find the ratio of their speeds just after the collision (e = 0.5)

View SolutionTwo identical billiard balls undergo an oblique elastic collision. Initially, one of the balls is stationary. If the initially stationary ball after collision moves in a direction which makes an angle of 37∘ with direction of initial motion of the moving ball, then the angle through which initially moving ball will be deflected is
View SolutionAfter perfectly inelastic collision between two identical balls moving with same speed in different directions, the speed of the combined mass becomes half the initial speed. Find the angle between the two before collision.
View SolutionTwo balls each of mass 2kg (one at rest) undergo oblique collision is perfectly elastic, then the angle between their velocities after collision is
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
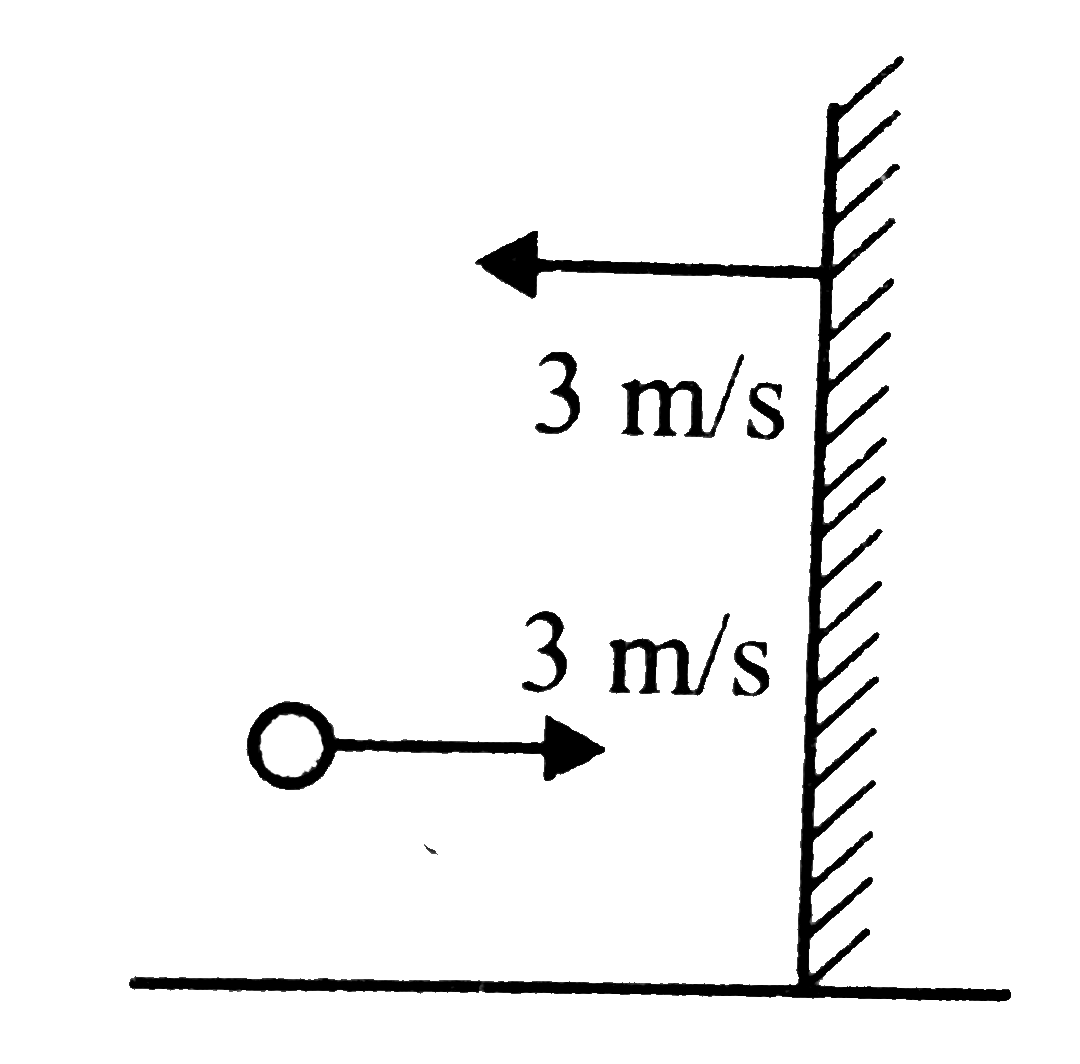
View SolutionBall A of mass m strickes a stationary ball B of mass M and undergoes an elastic collision. After collision bill A has a speed one third of its initial speed. The ratio of M/m is
View SolutionA ball of mass mm, moving with a speed 2υ0, collides inelasticaly (e>0) with an identical ball at rest. Show that (a) For head - on collision, both the balls move forward.
(b) For a genergcollision, the angle between the two velocities of scattered balls is less that 90∘.
View Solution