A car of mass M is accelerating on a level smooth road under the action of a single force F acting along the direction of motion. The power delivered to the car is constant and equal to p. If the velocity of the car at an instant is v, then after travelling a distance of the velocity become kv where k is__________.
The correct Answer is:2
To solve the problem, we need to find the value of k such that after traveling a distance of 7Mv33P, the velocity of the car becomes kv. We know that the power delivered to the car is constant and equal to P.
1. Understanding Power and Force Relation:
The power P delivered to the car can be expressed as:
P=F⋅v
where F is the force acting on the car and v is its velocity.
2. Expressing Force:
The force F can be related to acceleration a using Newton's second law:
F=M⋅a
where M is the mass of the car.
3. Relating Acceleration to Velocity:
The acceleration a can be expressed in terms of velocity v and displacement s as:
a=dvdt=dvds⋅v
Thus, we can write:
F=M⋅dvds⋅v
4. Substituting Force in Power Equation:
Substituting F in the power equation gives:
P=M⋅dvds⋅v2
5. Rearranging the Equation:
Rearranging the equation for dvds:
dvds=PMv2
6. Integrating the Equation:
We need to integrate this expression with respect to s from 0 to 7Mv33P and with respect to v from v to kv:
∫kvvdv=∫7Mv33P0PMv2ds
7. Calculating the Left Side:
The left side integrates to:
k−1
8. Calculating the Right Side:
The right side becomes:
PM∫kvv1v2dv=PM(−1v)kvv=PM(−1kv+1v)=PM(1−kkv)
9. Setting the Two Sides Equal:
Equating both sides gives:
k−1=PM⋅1−kkv
10. Solving for k:
After simplifying, we can solve for k:
k−1=(1−k)PMv
Rearranging and solving this equation leads us to find that k=2.
Final Answer:
Thus, the value of k is:
2
The power P delivered to the car can be expressed as:
P=F⋅v
where F is the force acting on the car and v is its velocity.
The force F can be related to acceleration a using Newton's second law:
F=M⋅a
where M is the mass of the car.
The acceleration a can be expressed in terms of velocity v and displacement s as:
a=dvdt=dvds⋅v
Thus, we can write:
F=M⋅dvds⋅v
Substituting F in the power equation gives:
P=M⋅dvds⋅v2
Rearranging the equation for dvds:
dvds=PMv2
We need to integrate this expression with respect to s from 0 to 7Mv33P and with respect to v from v to kv:
∫kvvdv=∫7Mv33P0PMv2ds
The left side integrates to:
k−1
The right side becomes:
PM∫kvv1v2dv=PM(−1v)kvv=PM(−1kv+1v)=PM(1−kkv)
Equating both sides gives:
k−1=PM⋅1−kkv
After simplifying, we can solve for k:
k−1=(1−k)PMv
Rearranging and solving this equation leads us to find that k=2.
Thus, the value of k is:
2
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:Level - 1 PARAGRAPH QUESTIONS
Explore 3 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2
Explore 48 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 0 - LONG ANSWER TYPE
Explore 5 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
A car of mass m is accelerating on a level smooth road under the action of a single F. The power delivered to the car is constant and equal to P. If the velocity of the car at an instant is v, then after travelling how much distance it becomes double?
 .
.
View SolutionA car of mass m starta from rest and accelerates so that the instyantaneous power delivered to the car has a constant magnitude P0. The instaneous velocity of this car is proportional to
View SolutionA car of mass m is driven with acceleration a along a straight level road against a constant external resistive force R. When the velocity of the car V, the rate at which the engine of the car is doing work will be
View SolutionA car of mass m is driven with acceleration a along a straight level road against a constant external resistive force R. When the velocity of the car V, the rate at which the engine of the car is doing work will be
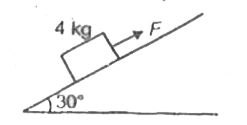
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
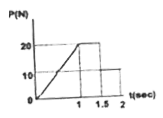
View SolutionA body of mass 6.25kg is travelling in a horizontal straight line with a velocity of 3m/ sec when a horizontal force P is applied to it at right angle to the initial direction of motion. If P varies according to the accompanying graph, remains constant in direction and is the only force acting on the body in its plane of motion,find the magnitude of the velocity of the body when t=2 sec.
View SolutionA toy car can deliver a constant power of 20W. The resistive force on the car is αv, where v is velocity of car in m/s. If maximum velocity of car is 2m/s, the value of α is .
View SolutionAB is a quarter of smooth circular track of radius R=6m. A particle P of mass 0.5kg moves along the track from A to B under the action of the following forces.
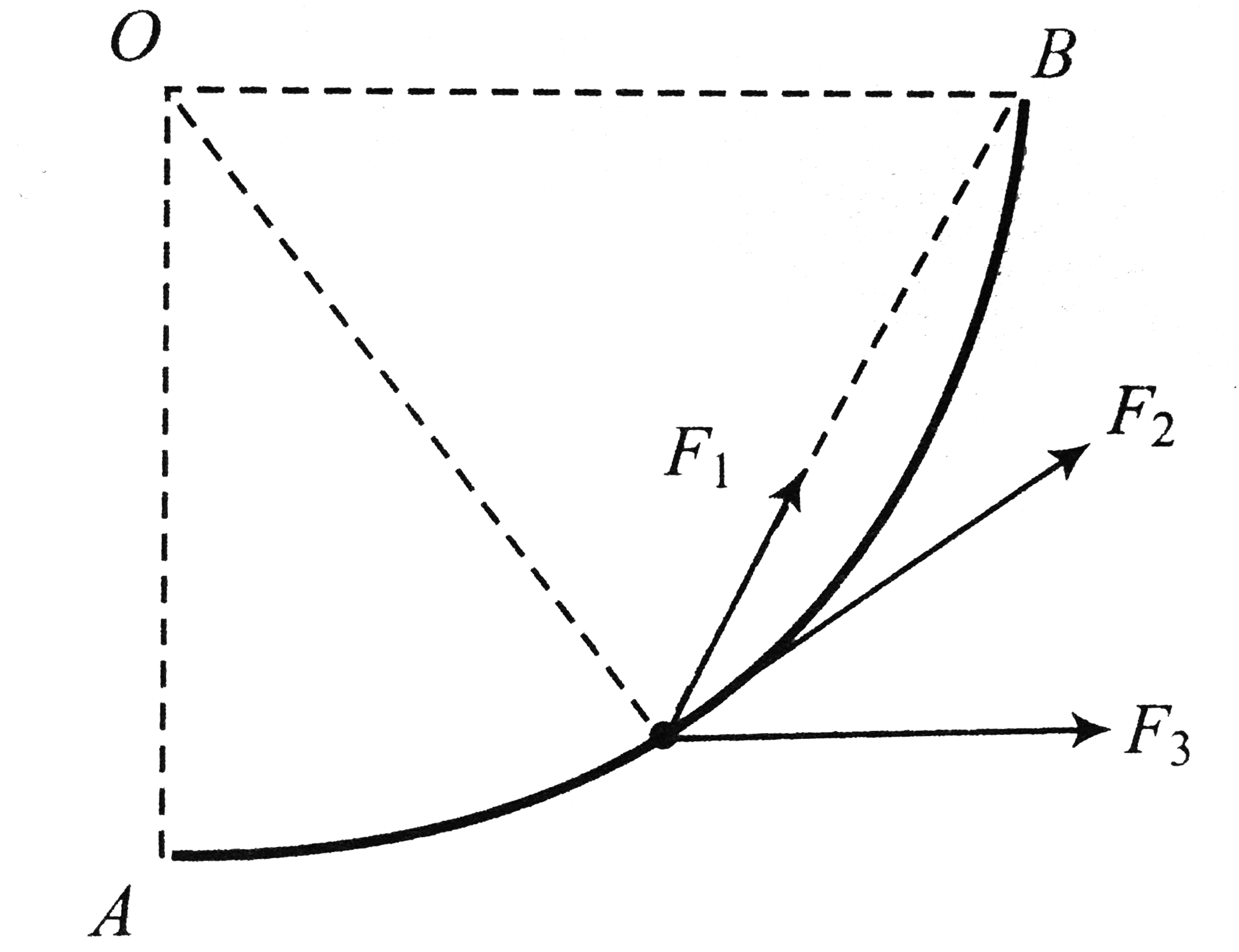
a. A force F1 directed always towards the point B, its magnitude is constant and is equal to 20N.
b. A force F2 directed along the instantaneous tangent to the circular track, its magnitude is (15−10S)N, where S is the distance travelled in metre.
c. A horizontal force of magnitude 30N.
Find the work done by forces mentioned in (a), (b) and (c)
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionThe word fluid means a substance having particles which readily of its magnitude (a small shear stress, which may appear to be of negligible will cause deformation in the fluid). Fluids are charactrised by such properties as density. Specific weight, specific gravity, viscosity etc. Density of a substance is defined as mass per unit volume and it is denoted by. The specific gravity represents a numerical ratio of two densities, and water is commonly taken as a reference substance. Specific gravity of a substance in written as the ratio of density of substance to the density of water. Specific weight represents the force exerted by gravity on a unit volume of fluid. It is related to the density as the product of density of a fluid and acceleration due to gravity. Viscosity is the most important and is recognized as the only single property which influences the fluid motion to a great extent. The viscosity is the property by virtue of which a fluid offers resistance to deformation under the influenece if shear force. The force between the layers opposing relative motion between them are known as forces of viscosity. When a boat moves slowly on the river remains at rest. Velocities of different layers are different. Let v be the velocity of the level at a distance y from the bed and V+dv be the velocity at a distance y+dy. The velocity differs by dv in going through a distance by perpendicular to it. The quantity dvdy is called velocity gradient. The force of viscosity between two layers of a fluid is proportional to velocity gradient and Area of the layer.
F∝A & F∝dvdy
F=−ηAdvdy (−ve sign shown the force is frictional in nature and opposes relative motion. η coefficient of dynamic viscosity
Shear stress FA=−ηdvdy
and simultaneously kinematic viscosity is defined as the dynamic viscosity divided by the density. If is denoted as v. The viscosity of a fluid depends upon its intermolecular structure. In gases, the molecules are widely spaced resulting in a negligible intermolecular cohesion, while in liquids the molecules being very close to each other, the cohesion is much larger with the increases of temperature, the cohesive force decreases rapidly resulting in the decreases of viscosity. In case of gases, the viscosity is mainly due to transfer of molecular momentum in the transerve direction brought about by the molecular agitation. Molecular agitation increases with rise in temperature. Thus we conclude that viscosity of a fluid may thus be considered to be composed of two parts, first due to intermolecuar cohesion and second due to transfer of molecular momentum.
If the velocity profile is given by
v=23y−y2v is velocity in m/secy is in meter above the bad. Determine shear stress at y=0.15m, & η=0.863Ns/m2
View Solution