A force exerts an impulse I on a particle changing its speed from u to 2u. The applied force and the initial velocity are oppositely directed along the same line. The work done by the force is
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have a particle that changes its speed from u to 2u under the influence of a force that is acting in the opposite direction to its initial velocity. We need to find the work done by this force in terms of the impulse I.
Step 2: Use the Work-Energy Theorem
According to the work-energy theorem, the work done W by the force is equal to the change in kinetic energy of the particle:
W=Kf−Ki
where Kf is the final kinetic energy and Ki is the initial kinetic energy.
Step 3: Calculate Initial and Final Kinetic Energies
The initial kinetic energy Ki when the speed is 2u is given by:
Ki=12m(2u)2=12m(4u2)=2mu2
The final kinetic energy Kf when the speed is u is given by:
Kf=12m(u)2=12mu2
Step 4: Calculate the Change in Kinetic Energy
Now, we can find the change in kinetic energy:
ΔK=Kf−Ki=12mu2−2mu2=12mu2−42mu2=−32mu2
Step 5: Substitute into the Work Equation
Thus, the work done by the force is:
W=−32mu2
Step 6: Relate Impulse to Change in Momentum
Impulse I is defined as the change in momentum. The initial momentum pi is:
pi=m(2u)=2mu
The final momentum pf is:
pf=mu
Thus, the impulse I is:
I=pf−pi=mu−2mu=−mu
Step 7: Express Work Done in Terms of Impulse
We can now express the work done in terms of the impulse:
Since I=−mu, we have:
−mu=I⟹mu=−I
Substituting this into the work done equation:
W=−32mu2=−32⋅(−I)⋅u=32Iu
Final Answer
Thus, the work done by the force is:
W=32Iu
We have a particle that changes its speed from u to 2u under the influence of a force that is acting in the opposite direction to its initial velocity. We need to find the work done by this force in terms of the impulse I.
According to the work-energy theorem, the work done W by the force is equal to the change in kinetic energy of the particle:
W=Kf−Ki
where Kf is the final kinetic energy and Ki is the initial kinetic energy.
The initial kinetic energy Ki when the speed is 2u is given by:
Ki=12m(2u)2=12m(4u2)=2mu2
Kf=12m(u)2=12mu2
Now, we can find the change in kinetic energy:
ΔK=Kf−Ki=12mu2−2mu2=12mu2−42mu2=−32mu2
Thus, the work done by the force is:
W=−32mu2
Impulse I is defined as the change in momentum. The initial momentum pi is:
pi=m(2u)=2mu
The final momentum pf is:
pf=mu
Thus, the impulse I is:
I=pf−pi=mu−2mu=−mu
We can now express the work done in terms of the impulse:
Since I=−mu, we have:
−mu=I⟹mu=−I
Substituting this into the work done equation:
W=−32mu2=−32⋅(−I)⋅u=32Iu
Thus, the work done by the force is:
W=32Iu
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:Level - 1 PARAGRAPH QUESTIONS
Explore 3 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2
Explore 48 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 0 - LONG ANSWER TYPE
Explore 5 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
A force exerts an impulse Ion a particle changing its speed from initial velocity u to final velocity 2u. The applied force and the initial velocity are oppositely oriented along the same line. The work done by the force is
View SolutionA force exerts an impulse Ion a particle changing its speed from initial velocity u to final velocity 2u. The applied force and the initial velocity are oppositely oriented along the same line. The work done by the force is
View SolutionCertain force acting on a 20 kg mass changes its velocity from 5m/s→2m/s. calculate the work done by the force.
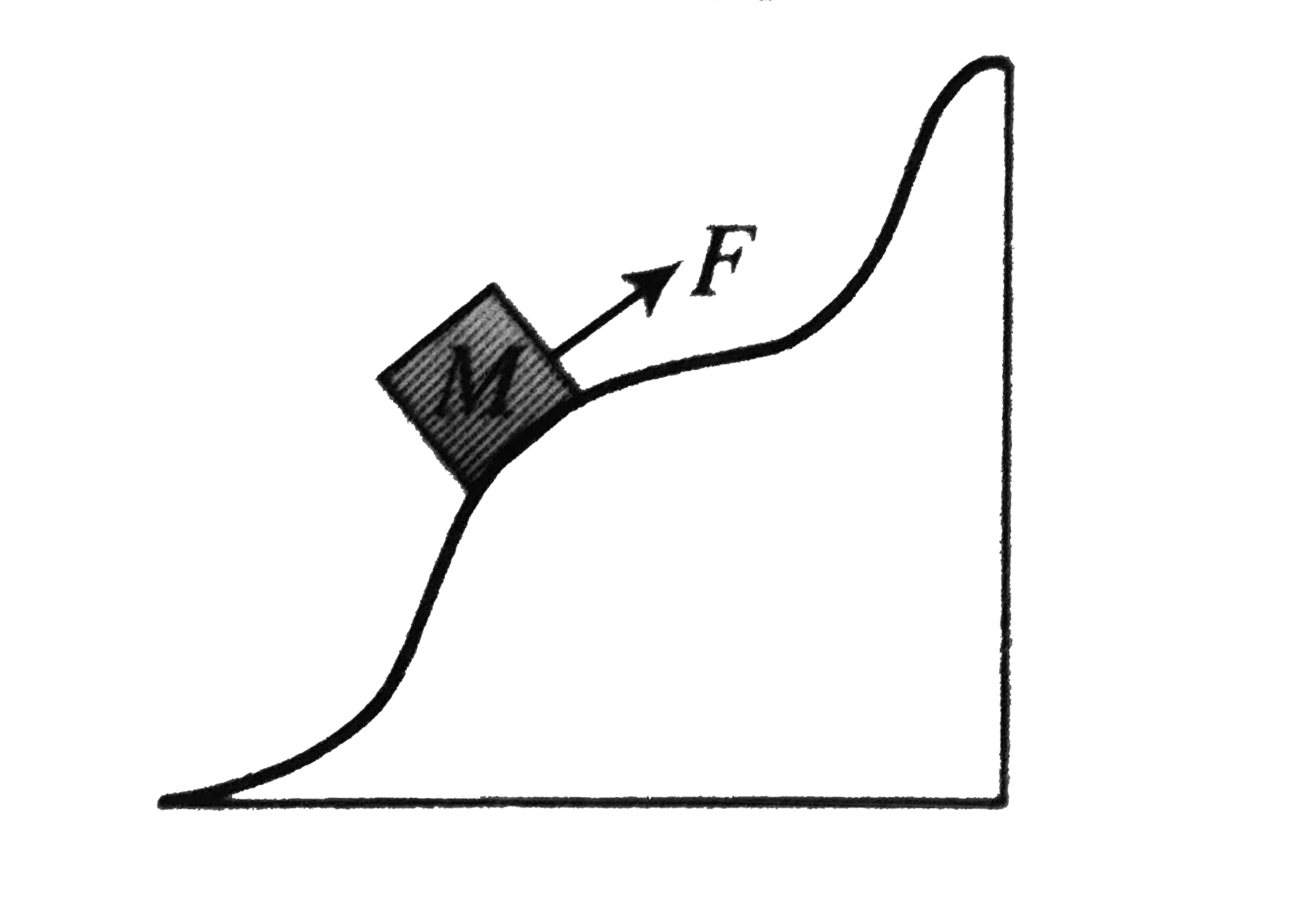
View SolutionA body of mass M was slowly hauled up a rough hill by a force F which at each point was directed along a tangent to the hill. Work done by the force
View SolutionForces acting on a particle moving in a straight line varies with the velocity of the particle as F=αυ where α is constant. The work done by this force in time interval Δt is :
View SolutionAn electron enters an electric field with its velocity in the direction of the electric lines of force. Then
View SolutionThe work done by a force →F during a displacement →r is given by →F.→r. Suppose a force of 12 N acts on a particle in vertically upward directionand the particle is displaced through 2.0 m in vertically downward direction. Find the work done by the force during this displacement.
View SolutionThe work done by a force →F during a displacement →r is given by →F.→r. Suppose a force of 12 N acts on a particle in vertically upward directionand the particle is displaced through 2.0 m in vertically downward direction. Find the work done by the force during this displacement.
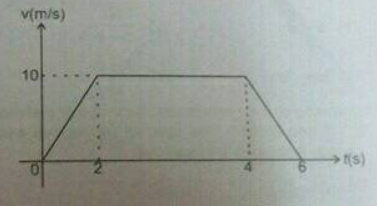
View SolutionA particle of mass 1 kg is moved under the action of a force and velocity time graph of the particle is shown in figure.Work done by the force from t=0 to t=6 s Is
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View Solution