Forces acting on a particle moving in a straight line varies with the velocity of the particle as F=αυ where α is constant. The work done by this force in time interval Δt is :
The correct Answer is:C
To find the work done by the force acting on a particle moving in a straight line, where the force varies with the velocity of the particle as F=αv, we can follow these steps:
1. Identify the Relationship Between Force and Power:
The power P delivered by a force F acting on a particle moving with velocity v is given by:
P=F⋅v
2. Substitute the Expression for Force:
Substitute F=αv into the power equation:
P=(αv)⋅v=α
This shows that the power is constant and equal to α.
3. Relate Power to Work Done:
The power can also be expressed as the rate of change of work done W:
P=dWdt
Therefore, we can equate the two expressions for power:
dWdt=α
4. Integrate to Find Work Done:
To find the total work done W over a time interval Δt, we integrate both sides:
W=∫Δt0αdt
5. Evaluate the Integral:
The integral of a constant α over the time interval from 0 to Δt is:
W=α∫Δt0dt=α(t)Δt0=α(Δt−0)=αΔt
6. Final Result:
Thus, the work done by the force in the time interval Δt is:
W=αΔt
The power P delivered by a force F acting on a particle moving with velocity v is given by:
P=F⋅v
Substitute F=αv into the power equation:
P=(αv)⋅v=α
This shows that the power is constant and equal to α.
The power can also be expressed as the rate of change of work done W:
P=dWdt
Therefore, we can equate the two expressions for power:
dWdt=α
To find the total work done W over a time interval Δt, we integrate both sides:
W=∫Δt0αdt
The integral of a constant α over the time interval from 0 to Δt is:
W=α∫Δt0dt=α(t)Δt0=α(Δt−0)=αΔt
Thus, the work done by the force in the time interval Δt is:
W=αΔt
Similar Questions
Force acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionKinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
View SolutionIf average velocity of particle moving on a straight line is zero in a time interval, then
View SolutionThe velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is 2kg. Work done by all the forces acting on the particle in time interval between t=0 to t=10s is

View SolutionThe force F acting on a particle is moving in a straight line as shown in figure. What is the work done by the force on the particle in the 4 m of the trajectory?
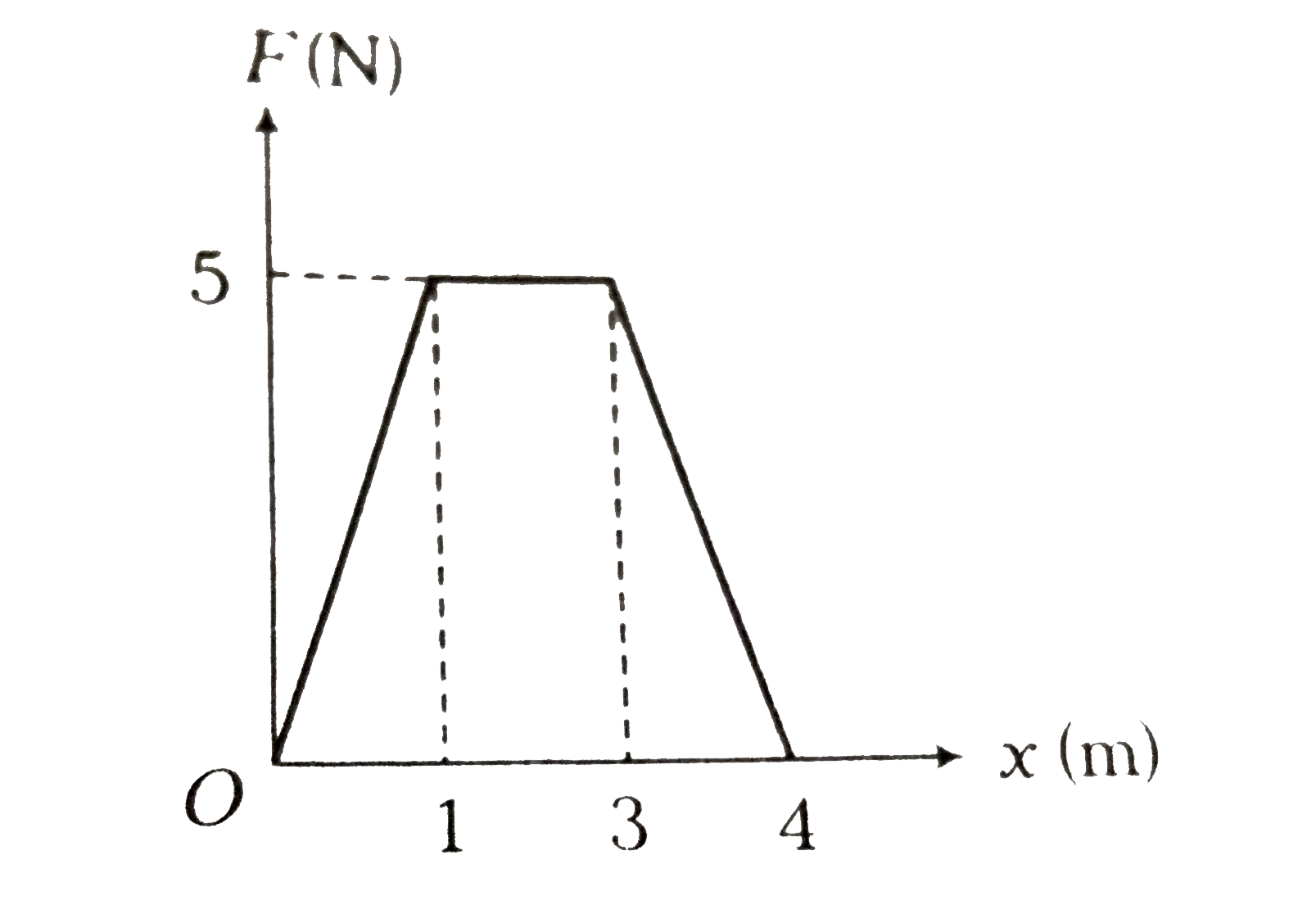
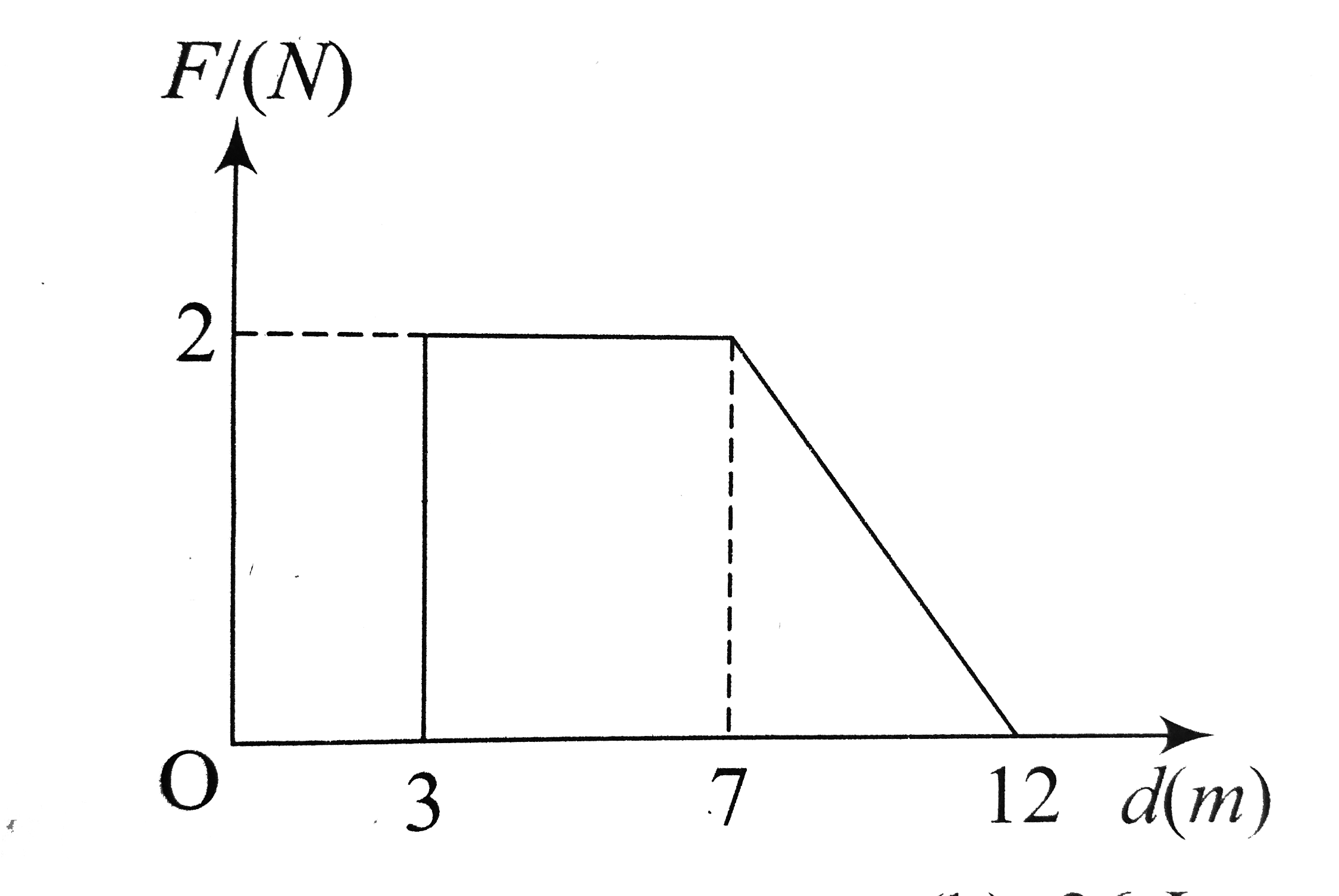
View SolutionForce F on a particle moving in a straight line varies with distance d as shown in the figure. The work done on the particle during its displacement of 12m is
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with displacement as x1K. Find the value of K.
View SolutionKinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
View SolutionThe force acting on a particle moving along a straight line varies with time as shown in diagram.
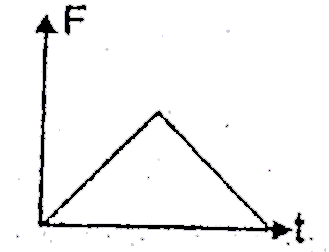
Which of the following graphs is best representative of its speed and time graphs. Initial velocity the particle is zero.
View Solution

