The power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
√x
x
x2
x1/3
The correct Answer is:D
To solve the problem of how the velocity of a particle varies with displacement when the power supplied by a force is constant, we can follow these steps:
1. Understanding Power:
The power (P) supplied by a force acting on a particle can be expressed in two ways:
P=Wt=F⋅v
where W is work, t is time, F is force, and v is velocity.
2. Relating Power to Force and Velocity:
Since the power is constant, we can write:
P=F⋅v
Rearranging gives us:
F=Pv
3. Using Newton's Second Law:
According to Newton's second law, force can also be expressed as:
F=m⋅a
where m is mass and a is acceleration.
4. Acceleration in Terms of Velocity and Displacement:
We know that acceleration a can be expressed in terms of velocity v and displacement x using the relation:
a=vdvdx
5. Substituting for Force:
By substituting F in terms of P and v into the equation from Newton's second law, we have:
Pv=m⋅vdvdx
6. Rearranging the Equation:
Rearranging gives:
P=mv2dvdx
7. Separating Variables:
We can separate variables to integrate:
dvv2=Pmdx
8. Integrating Both Sides:
Integrating both sides:
−1v=Pmx+C
where C is the integration constant.
9. Solving for Velocity:
Rearranging gives:
v=−1Pmx+C
However, we need to express v in terms of x in a more usable form.
10. Finding the Relationship:
To find how v varies with x, we can assume that C can be adjusted based on initial conditions. For large values of x, the term C becomes less significant, leading to:
v∝x1/3
Final Result:
Thus, the velocity of the particle varies with displacement x as:
v∝x1/3
The power (P) supplied by a force acting on a particle can be expressed in two ways:
P=Wt=F⋅v
where W is work, t is time, F is force, and v is velocity.
Since the power is constant, we can write:
P=F⋅v
Rearranging gives us:
F=Pv
According to Newton's second law, force can also be expressed as:
F=m⋅a
where m is mass and a is acceleration.
We know that acceleration a can be expressed in terms of velocity v and displacement x using the relation:
a=vdvdx
By substituting F in terms of P and v into the equation from Newton's second law, we have:
Pv=m⋅vdvdx
Rearranging gives:
P=mv2dvdx
We can separate variables to integrate:
dvv2=Pmdx
Integrating both sides:
−1v=Pmx+C
where C is the integration constant.
Rearranging gives:
v=−1Pmx+C
However, we need to express v in terms of x in a more usable form.
To find how v varies with x, we can assume that C can be adjusted based on initial conditions. For large values of x, the term C becomes less significant, leading to:
v∝x1/3
Thus, the velocity of the particle varies with displacement x as:
v∝x1/3
Similar Questions
The power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with displacement as x1K. Find the value of K.
View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (S) as a=2S. The velocity of the particle is zero and zero displacement. Find the corresponding velocity-displacement equation.
View Solution
Knowledge Check
Force F on a particle moving in a straight line varies with distance d as shown in figure
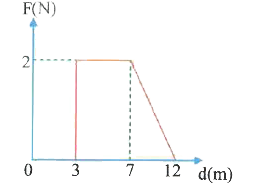
The work done on the particle during its displacement of 12 m isA18JB21JC26JD13JDisplacement time graph of a particle moving in a straight line is a shown in figure.
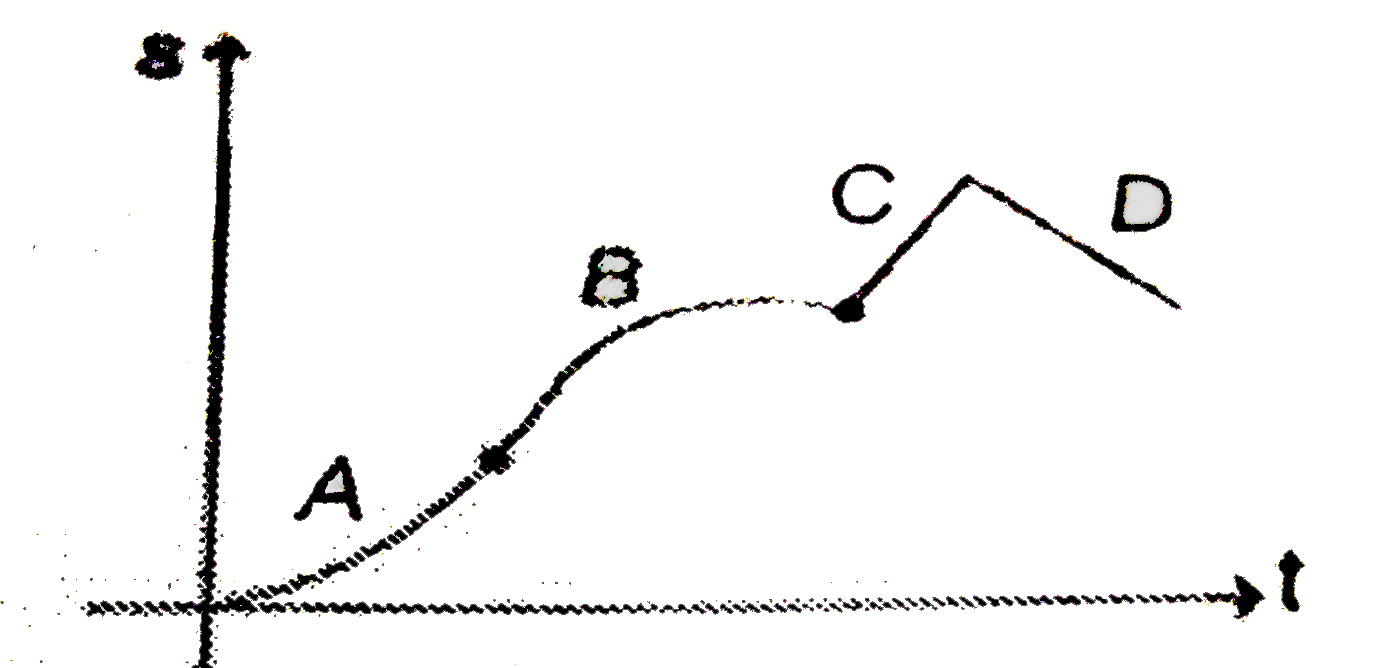 Ain region A acceleration is positiveBin region B acceleration is negativeCin region C acceleration is positiveDin region D acceleration is negative
Ain region A acceleration is positiveBin region B acceleration is negativeCin region C acceleration is positiveDin region D acceleration is negativeForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
A√ktmB√2ktmC2√ktmDnone of these
The acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
View SolutionAcceleration v/s displacement graph of a particle moving in a straight line is as shown in the figure. The initial velocity of the particle is zero. The velocity v/s displacement graph of the particle would be :

View SolutionForces acting on a particle moving in a straight line varies with the velocity of the particle as F=αυ where α is constant. The work done by this force in time interval Δt is :
View SolutionForces acting on a particle moving in a straight line varies with the velocity of the particle as F=αυ where α is constant. The work done by this force in time interval Δt is :
View SolutionVelocity versus displacement graph of a particle moving in a straight line as shown in figure.

The acceleration of the particle.
View Solution

