The acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
To solve the problem step by step, we need to derive the velocity-displacement equation from the given acceleration-displacement relationship. The acceleration a is given as:
a=2s+1
where s is the displacement.
Step 1: Relate acceleration to velocity and displacement
We know that acceleration a can be expressed as:
a=dvdt
Using the chain rule, we can rewrite this as:
a=dvds⋅dsdt=dvds⋅v
where v=dsdt is the velocity.
Step 2: Substitute the expression for acceleration
Substituting the expression for acceleration into the equation gives us:
dvds⋅v=2s+1
Step 3: Rearranging the equation
We can rearrange this equation to isolate dv:
vdv=(2s+1)ds
Step 4: Integrate both sides
Now we integrate both sides. The left side integrates with respect to v and the right side with respect to s:
∫vdv=∫(2s+1)ds
The left side becomes:
v22
And the right side becomes:
s2+s
Thus, we have:
v22=s2+s+C
where C is the constant of integration.
Step 5: Determine the constant of integration
Given that the velocity v=0 when the displacement s=0, we can substitute these values to find C:
022=02+0+C⟹C=0
Step 6: Final equation
Substituting C back into the equation gives:
v22=s2+s
Multiplying through by 2 to eliminate the fraction results in:
v2=2s2+2s
This can be factored as:
v2=2s(s+1)
Taking the square root gives us the final velocity-displacement equation:
v=√2s(s+1)
Summary of the Solution
The corresponding velocity-displacement equation is:
v=√2s(s+1)
We know that acceleration a can be expressed as:
Substituting the expression for acceleration into the equation gives us:
We can rearrange this equation to isolate dv:
Now we integrate both sides. The left side integrates with respect to v and the right side with respect to s:
Given that the velocity v=0 when the displacement s=0, we can substitute these values to find C:
Substituting C back into the equation gives:
The corresponding velocity-displacement equation is:
Topper's Solved these Questions
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-1
6 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-2
7 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Integer Type Question
3 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - SUBJECTIVE QUESTION
9 Videos
Similar Questions
The acceleration (a) of a particle moving in a straight line varies with its displacement (S) as a=2S. The velocity of the particle is zero and zero displacement. Find the corresponding velocity-displacement equation.
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
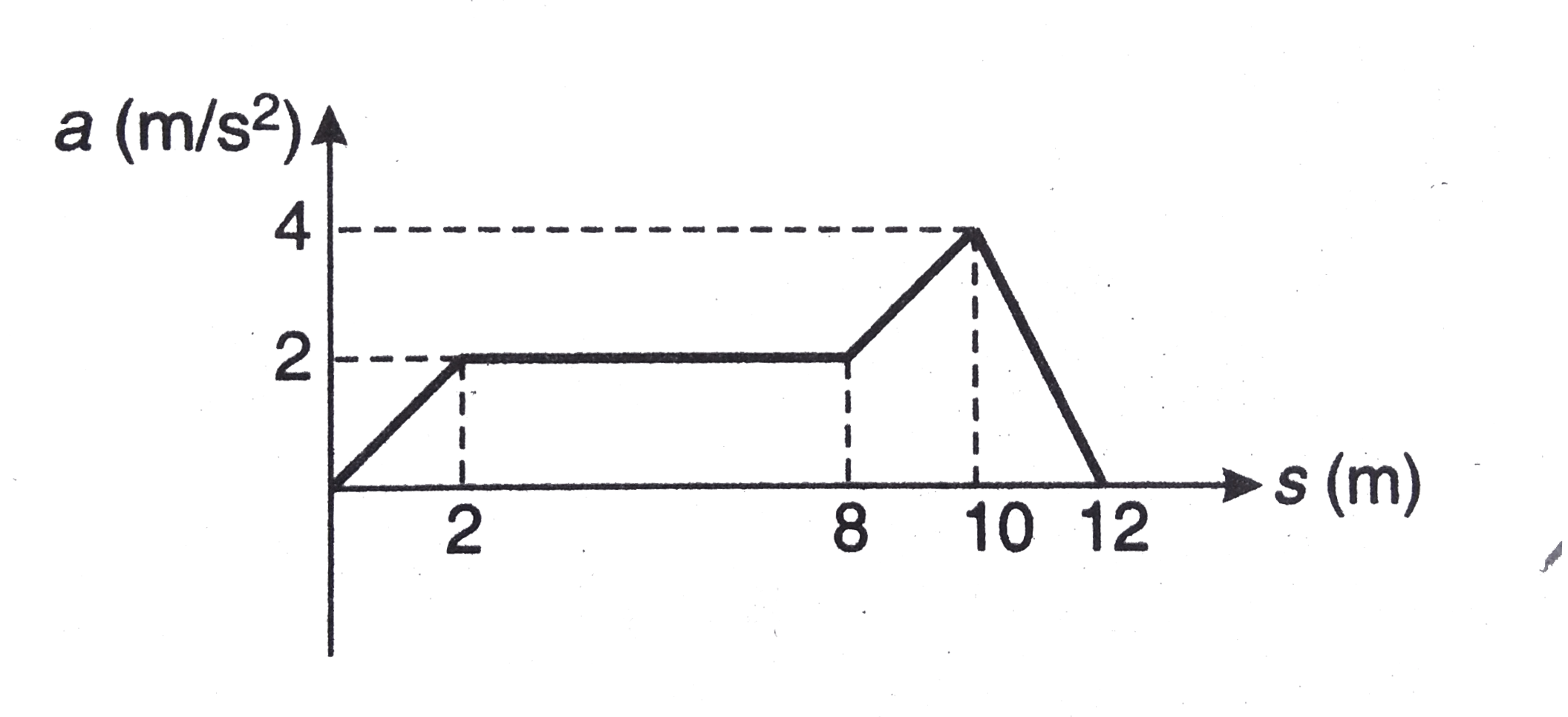
View Solution
Knowledge Check
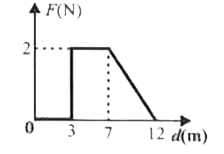
Force F on a particle moving in a straight line varies with distance d as shown in figure
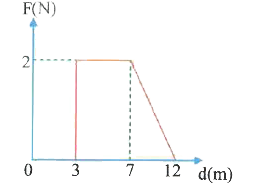
The work done on the particle during its displacement of 12 m isA18JB21JC26JD13JDisplacement time graph of a particle moving in a straight line is a shown in figure.
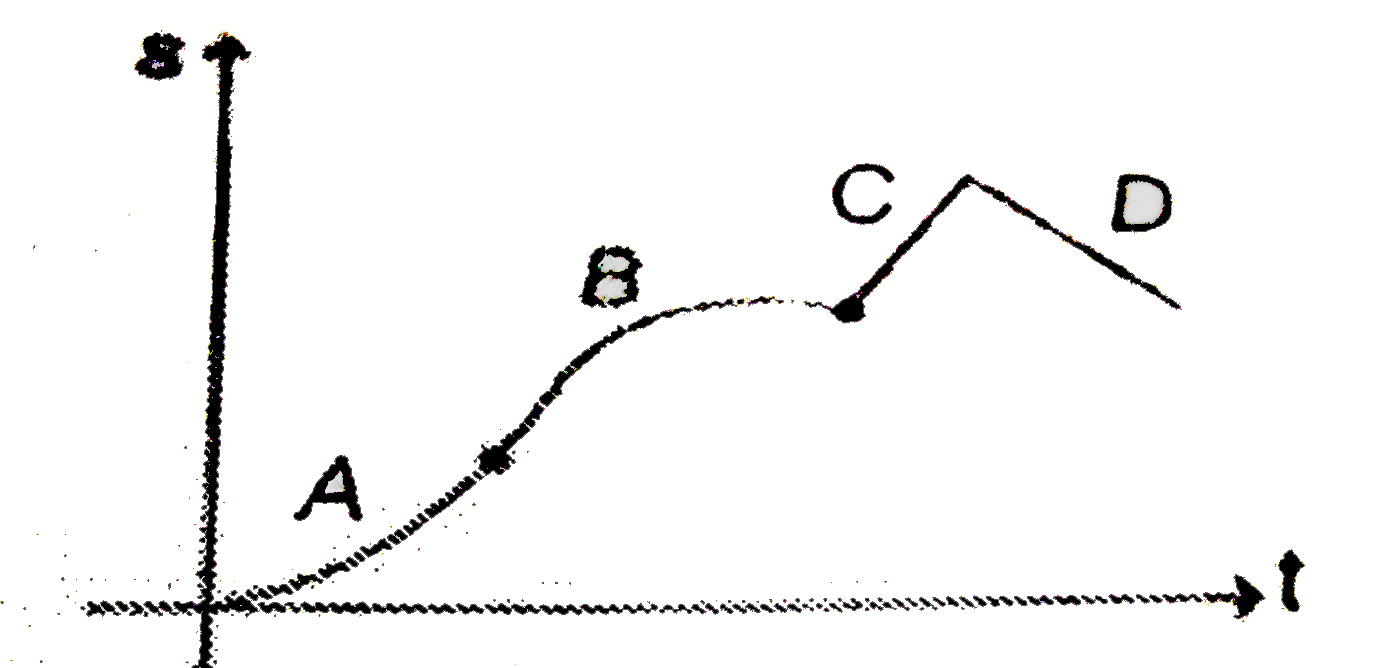 Ain region A acceleration is positiveBin region B acceleration is negativeCin region C acceleration is positiveDin region D acceleration is negative
Ain region A acceleration is positiveBin region B acceleration is negativeCin region C acceleration is positiveDin region D acceleration is negativeThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
A√xBxCx2Dx1/3
Velocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionForce F on a particle moving in a straight line varies with distance d as shown is figure. The work done on the particle during its displacement of 10 m is :-
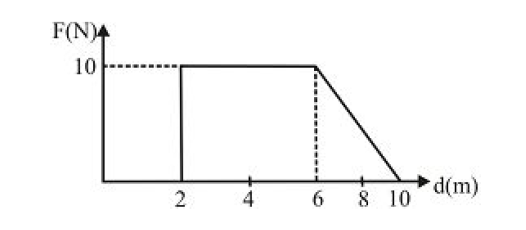
View SolutionFor a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
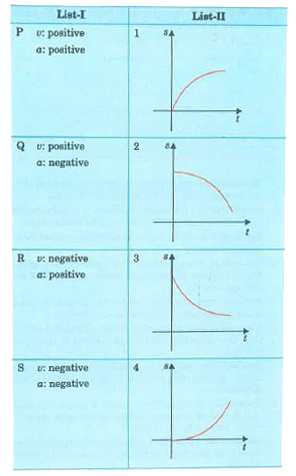
View SolutionForce F on a particle moving in a straight line varies with distance d as shown in figure. The work done on the particle during its displacement of 12 m is
View SolutionThe figure shows a velocity-time graph of a particle moving along a straight line
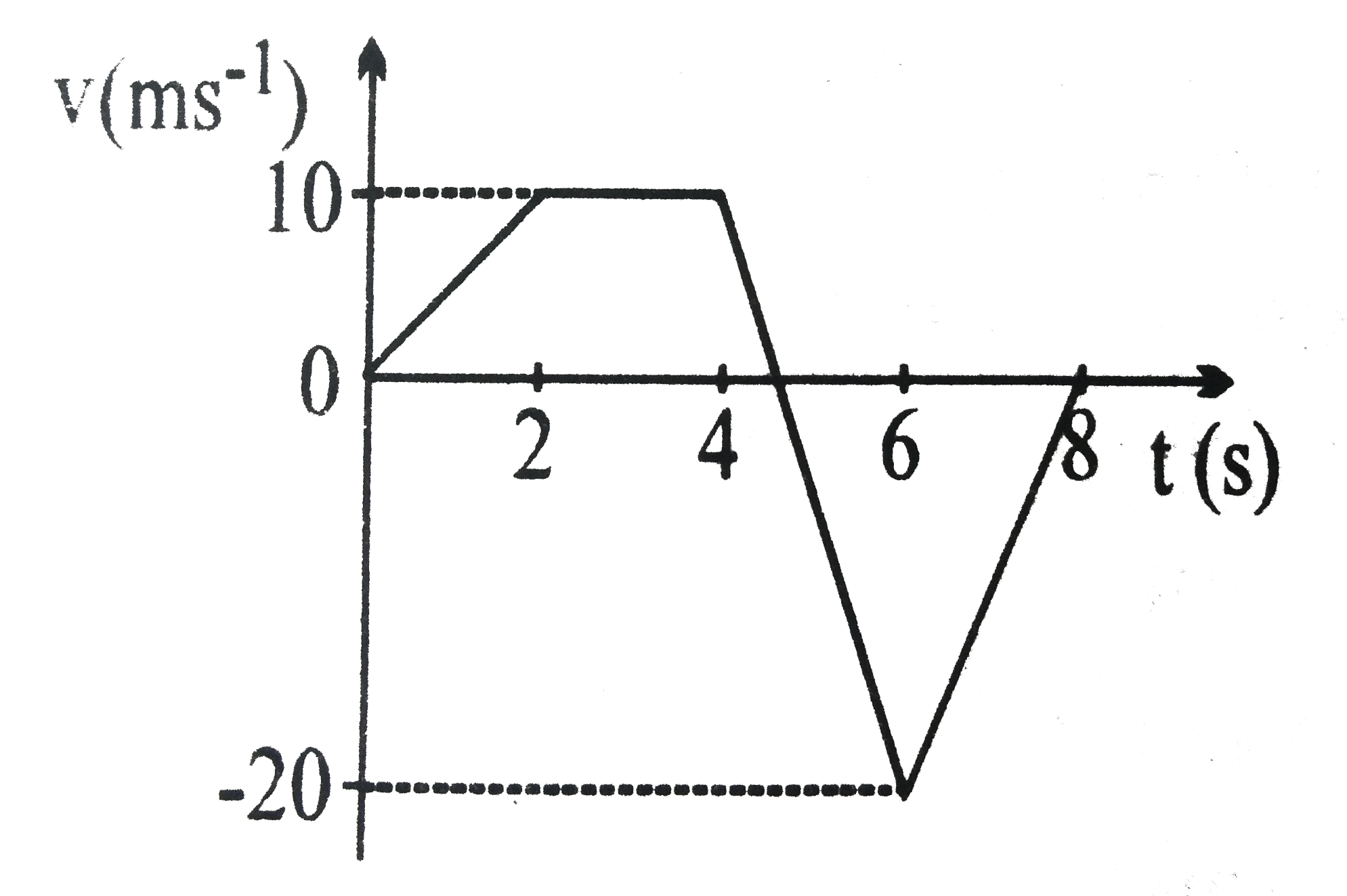
The maximum displacement of the particle is
View Solution
