A ball moving along a straight line collides elastically with another stationary ball of the same mass. At the moment of collision, the angle between the straight line passing through the centres of the balls and the direction of tr initial motion of the striking ball is θ, find the fraction of the kinetic energy of the striking ball converted into potential energy at the moment of the maximum deformation.
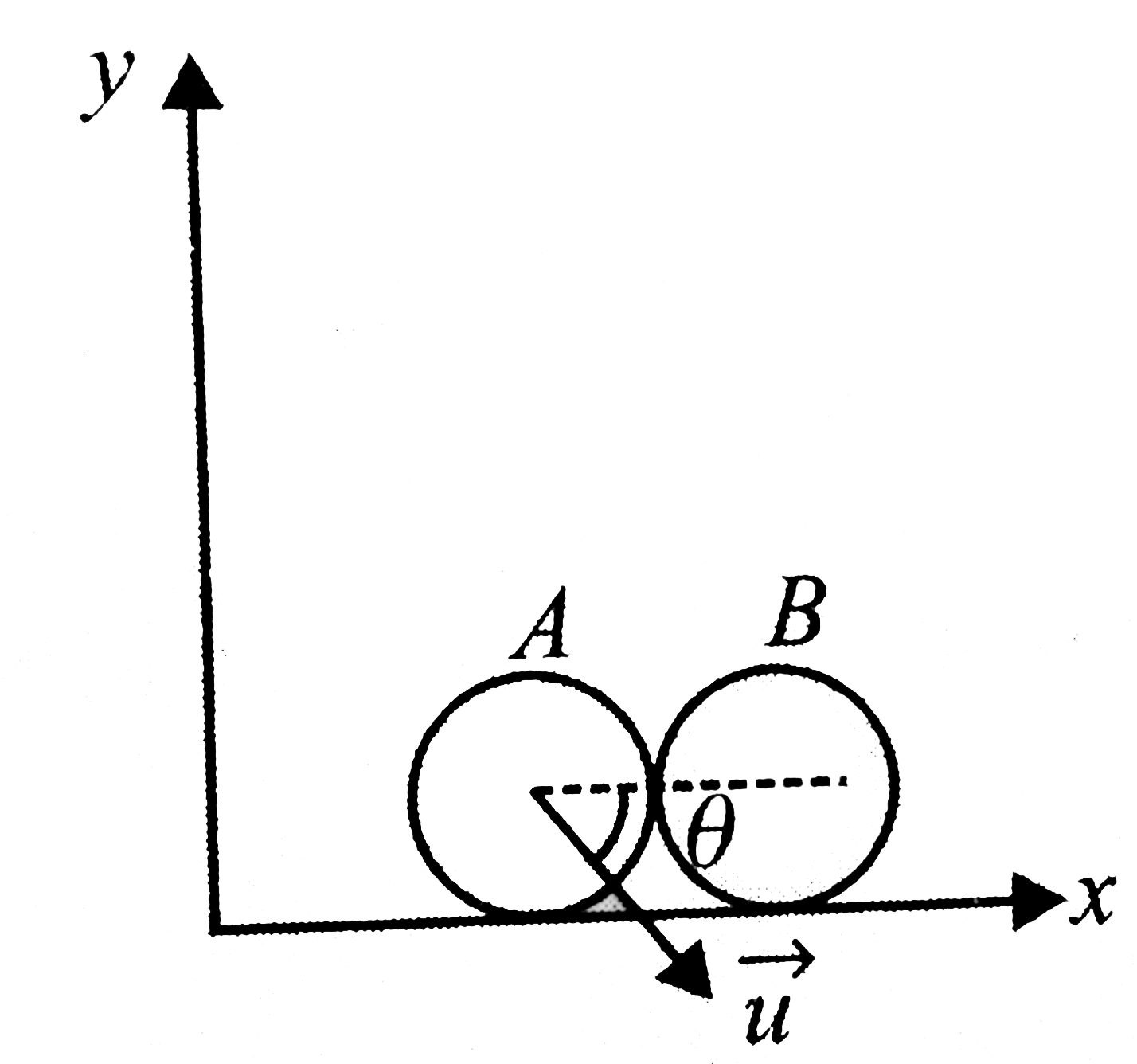
Let a ball A of mass m moving with velocity →v collide with stationary ball B as shown in figure. As there is no external force, the linear momentum is conserved. As collision is two dimentional, the x and y components of the linear momentum are separately conserved.

Let →v1 and →v2 be the velocities of the particle after collision.
Then conservation of linear momentum along x - axis gives
mucosθ=mv1x+mv2x
⇒v1x+v2x=ucosθ..........i
and conservation of linear momentum along y-axis gives
mucosθ=mv1x+mv2y
⇒v1y+v2y=usinθ............ii ltbr> at the moment of maximum deformation
⇒v1xy=v2x=ucosθ2 [using eqn i ]
and the tangential velocities iof balls before and after collision should be equal.
usinθ=v1y and v2y=0
Initial KEEi=12mu2
Final KE
Ef=12mv21x+12mv21y+12mv22x+12mv22y
=12m(v21x+v22x)+12mv21y+2mv22y
mv21x+12mv21y+0 (since v1x=v2x)
=m(ucosθ2)2+12m(usinθ)2
=14mu2cos2θ+12mu2sin2θ
=12mu2{12cos2θ+sin2θ}
=12mu2{cos2θ+sin2θ−12cos2θ}
=12mu2{1−12cos2θ}
Fraction of KE converted into PE at the moment of maximum deformation
f=Ei−EfEi=12μ2−12mu2(1−cos2θ2)12μ2=cos2θ2
Here θ=45∘,
∴f=cos245∘2=14=0.25
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Consider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
View SolutionA ball of mass 5 kg moving with speed 8 m/s collides head on with another stationary ball of mass 15 kg. If collision is perfectly inelastic, then loss in kinetic energ is
View Solution
Knowledge Check
A ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is k. If radius of the ball be R, then the fraction of total energy associated with its rotation will be.
Ak2+R2R2Bk2R2Ck2k2+R2DR2k2+R2
A ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
View SolutionA ball of mass m moving at a speed v makes a head on inelastic collision with an identical ball at rest. The kinetic energy of the balls after the collision is 34th of the original. Find the coefficient of restitution.


View SolutionA ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is k. If radius of the ball be R, then the fraction of total energy associated with its rotation will be.
View SolutionA ball of mass 1kg moving with 4m−1 along +x-axis collides elastically with an another ball of mass 2kg moving with 6m/s is opposite direction. Find their velocities after collision.
View SolutionA ball of mass 2kg moving with speed 5m/s collides directly with another ball of mass 3kg moving in the same direction with speed 4m/s. The coefficient of restitution is 2/3. Find the velocities of both ball after the collision.
View SolutionA ball of mass m is projected with a speed v into the barrel of a spring gun of mass M initially at rest lying on a frictionless surface. The mass sticks in the barrel at the point of maximum compression in the spring. The fraction of kinetic energy of the ball stored in the spring is
View SolutionTwo identical billiard balls undergo an oblique elastic collision. Initially, one of the balls is stationary. If the initially stationary ball after collision moves in a direction which makes an angle of 37∘ with direction of initial motion of the moving ball, then the angle through which initially moving ball will be deflected is
View Solution