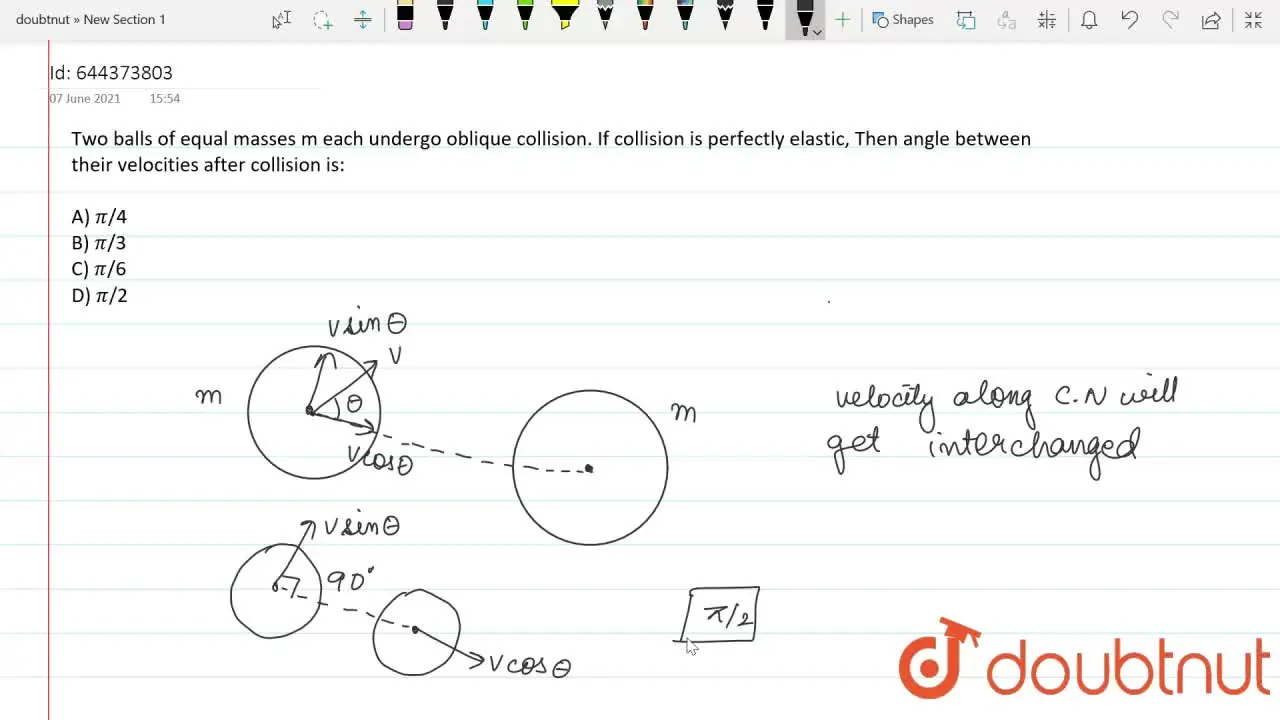
Two balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
π4
π3
π6
π2
The correct Answer is:D
Step by step video & image solution for Two balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)64videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)35videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)14videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
Two balls each of mass 2kg (one at rest) undergo oblique collision is perfectly elastic, then the angle between their velocities after collision is
View SolutionBlock A has a mass 3kg and is sliding on a rough horizontal surface with a velocity uA=2m/s when it makes a direct collision with block B, which has a mass of 2kg and is originally at rest. The collision is perfectly elastic. Determine the velocity of each block just after collision and the distance between the blocks when they stop sliding. The coefficient of kinetic friction between the blocks and the plane is μk=0.3 ( Take g=10m/s2)
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionConsider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
View SolutionTwo balls roll toward each other. The red ball has a mass of 0.5 kg and a speed of 4m/s just before impact. The green ball has a mass of 0.3 kg and a speed of 2 m/s. if the collision is perfectly inelastic, determine the velocity of the composite object after the collision.
View SolutionTwo particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.
 View Solution
View SolutionA ball of mass m moving horizontally at a speed v collides with the bob of a simple pendulum at rest. The mass of the bob is also m. If the collision is perfectly elastic and both balls sticks, the height to which the two balls rise after the collision will be given by:
View SolutionA particle (a mud pallet, say) of mass m strikes a smooth stationary wedge of mass M with as velocity v0 at an angle θ with horizontal. If the collision is perfectly inelastic, find the
a. velocity of the wedge just after the collision.
b. Change in KE of the system (M+m) in collision. View Solution
View SolutionAn object is moving towards a mirror with a velocity of 10ms−1 as shown in the figure. If the collision between the mirror and the object is perfectly elastic, then the velocity of the image after collision with mirror in vector form is
 View Solution
View Solution