A transverse sinusoidal wave moves along a string in the positive x-direction at a speed of 10cm/s. The wavelength of the wave is 0.5 m and its amplitude is 10cm. At a particular time t,the snapshot of the wave is shown in figure. The velocity of point P when its displacement is 5 cm is

(a) √3π50ˆjm/s
(b)−√3π50ˆjm/s
(c)√3π50ˆim/s
(d) −√3π50ˆim/s
√3π50ˆjm/s
−√3π50ˆjm/s
√3π50ˆim/s
−√3π50ˆim/s
The correct Answer is:5
Aeq=√A21+A22+2A1A2cosϕ
Aeq=√42+32+2(4)(3)cosπ2
Aeq=5.
Topper's Solved these Questions
Similar Questions
A travelling wave in a string has speed 5 cm/s in -ve x direction its amplitude is 10 mm and wavelength 1 m. At a particular time a point P has displacement 5√3 mm. Find the velocity vector of point P ?
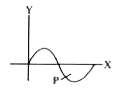
View SolutionFigure shows a snapshot of a sinusoidal travelling wave taken at t=0.3s.The wavelength is 7.5cm and the amplitude is 2cm. If the crest P was at x=0at t=0, write the equation of travelling wave. ,

View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
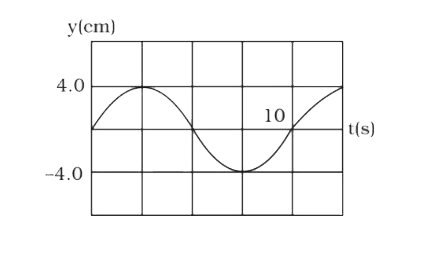
Q. The velocity of propagation of the wave is ?
View SolutionA sinusoidal wave trsvelling in the positive direction on a stretched string has amplitude 2.0cm, wavelength 1.0m and velocity 5.0m/s. At x=0 and t=0 it is given that y=0 and ∂y∂t<0. Find the wave function y(x,t).
View SolutionFigure shows a wave pulse at t=0. The pulse moves to the right with a speed of 10cms^-1. Sketch the shape of the string at t=1s, 2s and 3s.

View SolutionA sinusoidal wave is traveling on a string with speed 40 cm/s. The displacement of the particle of the string at x = 10 cm varies with time according to
y = (5.0cm) sin(1.0−4.0s−1)t)The linear density of the string is 4.0 g/cm
View SolutionConsider a sinusoidal travelling wave shown in figure. The wave velocity is +40cm/s.
Find
(a) the frequency
(b) the phase difference between points 2.5cm apart
(c) the velocity of a particle at P at the instant shown.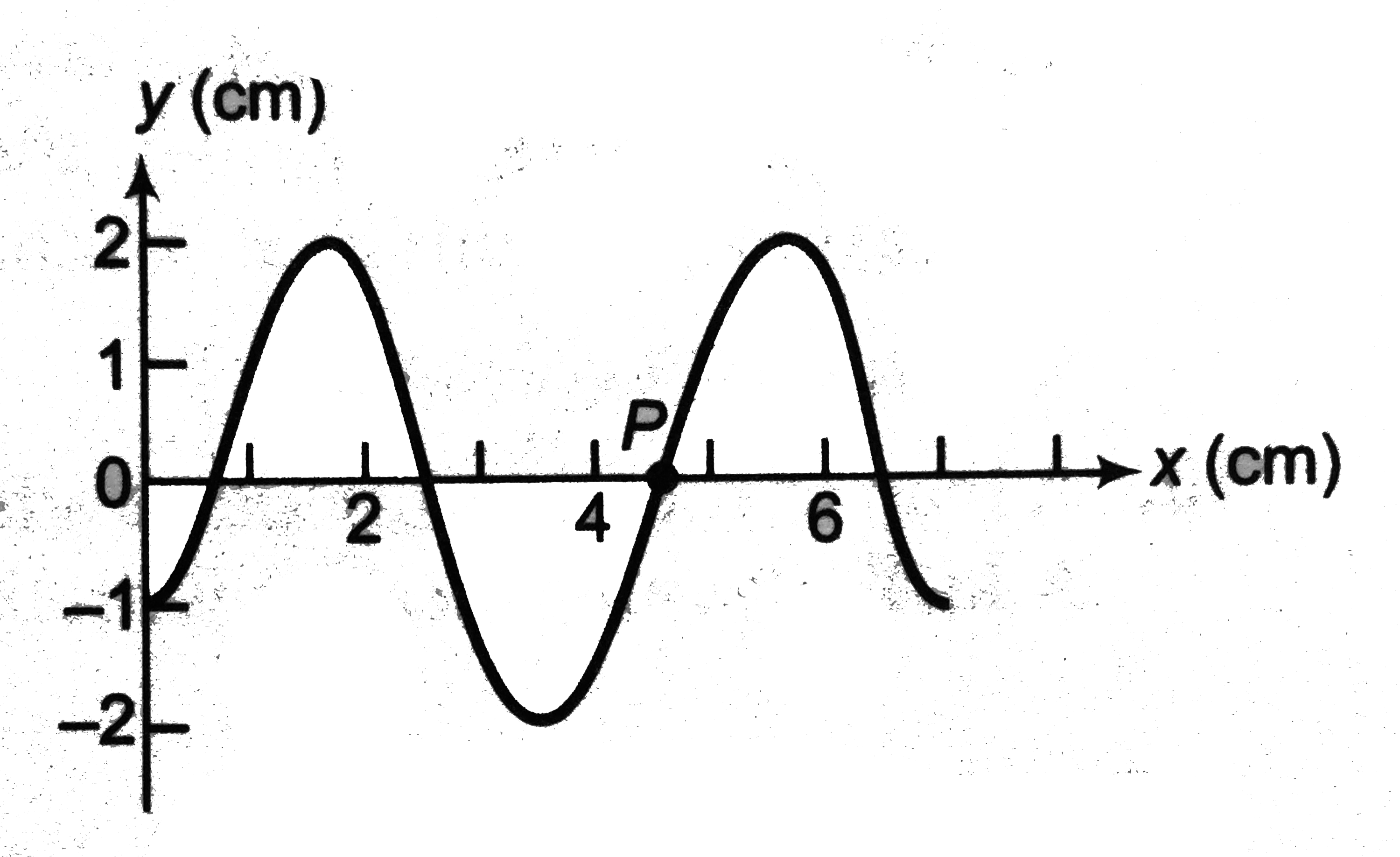
View SolutionShape of a string transmitting wave along x-axis some instant is shown. Velocity of point P v - (4π)cm /s (θ) = tan−1(0.004pi)
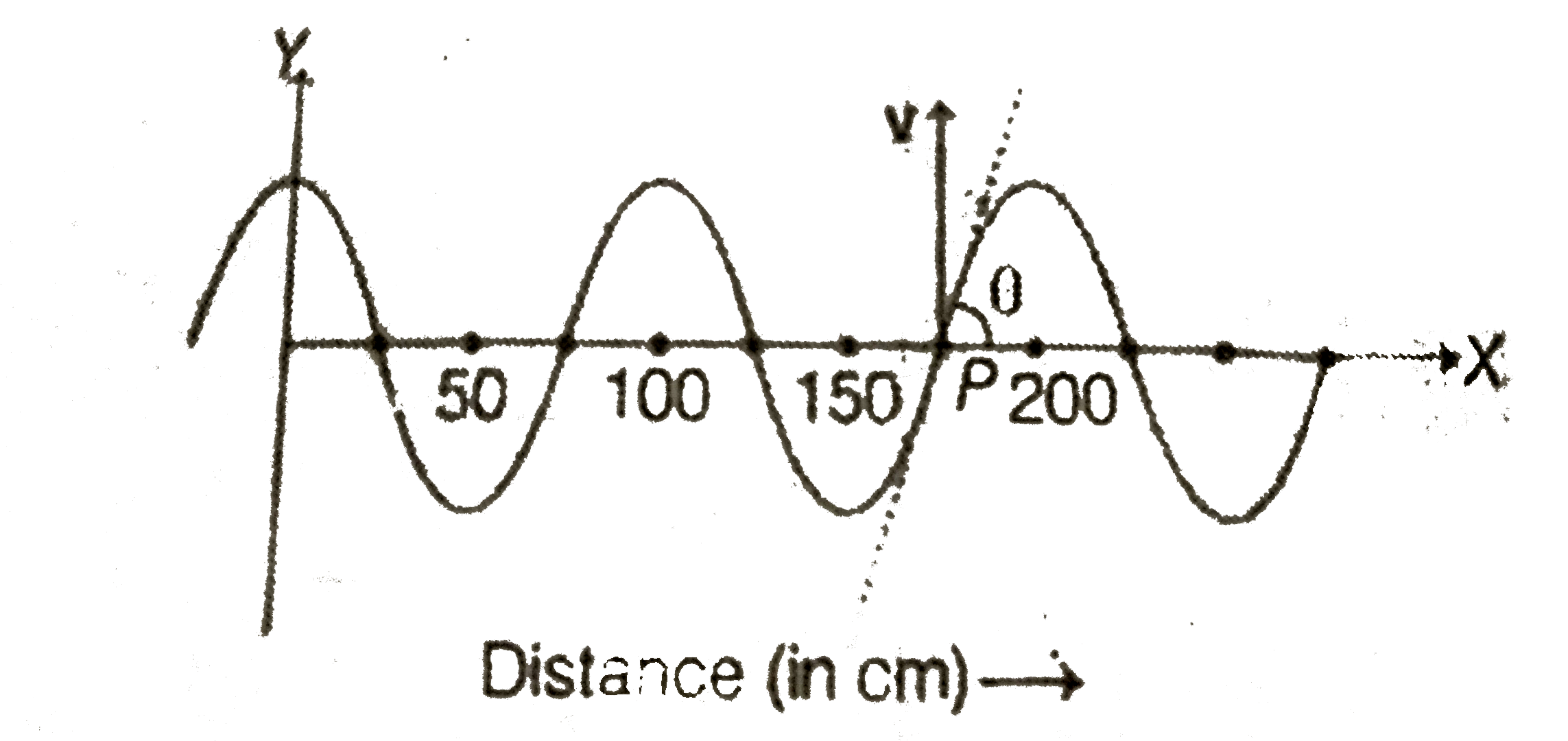
View SolutionThe displacement wave in a string is y=(3cm)sin6.28(0.5x−50t) where x is in centimetres and t in seconds. The velocity and wavelength of the wave is :-
View SolutionA transverse wave of wavelength 50 cm is travelling towards+vex-axis along a string whose linear density is 0.05g/cm. The tension in the string is 450 N. At t=0,the particle at x=0 is passing through its mean position wave. The amplitude of the wave is 2.5 cm.
View Solution

