A transverse wave of wavelength 50 cm is travelling towards+vex-axis along a string whose linear density is 0.05g/cm. The tension in the string is 450 N. At t=0,the particle at x=0 is passing through its mean position wave. The amplitude of the wave is 2.5 cm.
To solve the problem step by step, we will derive the parameters of the transverse wave based on the given information.
Step 1: Convert units
First, we need to convert the given values into standard SI units.
- Wavelength (λ) = 50 cm = 0.5 m
- Linear density (μ) = 0.05 g/cm = 0.05 × 10^-3 kg/cm = 0.05 × 10^-3 × 100 = 0.005 kg/m
- Amplitude (A) = 2.5 cm = 0.025 m
Step 2: Calculate wave number (k)
The wave number (k) is given by the formula:
k=2πλ
Substituting the value of λ:
k=2π0.5=4πrad/m
Step 3: Calculate the velocity of the wave (v)
The velocity of the transverse wave in the string is given by:
v=√Tμ
Where T is the tension in the string. Substituting the values:
v=√450N0.005kg/m=√90000=300m/s
Step 4: Calculate angular frequency (ω)
The angular frequency (ω) is related to the frequency (f) and can be calculated using the wave velocity (v) and wavelength (λ):
f=vλ
Substituting the values:
f=300m/s0.5m=600Hz
Now, we can find ω:
ω=2πf=2π×600=1200πrad/s
Step 5: Determine the phase constant (φ₀)
At t=0 and x=0, the particle is at its mean position, which means:
y(0,0)=Asin(k⋅0−ω⋅0+ϕ0)=0
This implies:
sin(ϕ0)=0
Thus, ϕ0=nπ where n is an integer. Since the wave is moving in the positive x-direction and the particle is at the mean position, we can take ϕ0=0 or ϕ0=π.
To determine which one, we can analyze the velocity:
From the velocity equation:
v=−Aωcos(kx−ωt+ϕ0)
At t=0 and x=0:
v(0,0)=−Aωcos(ϕ0)
Since the particle is moving upwards (positive direction), we need cos(ϕ0)>0, thus ϕ0=0.
Step 6: Write the wave equation
Now we can write the general equation of the wave:
y(x,t)=Asin(kx−ωt+ϕ0)
Substituting the values we found:
y(x,t)=0.025sin(4πx−1200πt+0)
Final Answer:
The equation of the wave is:
y(x,t)=0.025sin(4πx−1200πt)
---
First, we need to convert the given values into standard SI units.
- Linear density (μ) = 0.05 g/cm = 0.05 × 10^-3 kg/cm = 0.05 × 10^-3 × 100 = 0.005 kg/m
- Amplitude (A) = 2.5 cm = 0.025 m
The wave number (k) is given by the formula:
k=2πλ
Substituting the value of λ:
k=2π0.5=4πrad/m
The velocity of the transverse wave in the string is given by:
v=√Tμ
Where T is the tension in the string. Substituting the values:
v=√450N0.005kg/m=√90000=300m/s
The angular frequency (ω) is related to the frequency (f) and can be calculated using the wave velocity (v) and wavelength (λ):
f=vλ
Substituting the values:
f=300m/s0.5m=600Hz
ω=2πf=2π×600=1200πrad/s
At t=0 and x=0, the particle is at its mean position, which means:
y(0,0)=Asin(k⋅0−ω⋅0+ϕ0)=0
This implies:
sin(ϕ0)=0
Thus, ϕ0=nπ where n is an integer. Since the wave is moving in the positive x-direction and the particle is at the mean position, we can take ϕ0=0 or ϕ0=π.
From the velocity equation:
v=−Aωcos(kx−ωt+ϕ0)
At t=0 and x=0:
v(0,0)=−Aωcos(ϕ0)
Since the particle is moving upwards (positive direction), we need cos(ϕ0)>0, thus ϕ0=0.
Now we can write the general equation of the wave:
y(x,t)=Asin(kx−ωt+ϕ0)
Substituting the values we found:
y(x,t)=0.025sin(4πx−1200πt+0)
The equation of the wave is:
y(x,t)=0.025sin(4πx−1200πt)
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Example
9 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.1
9 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
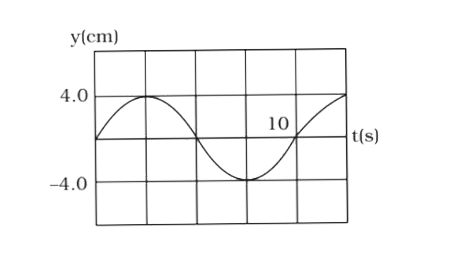
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.

Q. The velocity of propagation of the wave is ?
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. The transverse displacement of the string particle at as a function of time is shown in Figure.
The equation of the wave with all the constants evaluated is:
View SolutionA 100 Hz sinusoidal wave is travelling in the positve x - direaction along a string with a linear mass density of 3.5×10−3kgm−1 and a tension of 35 N. At time t =0 ,the point x=0 has zero displacment and the slope of the string is π/20then select the wrong alternative.
View SolutionA transverse sine wave of amplitude 10 cm and wavelength 200 cm travels from left to right along a long horizontal stretched, string with a speed of 100 cm/s. Take the origin at left end of the string. At time t = 0 the left end of the string is at the origin and is moving downward. Then the equation of the wave will be ( in CGS system )
View SolutionA transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
View SolutionCalculate the velocity of a transverse wave along a string of length 2m and mass 0.06kg under a tension of 500N.
View SolutionOne end of a long string of linear mass dnesity 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256 Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0 the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describest the wave on the string.
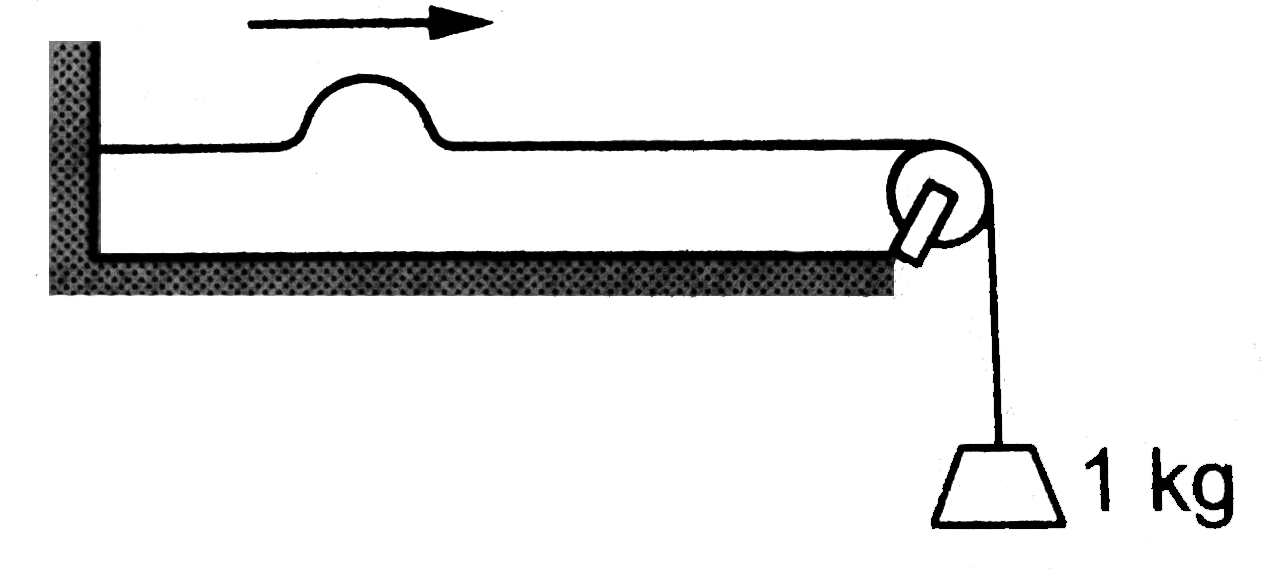
View SolutionFigure showa a string of linear mass density 1.0gcm−1onwhichawaveps–eistravell∈g.F∈dthetimetakenbytheps–e∈travell∈gthroughadistanceof50cmonthestr∈g.Takeg=10 ms^-2.
View SolutionA certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

View SolutionA certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

View Solution
