A string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160Nm−1 and is stretched by 1.0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring ?
To solve the problem step by step, we will calculate the time taken for a wave pulse to travel along the string from the wall to the spring.
Step 1: Convert Units
First, we need to convert the given measurements into consistent units. The length of the string is given as 40 cm, which we can convert to meters:
L=40 cm=0.40 m
The mass of the string is given as 10 g, which we can convert to kilograms:
m=10 g=0.01 kg
The deflection of the spring is given as 1 cm, which we convert to meters:
x=1 cm=0.01 m
Step 2: Calculate Mass per Unit Length
Next, we calculate the mass per unit length (μ) of the string:
μ=mL=0.01 kg0.40 m=0.025 kg/m
Step 3: Calculate Tension in the String
The tension (T) in the string is provided by the spring, which can be calculated using Hooke's Law:
T=k⋅x
where k is the spring constant and x is the deflection. Substituting the values:
T=160 N/m⋅0.01 m=1.6 N
Step 4: Calculate the Velocity of the Wave
The velocity (v) of the wave on the string can be calculated using the formula:
v=√Tμ
Substituting the values we have:
v=√1.6 N0.025 kg/m=√64=8 m/s
Step 5: Calculate the Time Taken for the Pulse to Reach the Spring
Finally, we can calculate the time (t) taken for the wave pulse to travel the length of the string to the spring:
t=Lv=0.40 m8 m/s=0.05 s
Final Answer
The time taken for the wave pulse to reach the spring is:
0.05 seconds
---
First, we need to convert the given measurements into consistent units. The length of the string is given as 40 cm, which we can convert to meters:
L=40 cm=0.40 m
The mass of the string is given as 10 g, which we can convert to kilograms:
m=10 g=0.01 kg
The deflection of the spring is given as 1 cm, which we convert to meters:
x=1 cm=0.01 m
Next, we calculate the mass per unit length (μ) of the string:
μ=mL=0.01 kg0.40 m=0.025 kg/m
The tension (T) in the string is provided by the spring, which can be calculated using Hooke's Law:
T=k⋅x
where k is the spring constant and x is the deflection. Substituting the values:
T=160 N/m⋅0.01 m=1.6 N
The velocity (v) of the wave on the string can be calculated using the formula:
v=√Tμ
Substituting the values we have:
v=√1.6 N0.025 kg/m=√64=8 m/s
Finally, we can calculate the time (t) taken for the wave pulse to travel the length of the string to the spring:
t=Lv=0.40 m8 m/s=0.05 s
The time taken for the wave pulse to reach the spring is:
0.05 seconds
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Comprehension
45 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?

View SolutionA spring of spring constant 5×103N/m is stretched initially by 5 cm from the unstretched position. The work required to further stretch the spring by another 5 cm is .
View Solution
Knowledge Check
A string of mass 3 kg is under tension of 400 N. the length of the stretched string is 25 cm. if the transverse jerk is stuck at one end of the string how long does the disturbance take to reach the other end?
A0.043sB4.33SC0.055 sD0.034 sl=24+3.5m
One end of a spring is attached to a ceiling. When an object of mass m kilograms is attached to the other end of the spring, the spring stretches to a length of l centimeters as shown in the equation above. What is m when l is 73 ?A14B27.7C73D279.5
A 1m long rope, having a mass of 40g, is fixed at one end and is tied to a light string at the other end. The tension in the string in 400N. Find the wavelength in second overtone (in cm).
View SolutionOne end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
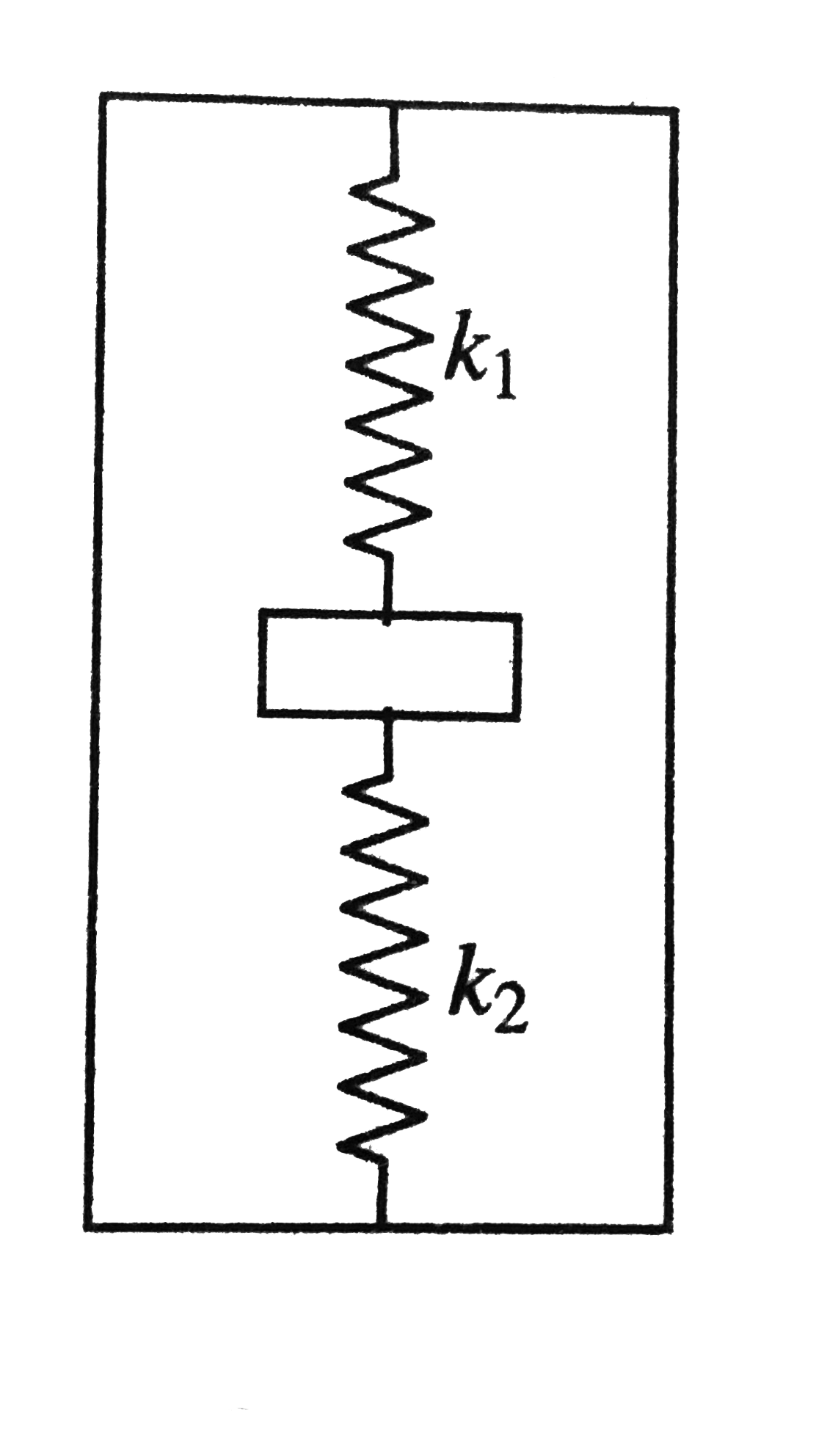
View SolutionTwo point masses of 3.0 kg and 1.0 kg are attached to opposite ends of a horizontal spring whose spring constant is 300Nm−1 as shown in the figure. The natural vibration frequency of the system is of the order of :

View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View SolutionWhen a 20 g mass hangs attached to one end of a light spring of length 10 cm, the spring stretches by 2 cm. The mass is pulled down until the total length of the spring is 14 cm. The elastic energy, (in Joule) stored in the spring is :
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
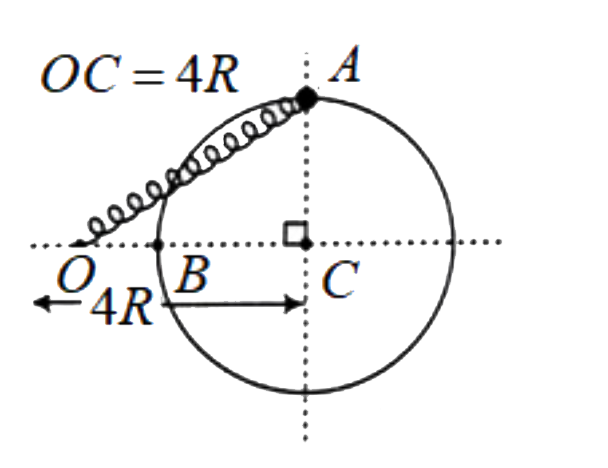
View Solution
