Question

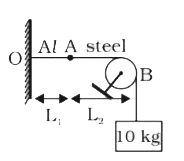
An aluminium wire of cross-sectional area ${\displaystyle \left({10}^{-6}\right)m^2}$ is joined to a steel wire of the same cross-sectional area. This compound wire is stretched on a sonometer pulled by a weight of 10kg. The total length of the compound wire between the bridges is 1.5m of which the aluminium wire is ${\displaystyle 0.6m}$ and the rest is steel wire. Transverse vibrations are setup in the wire by using an external source of variable frequency. Find the lowest frequency of excitation for which the standing waves are formed such that the joint in the wire is a node. What is the total number of nodes at this frequency? The density of aluminium is ${\displaystyle 2.6\times \left({10}^3\right)kg/m^3}$ and that of steel is ${\displaystyle 1.04\times {10}^{4}kg/m^2(g=10m/s^2)}$

Answer

`162` vibration//sec, `3`

Explanation

`A = 1 xx 10^(-6) m, T = 10g = 100N`
`sigma_(1) = 2.6 xx 10^(3)kg//m^(2) , sigma_(2) = 1.04 xx 10^(4) kg//m^(3)`
`v_(1) = sqrt(100/(1xx10^(6)xx1.04xx10^(3)))=(10^(3))/(sqrt(26))m//sec`
`V_(2)=sqrt(100/(1xx10^(-6)xx1.04xx10^(4)))=(10^(3))/(2sqrt(26))`
`f_(1)=f_(2)`
`(n_(1)xx10^(3))/(2 xx 0.6sqrt(26)) = (n_(2) xx 10^(3))/(2 xx 2 xx 0.9sqrt(26)) [(n_(1))/(n_(2)) = (1)/(3)]`
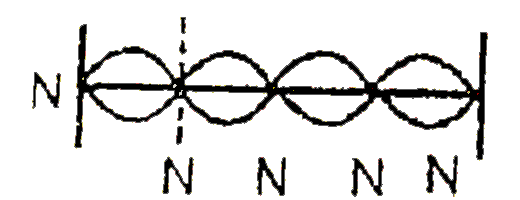
Lowest frequency `= (n_(1)v_(1))/(2L_(1)) = (1 xx 10^(3))/(sqrt(26) xx 2 xx 0.6)`
`= (10^(4))/(12sqrt(26)) = 162 "vibration"//"sec"`.
`(n_(1))/(n_(2)) = ((1)/(3))`
One side `1` loop and other side `3` loop
So excluding the two nodes at ends total nodes is `3`