A conducting frame abcd is kept in a vertical plane. A conducting rod of of mass m and length can slide smoothly on it remaining always horizontal. The resistance of the loop is negligible and inductance is constant having value . The rod is left from rest and allowed to fall under gravity and inductor has no initial current. A magnetic field of constant magnitude Bis present throughout the loop pointing inwards. Determine

(a) position of the rod as a function of time assuming initial position of the rod to be and vertically downward as the positive x-axis.
(b) the maximum current in the circuit.
(c) maximum velocity of the rod
The correct Answer is:A, B, C
..(i)
differentiating,...(ii)
From (i) & (ii)
Where
From (ii)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-3 PART 3
16 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View SolutionA conducting rod of length L slides at a constant velocity V on two parallel conducting rails as shown in figure. The mechanical power required to pull the rod at constant velocity is

View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionCDEF is a fixed conducting smooth frame in vertical plane. A conducting uniform rod GH of mass m can move vertically and smoothly without losing contact with the frame. Gh always remains horizontal and is given velocity u upward and released. Taking the acceleration due to gravity as g and present other than R. Find out the time tasken by the rod to reach the highest point.

View SolutionA uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?

View SolutionA thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=mg2q. The rod is released from, shown position from rest.

What is the angular acceleration of the rod at the instant of releasing the rod?
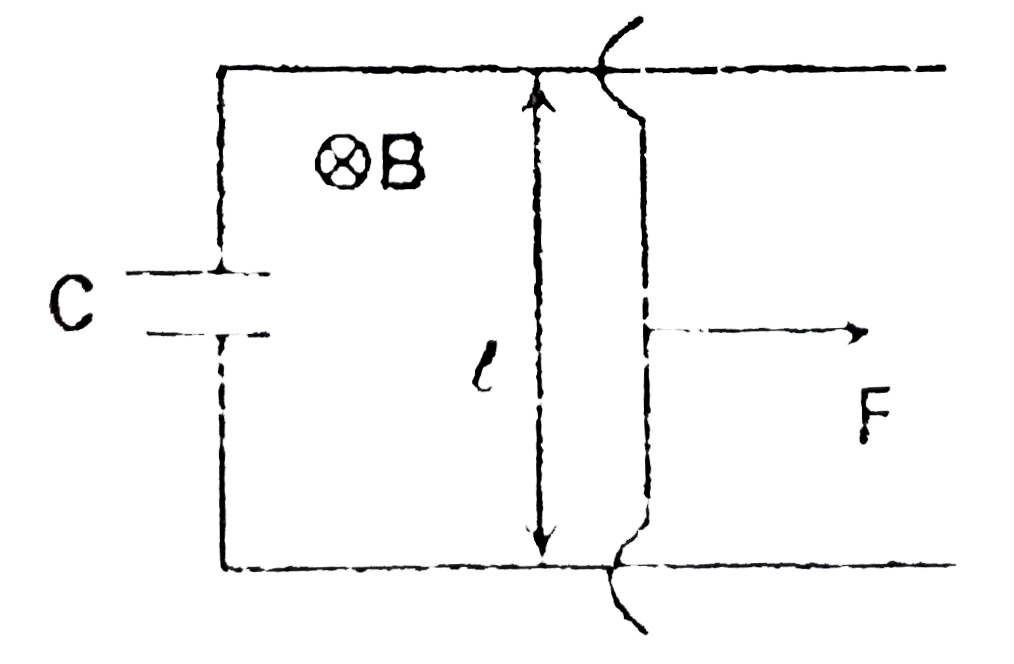
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. Whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
View Solution
