An infinitesimally small bar magnet of dipole moment M is moving with the speed v in the X-direction. A small closed circular conducting loop of radius 'a' and negligible self-inductance lies in the Y-Z plane with its centre x=0, and its axis coninding with the X-axis. Find the force opposing the motion of the magnet, if the resistance of the loop is R. Assume that the distance x of the magnet from the centre of the loop is much greater than a.
The correct Answer is:A, B, D
Given that x>>a
magnetic field at the centre of the coil due to the bar magnet is B=μ04π2Mx3=μ02πMx3
Due to this, magnetic flux linked with the coil will be- ϕ=BS=μ02πMx3(πa2)=μ0Ma22x3
∴ induced emf in the coil, due to motion of the magnet is e=−dϕdt=−(μ0Ma22)ddt(lx3)
=μ0Ma22(3X4)dxdt=32μ0Ma2Rx4V(dxdt=V)
Therefore, induced current in the coil is i=eR=32μ0Ma2VRx4
Potential energy of →M in →B will be U=−M'Bcos180∘
U=M'B
=32μ0πMa4VRx4(μ02π,Mx3)
U=34μ20M2a4VR1x7
∴F=−dUdx=214μ20M2a4VRx8
Positive sign of F implies that there will be a repulsion between the magnet and the coil. Note that here we cannot apply F=μ04π6MM'x4 (directly)...(i)
because here M is a funtion of x however equation (1) can be applied where M and M' both are constants.
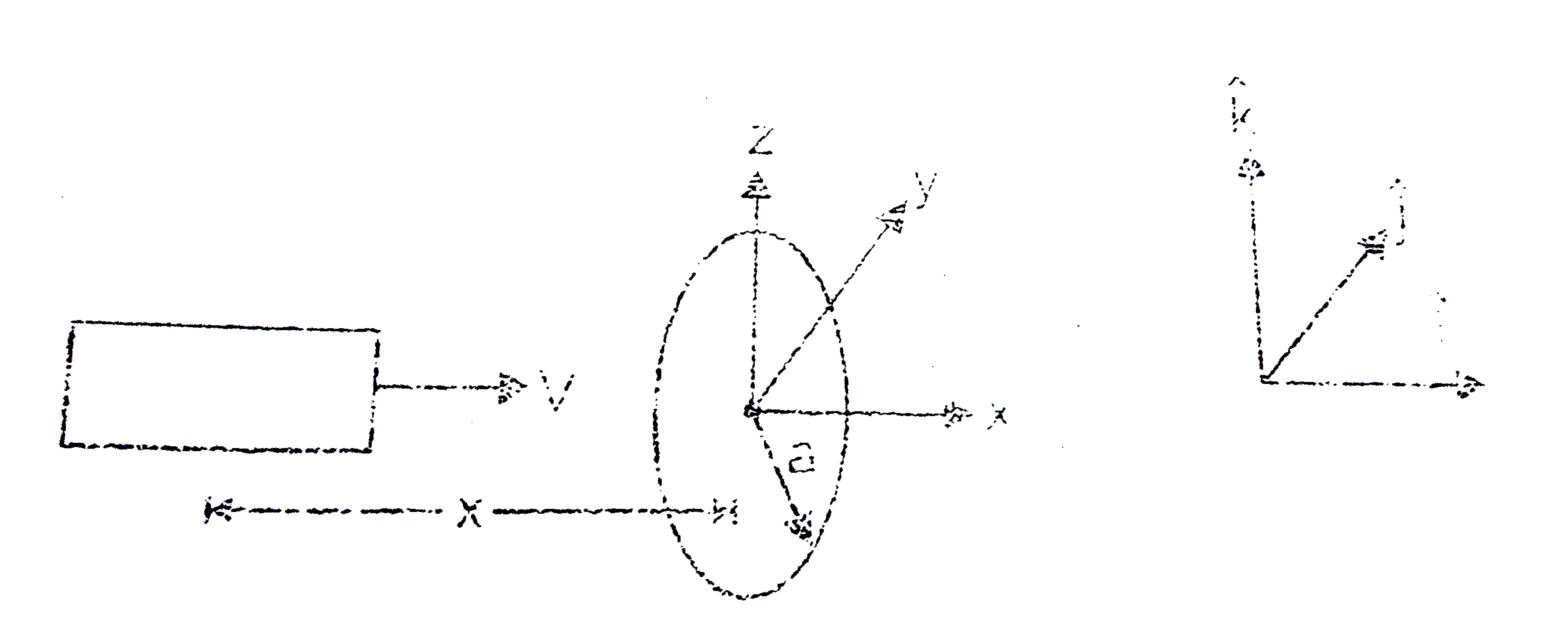
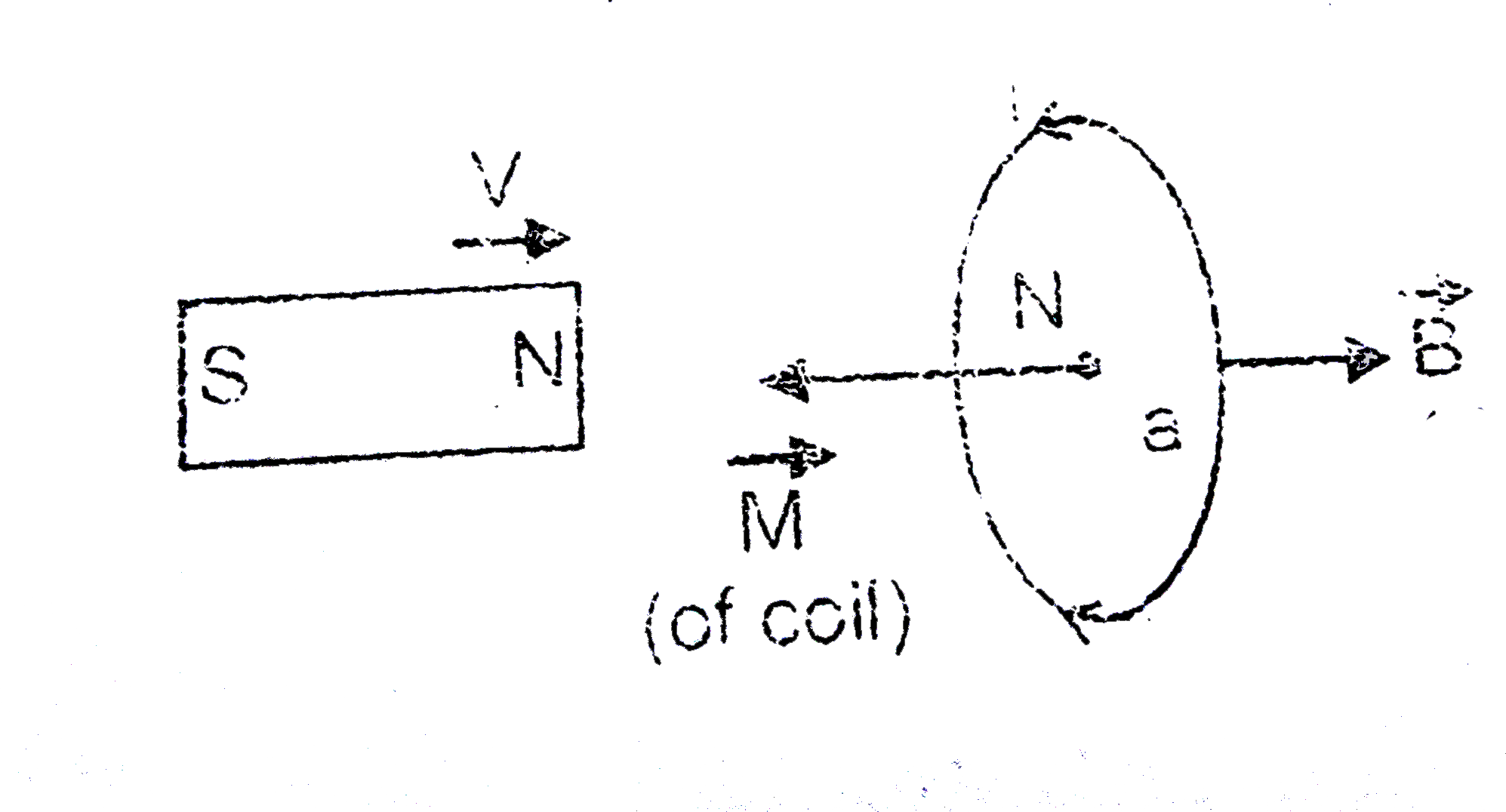
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercis-3 PART 3
Explore 16 Videos
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:Advanced level problems
Explore 31 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:HLP
Explore 40 Videos
Similar Questions
An infinitesimal bar magnet of dipole moment M is pointing and moving with speed v in the x-direction. A closed circular conducting loop of radius a and negligible self-inductance lies in the y−z plane with its centre at x=0 and its axis coinciding with x-axis. find the force opposing the motion of the magnet, if the resistance of the loop is R . Assume that the distance x of the magnet from the centre of the loop is much greater than a .
View SolutionThe dipole moment of a short bar magnet is 1.25A−m2. The magnetic field on its axis at a distance of 0.5 metre from the centre of the magnet is
View SolutionMagnetic moment of a square loop is M.What will be the magnetic moment of the loop if its shape is changed to circular
View SolutionThe magnetic field at a point x on the axis of a small bar magnet is equal to the field at a point y on the equator of the same magnet. The ratio of the distances of x and y from the centre of the magnet is
View SolutionA point lies on the x-axis. Find its y and z-cordinates
View SolutionA point lies on the x-axis. Find its y and z-cordinates
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.

View SolutionFigure shows a square loop 10cm on each side in the x−y plane with its centre at the origin. An infinite wire is at z=12cm above y-axis.
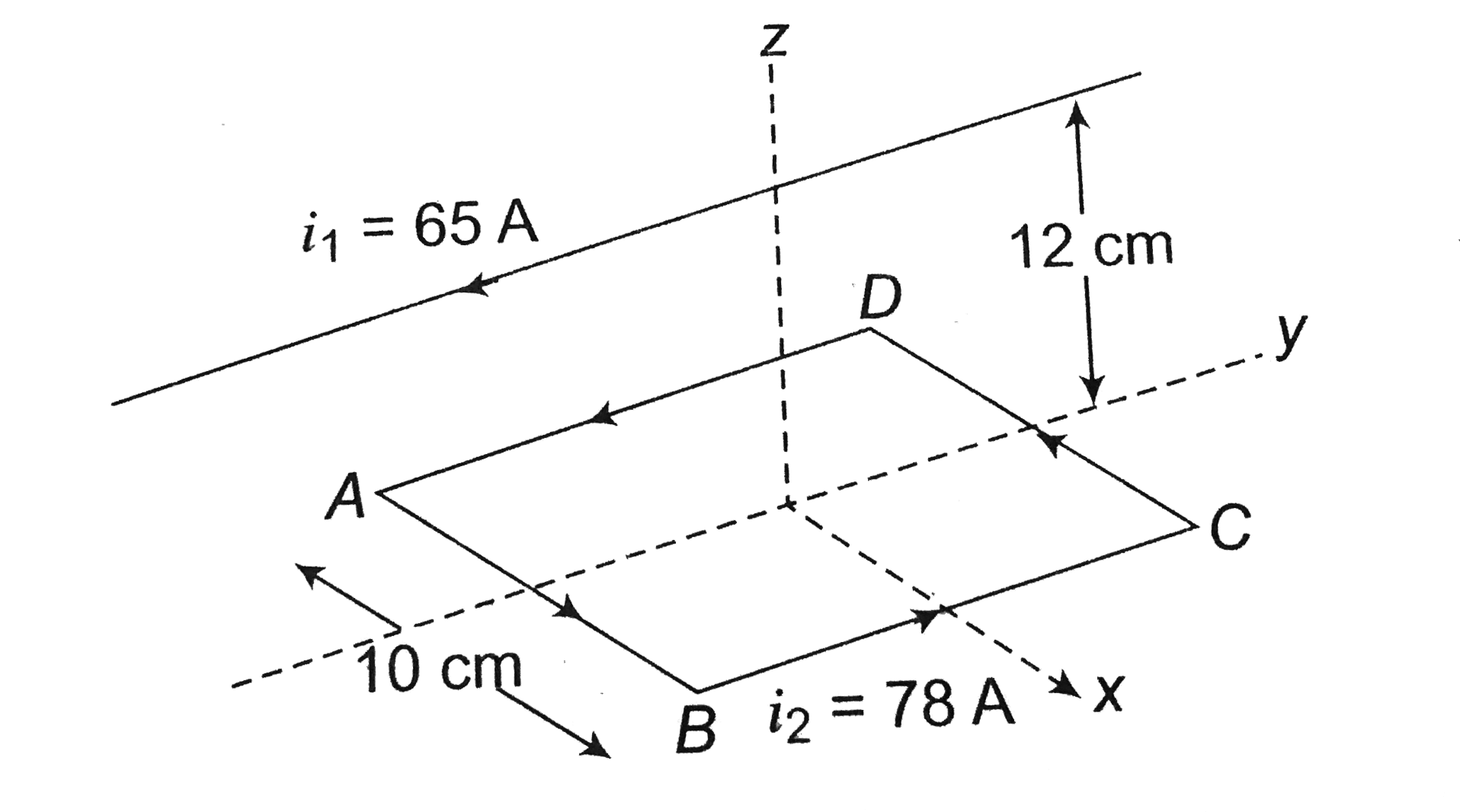 What is torque on loop due to magnetic force?
What is torque on loop due to magnetic force?
View Solution