In the above question find the force required to move the rod with constant velocity v, and also find the power delivered by the external agent.
To solve the problem of finding the force required to move the rod with constant velocity v and the power delivered by the external agent, we can follow these steps:
Step 1: Understand the setup
We have a conducting rod of length L moving with a constant velocity v in a magnetic field B. The motion of the rod in the magnetic field induces an electromotive force (emf) in the rod.
Step 2: Calculate the induced emf
The induced emf (E) in the rod can be calculated using the formula:
E=B⋅L⋅v
where B is the magnetic field strength, L is the length of the rod, and v is the velocity of the rod.
Step 3: Determine the current in the circuit
If the rod is part of a closed circuit with resistance R, the current I flowing through the circuit can be calculated using Ohm's law:
I=ER=B⋅L⋅vR
Step 4: Calculate the force required to move the rod
The force F required to move the rod with constant velocity can be determined using the formula:
F=B⋅I⋅L
Substituting the expression for I:
F=B⋅(B⋅L⋅vR)⋅L=B2⋅L2⋅vR
Step 5: Calculate the power delivered by the external agent
The power P delivered by the external agent can be calculated using the formula:
P=F⋅v
Substituting the expression for F:
P=(B2⋅L2⋅vR)⋅v=B2⋅L2⋅v2R
Summary of Results
- The force required to move the rod with constant velocity v is:
F=B2⋅L2⋅vR
- The power delivered by the external agent is:
P=B2⋅L2⋅v2R
We have a conducting rod of length L moving with a constant velocity v in a magnetic field B. The motion of the rod in the magnetic field induces an electromotive force (emf) in the rod.
The induced emf (E) in the rod can be calculated using the formula:
E=B⋅L⋅v
where B is the magnetic field strength, L is the length of the rod, and v is the velocity of the rod.
If the rod is part of a closed circuit with resistance R, the current I flowing through the circuit can be calculated using Ohm's law:
I=ER=B⋅L⋅vR
The force F required to move the rod with constant velocity can be determined using the formula:
F=B⋅I⋅L
Substituting the expression for I:
F=B⋅(B⋅L⋅vR)⋅L=B2⋅L2⋅vR
The power P delivered by the external agent can be calculated using the formula:
P=F⋅v
Substituting the expression for F:
P=(B2⋅L2⋅vR)⋅v=B2⋅L2⋅v2R
- The force required to move the rod with constant velocity v is:
F=B2⋅L2⋅vR
- The power delivered by the external agent is:
P=B2⋅L2⋅v2R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Problem
Explore 12 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercis-1
Explore 63 Videos
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:Advanced level problems
Explore 31 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:HLP
Explore 40 Videos
Similar Questions
In the block moves up with constant velocity v m/s. Find F

View SolutionIn the above question, the average power delivered by gravity is
View SolutionConsider a situation similar ot that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) what force is needed ot keep the rod sliding at a constant speed v? (b) in this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) find the power delivered by the external agent exerting the force on the rod.
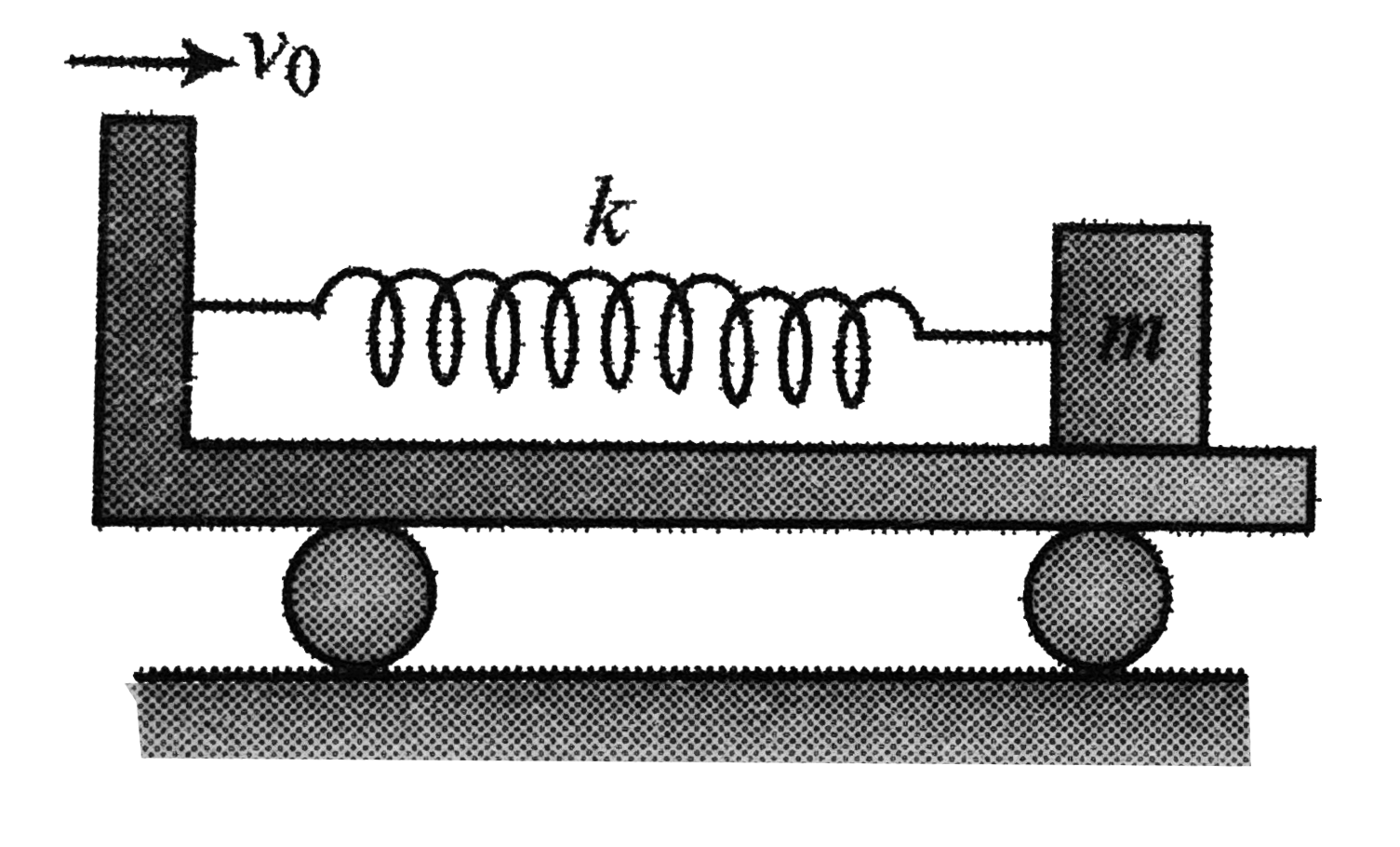
View SolutionA block of mass m is connected rigidly with a smooth wedge (plank) by a light spring of stiffness k. If the wedge is moved with constant velocity v0, find the work done by the external agent till the maximum compression of the spring.
View SolutionFig. Show a rectangular loop MNOP being pulled out of a magnetic field with a uniform velocity v by applying an external force F. The length MN is equal to l and the total resistance of the loop is R. Find(a) the current in the loop,(b) the magnetic force on the loop, (c) the external force F needed to maintain the velocity, (d) the power delivered by the external force and (e) the thermal power developed in the loop.

View SolutionA horizontal constant force F pulls a block of mass m placed on a horizontal surface. If the coefficient of kinetic friction between the block and ground is μ, find the power delivered by the external agent after a time agent after a time t measured from the beginning of action of the force.
View SolutionSand drops from a stationary hopper at the rate of 5kg/s on to a conveyor belt moving with a constant speed of 2m/s. What is the force required to keep the belt moving and what is the power delivered by the motor, moving the belt?
View SolutionA block of mass m is moving with a constant acceleration a on a rough horizontal plane. If the coefficient of friction between the block and ground is μ, the power delivered by the external agent in a time interval t from the beginning is equal to:
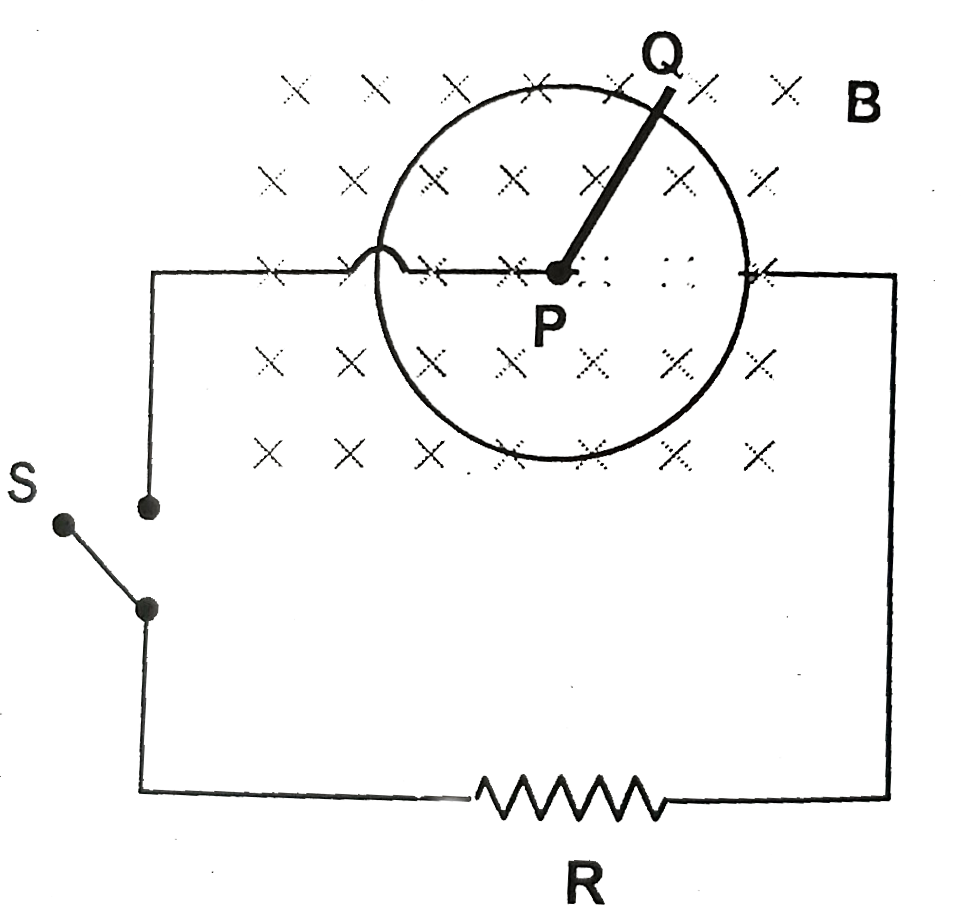
View SolutionA resitance R=1kΩ connected to a conducting rod PQ that can slide on a conducting circular ring of radius 2m with center at P. A constant uniform magnetic field 10 Tesla exist as shown in figure. At t=0, switch 'S' is closed and simulaneously an external torque is applied on the rod so that it rotates with constant angular velocity 20rad/sec. The magnitude of power delivered by external is 20K Watt. Find the value of K. (Neglect the gravity, friction and self inductance of circular loop)
View SolutionA power supply with an e.m.f ε and internal resustance r is connected to a variable resistance R. Find the dependence of the total power generated by the supply and of the power delivered to the external circuit on the load resistance.
View Solution

