A 1kg ball is suspended in a uniform electric field with the help of a string fixed to a point. The ball is given a charge √5 coulomb and the string makes an angle 37∘ with the vertical in equilibrium position. In the equilibrium position the tension is double the weight of the ball. Find the magnitude of the electric field in N/C.
The correct Answer is:6
To solve the problem, we need to analyze the forces acting on the charged ball in equilibrium and use the given information to find the magnitude of the electric field.
1. Identify the Forces Acting on the Ball:
- The weight of the ball (W) acting downwards: W=mg
- The tension (T) in the string acting at an angle of 37∘ with the vertical.
- The electric force (F_e) acting horizontally due to the electric field.
2. Given Information:
- Mass of the ball (m) = 1 kg
- Charge of the ball (Q) = √5 C
- Angle with the vertical = 37∘
- Tension (T) is double the weight of the ball: T=2W=2mg
3. Calculate the Weight of the Ball:
W=mg=1kg×10m/s2=10N
4. Calculate the Tension in the String:
T=2W=2×10N=20N
5. Resolve the Tension into Components:
- Vertical component of tension (T_y):
Ty=Tcos(37∘)=20cos(37∘)
- Horizontal component of tension (T_x):
Tx=Tsin(37∘)=20sin(37∘)
6. Using the Equilibrium Condition:
- In the vertical direction:
Ty=W⟹20cos(37∘)=10
- In the horizontal direction, the electric force (F_e) is equal to the horizontal component of tension:
Fe=Tx=20sin(37∘)
7. Calculate the Electric Force:
- Using sin(37∘)≈0.6:
Fe=20×0.6=12N
8. Relate Electric Force to Electric Field:
- The electric force is given by:
Fe=QE⟹E=FeQ
- Substituting the values:
E=12N√5C
9. Calculate the Magnitude of the Electric Field:
E=12√5≈122.236≈5.37N/C
Final Answer:
The magnitude of the electric field is approximately 5.37N/C.
- The weight of the ball (W) acting downwards: W=mg
- The tension (T) in the string acting at an angle of 37∘ with the vertical.
- The electric force (F_e) acting horizontally due to the electric field.
- Mass of the ball (m) = 1 kg
- Charge of the ball (Q) = √5 C
- Angle with the vertical = 37∘
- Tension (T) is double the weight of the ball: T=2W=2mg
W=mg=1kg×10m/s2=10N
T=2W=2×10N=20N
- Vertical component of tension (T_y):
Ty=Tcos(37∘)=20cos(37∘)
- Horizontal component of tension (T_x):
Tx=Tsin(37∘)=20sin(37∘)
- In the vertical direction:
Ty=W⟹20cos(37∘)=10
- In the horizontal direction, the electric force (F_e) is equal to the horizontal component of tension:
Fe=Tx=20sin(37∘)
- Using sin(37∘)≈0.6:
Fe=20×0.6=12N
- The electric force is given by:
Fe=QE⟹E=FeQ
- Substituting the values:
E=12N√5C
E=12√5≈122.236≈5.37N/C
The magnitude of the electric field is approximately 5.37N/C.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
A small ball is suspended by a string from the ceiling of a car. As the car accelerates at a rate ‘a’ the string makes an angle '/theta' with the vertical in equilibrium. Then the tension in the string is :
View SolutionA small metal ball is suspended in a uniform electric field with the help of an insulated thread. If high energy X-ray beam falls on the ball, the ball will be deflected in the direction of the field.
View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionA simple pendulum consists of a 50 cm long string connected to a 100 g ball. The ball is pulled aside so that the string makes an angel of 370 with the vertical and is then released. Find the tension in the string when the bob is at its lowest position.

View SolutionA ball of mass 1kg is suspended by an inextensible string 1m long attached to a point O of a smooth horizontal bar resting on fixed smooth supports A and B. The ball is released from rest from the position when the string makes an angle 30∘ with the vertical. The mass of the bar is 4kg. The displacement of bar when ball reaches the other extreme position (in m) is

View SolutionA bob of mass m suspended by a light inextensible string of length 'l' from a fixed point. The bob is given a speed of √6gl. Find the tension in the string when string deflects through an angle 120∘ from the vertical.
View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View SolutionA heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
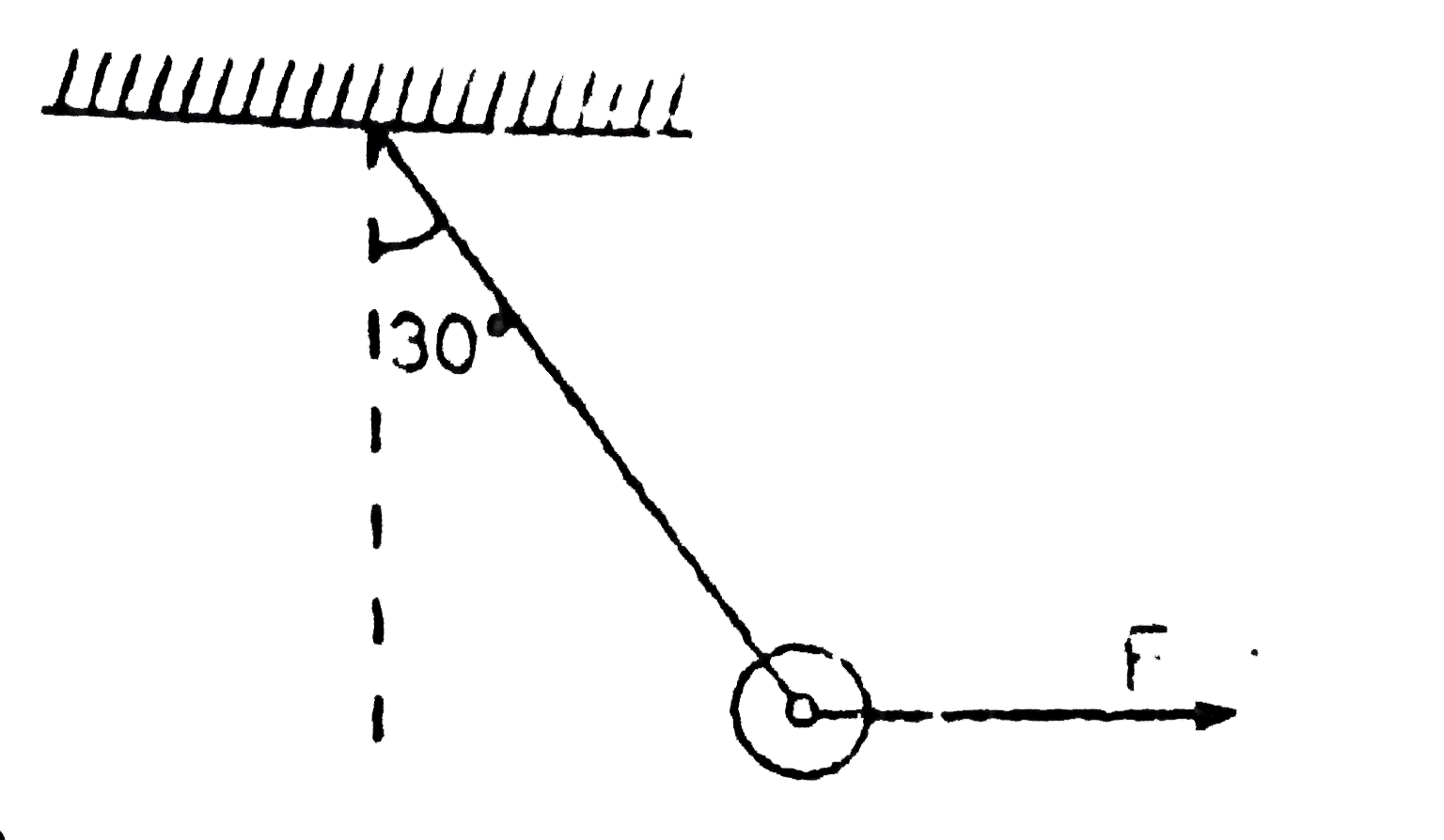 .
.
View SolutionOne end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and charge of 4×10−6C. In equilibrium, thread makes an angle of 60o with the vertical.
(a) Find the tension in the string in equilibrium.
(b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
(Use σ=7.5×10−7Cm2)
View SolutionA pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Find the angle made by the string with vertical at equilibrium. Also find the tension in the sting in this position

View Solution
