A small ball is suspended by a string from the ceiling of a car. As the car accelerates at a rate ‘a’ the string makes an angle '/theta' with the vertical in equilibrium. Then the tension in the string is :
m√a2+g2
ma√a2+g2
mgsinθ
mgcosθ
The correct Answer is:A
To find the tension in the string when a small ball is suspended from the ceiling of a car that is accelerating at a rate 'a', and the string makes an angle θ with the vertical, we can follow these steps:
1. Identify Forces Acting on the Ball:
- The ball experiences two main forces:
- The gravitational force (weight) acting downwards: Fg=mg
- The tension in the string acting at an angle θ from the vertical: T
2. Consider the Pseudo Force:
- Since the car is accelerating, we can consider a pseudo force acting on the ball in the opposite direction of the car's acceleration. This pseudo force is given by:
Fpseudo=ma
3. Draw the Free Body Diagram:
- In the frame of reference of the car, the ball is in equilibrium. The tension T can be resolved into two components:
- A vertical component: Tcosθ
- A horizontal component: Tsinθ
4. Set Up the Equilibrium Conditions:
- Since the ball is in equilibrium, the sum of forces in both the vertical and horizontal directions must be zero.
- In the vertical direction:
Tcosθ=mg (1)
- In the horizontal direction:
Tsinθ=ma (2)
5. Divide Equation (2) by Equation (1):
- To eliminate T, we can divide the horizontal force equation by the vertical force equation:
TsinθTcosθ=mamg
- This simplifies to:
tanθ=ag
6. Express Tension in Terms of a and g:
- From equation (1), we can express T:
T=mgcosθ(3)
- To find T in terms of a and g, we can use the relationship derived from the tangent:
cosθ=g√a2+g2(using the identity sin2θ+cos2θ=1)
- Substituting this into equation (3):
T=mgg√a2+g2=mg⋅√a2+g2g=m√a2+g2
7. Final Result:
- Therefore, the tension in the string is:
T=m√a2+g2
- The ball experiences two main forces:
- The gravitational force (weight) acting downwards: Fg=mg
- The tension in the string acting at an angle θ from the vertical: T
- Since the car is accelerating, we can consider a pseudo force acting on the ball in the opposite direction of the car's acceleration. This pseudo force is given by:
Fpseudo=ma
- In the frame of reference of the car, the ball is in equilibrium. The tension T can be resolved into two components:
- A vertical component: Tcosθ
- A horizontal component: Tsinθ
- Since the ball is in equilibrium, the sum of forces in both the vertical and horizontal directions must be zero.
- In the vertical direction:
Tcosθ=mg (1)
- In the horizontal direction:
Tsinθ=ma (2)
- To eliminate T, we can divide the horizontal force equation by the vertical force equation:
TsinθTcosθ=mamg
- This simplifies to:
tanθ=ag
- From equation (1), we can express T:
T=mgcosθ(3)
- To find T in terms of a and g, we can use the relationship derived from the tangent:
cosθ=g√a2+g2(using the identity sin2θ+cos2θ=1)
- Substituting this into equation (3):
T=mgg√a2+g2=mg⋅√a2+g2g=m√a2+g2
- Therefore, the tension in the string is:
T=m√a2+g2
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:LEVEL 2
Explore 49 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )
Explore 16 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:LEVEL 0 (LONG ANSWER TYPE)
Explore 4 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:JEE ADVANCED ARCHIVE
Explore 68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:IN-CHAPTER EXERCISE-G
Explore 10 Videos
Similar Questions
A mass 'M' is suspended by a rope from a rigid support. It is pulled horizontally with a force F. If the rope makes an angle ' θ' with vertical in equilibrium, then the tention in the string is
View SolutionA pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Find the angle made by the string with vertical at equilibrium. Also find the tension in the sting in this position

View SolutionA small sphere is suspended by a string from the ceiling of a car. If the car beings to move with a constant acceleration a, the inclination of the string to the vertical is:
View SolutionA mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
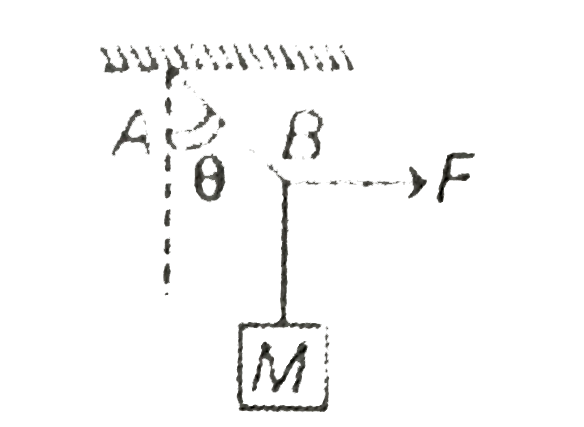
View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View SolutionA spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle θ with the vertical. The extension of the spring is.
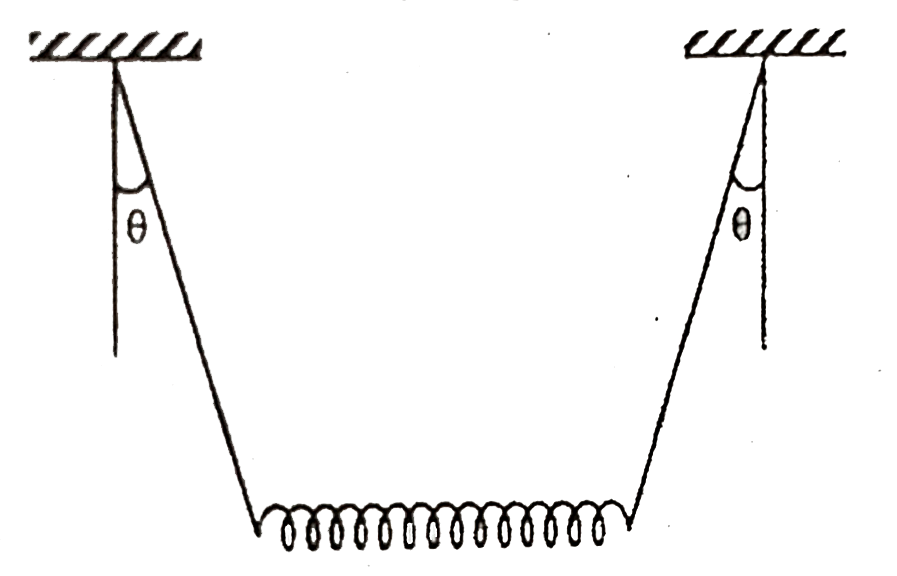
View SolutionA pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Find the angle made by the string with the vertical.
View SolutionA body of mass √3 kg is suspended by a string to a rigid support. The body is pulled horizontally by a force F until the string makes an angle of 30° with the vertical. The value of F and tension in the string are.
View SolutionA bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle 37∘ with the vertical. Find the acceleration of the trolley.

View Solution