A uniform electric field in positive x-direction on exists in space. An uncharged solid conducting sphere is now placed in region of this uniform electric field. The centre of this sphere of radius R lies at origin. Then electric potential at any point on y−z plane (i.e. x=0 plane) due to only induced charged on surface of sphere.
A. will be positive
B. will be negative
C. will be zero
D. may be positive, zero or negative
The correct Answer is:C
To find the electric potential at any point on the y-z plane (where x=0) due to the induced charges on the surface of an uncharged solid conducting sphere placed in a uniform electric field, we can follow these steps:
Step 1: Understand the Setup
We have a uniform electric field directed along the positive x-direction. When an uncharged conducting sphere is placed in this field, charges within the sphere will redistribute themselves due to the influence of the electric field.
Hint: Visualize the electric field lines and how they interact with the conducting sphere.
Step 2: Charge Redistribution
Due to the uniform electric field, positive charges will accumulate on the side of the sphere facing the direction of the electric field (the right side, in this case), while negative charges will accumulate on the opposite side (the left side). This creates a dipole-like charge distribution on the sphere.
Hint: Remember that conductors allow free movement of charges, which leads to this redistribution.
Step 3: Analyze the Electric Potential
The electric potential V at a point in space due to a charge distribution is given by the formula:
V=k∫dqr
where k is Coulomb's constant, dq is the charge element, and r is the distance from the charge element to the point where the potential is being calculated.
Hint: Consider the symmetry of the problem when calculating the potential.
Step 4: Consider the Y-Z Plane
In the y-z plane (where x=0), the induced charges on the sphere will create an electric potential. However, due to the symmetry of the charge distribution (equal positive and negative charges on opposite sides), the contributions to the potential from these charges will cancel out at any point in the y-z plane.
Hint: Think about how the potential due to a dipole behaves in relation to its axis.
Step 5: Conclusion
Since the potential due to the induced charges on the surface of the sphere cancels out at every point in the y-z plane, the electric potential at any point on the y-z plane is zero.
V=0for all points in the y-z plane
Final Answer: The electric potential at any point on the y-z plane due to the induced charges on the surface of the sphere is zero.
We have a uniform electric field directed along the positive x-direction. When an uncharged conducting sphere is placed in this field, charges within the sphere will redistribute themselves due to the influence of the electric field.
Due to the uniform electric field, positive charges will accumulate on the side of the sphere facing the direction of the electric field (the right side, in this case), while negative charges will accumulate on the opposite side (the left side). This creates a dipole-like charge distribution on the sphere.
The electric potential V at a point in space due to a charge distribution is given by the formula:
V=k∫dqr
where k is Coulomb's constant, dq is the charge element, and r is the distance from the charge element to the point where the potential is being calculated.
In the y-z plane (where x=0), the induced charges on the sphere will create an electric potential. However, due to the symmetry of the charge distribution (equal positive and negative charges on opposite sides), the contributions to the potential from these charges will cancel out at any point in the y-z plane.
Since the potential due to the induced charges on the surface of the sphere cancels out at every point in the y-z plane, the electric potential at any point on the y-z plane is zero.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
A hollow insulated conducting sphere is given a positive charge of 10μC . What will be the electric field at the centre of the sphere it is radius is 2 metres ?
View SolutionA metallic solid sphere is placed in a uniform electric field. The lines of force follow the path(s) shown in Figure as
View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionA solid metallic sphere is placed in a uniform electric field. Which of the lines A, B, C and D shows the correct path and why ?
View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is

View SolutionA point positive charge is brought near an isolated conducting sphere as shown in figure the electric field is best given by
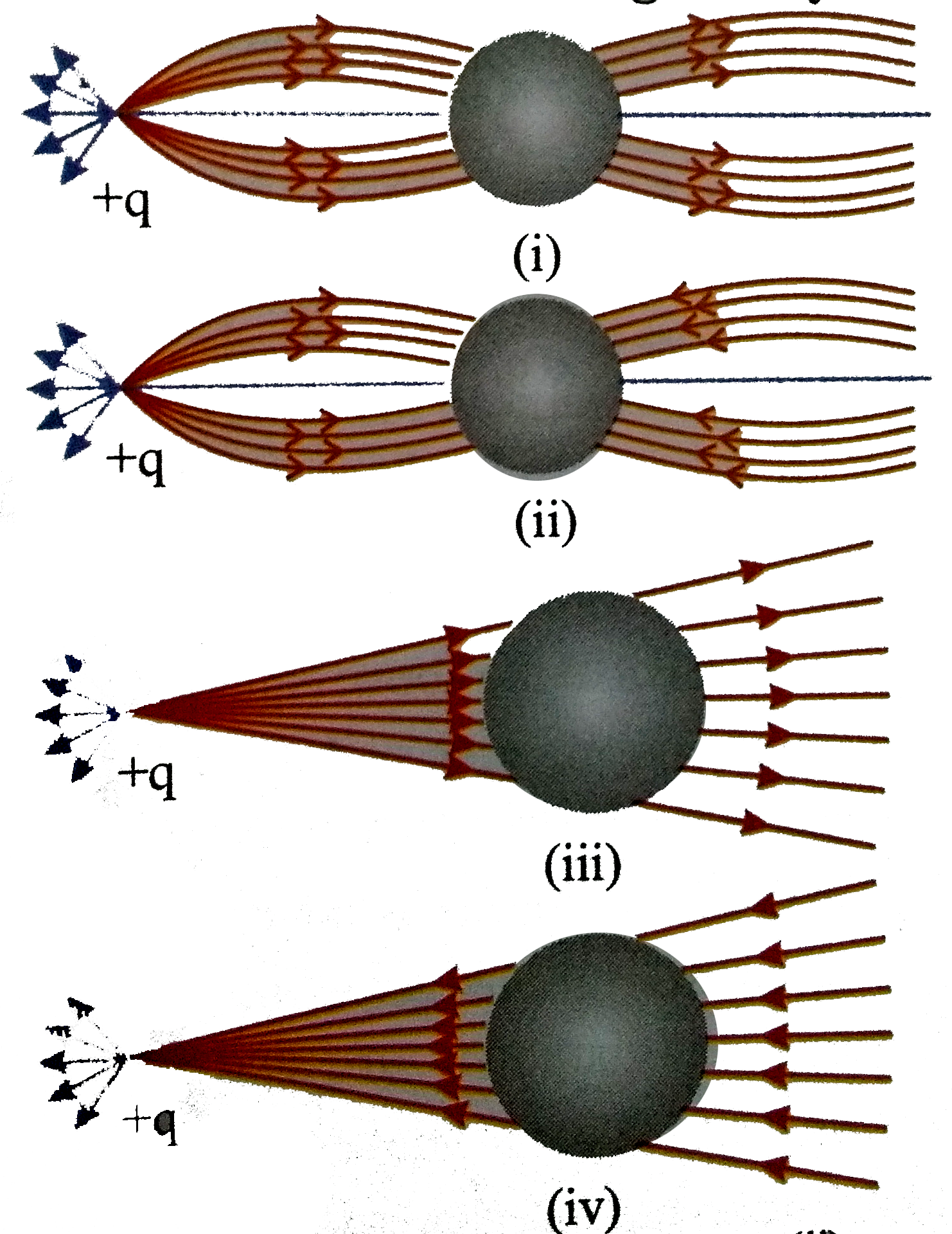
View SolutionA point positive charge is brought near an isolated conducting sphere. The electric field is best given by

View SolutionA point positive charge is brought near an isolated conducting sphere as shown in figure the electric field is best given by

View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View Solution
