Flux (ph) as a function of distance (r) from centre of uniformly charged solid sphere of charge Q and radius R, is best represented by
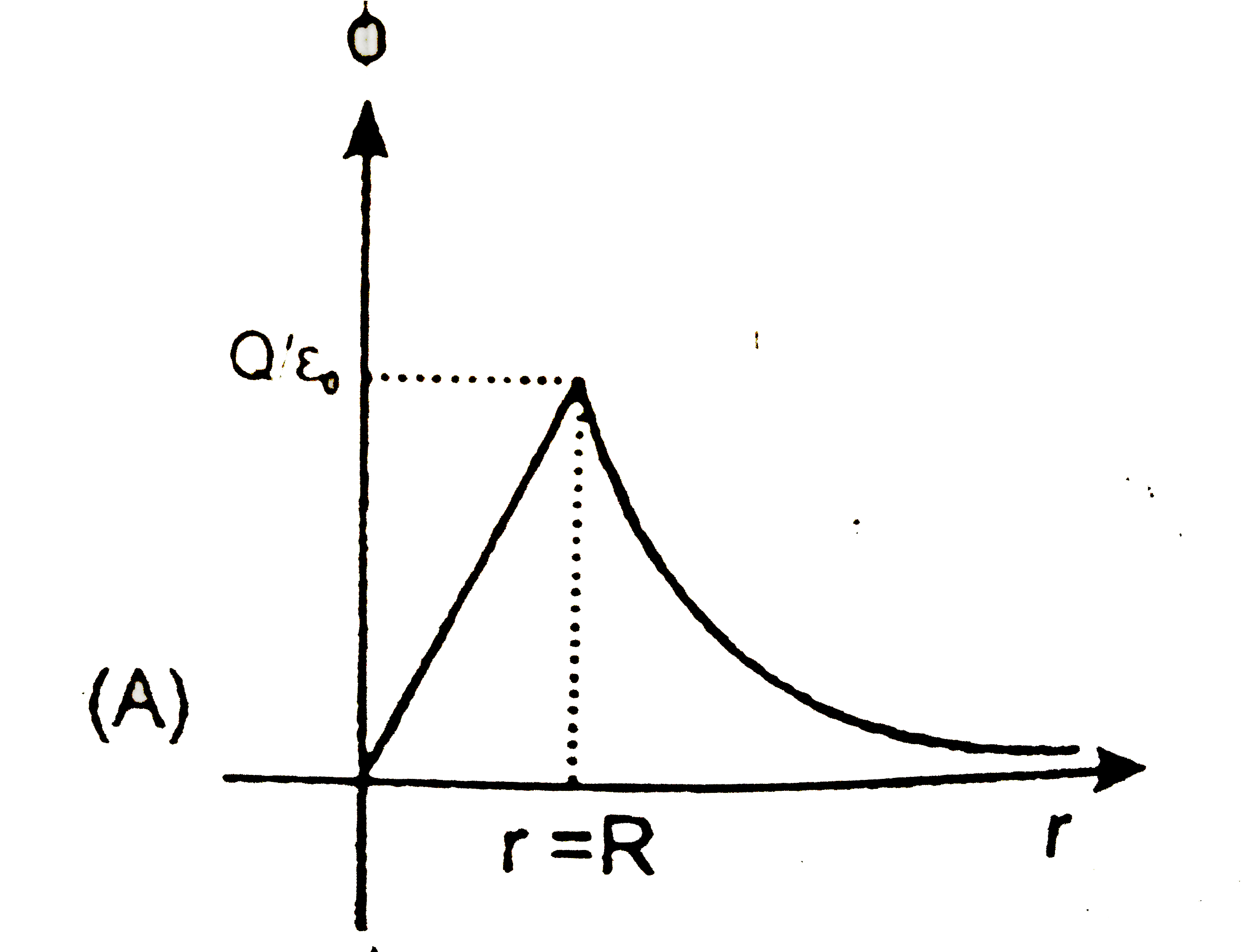
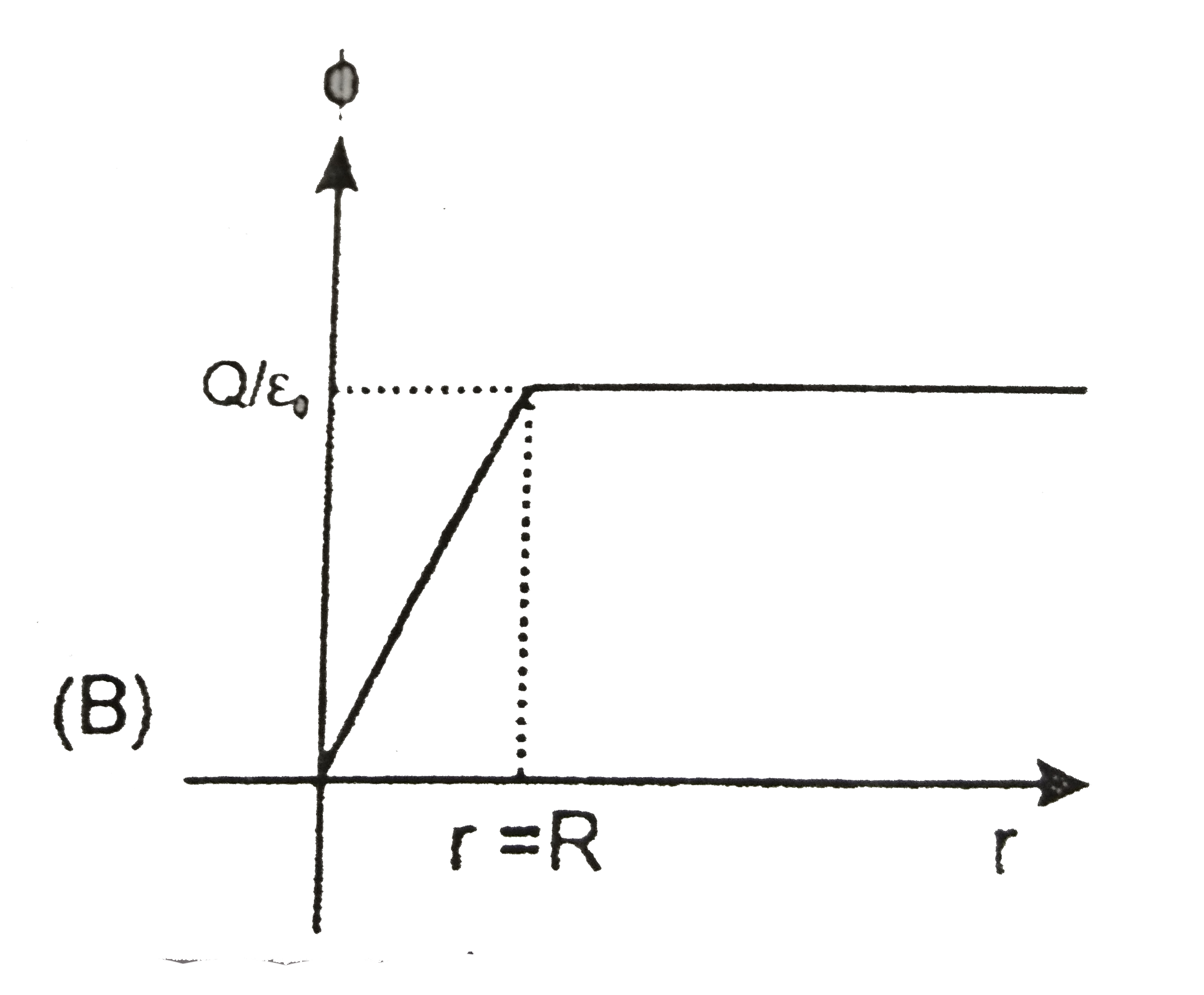
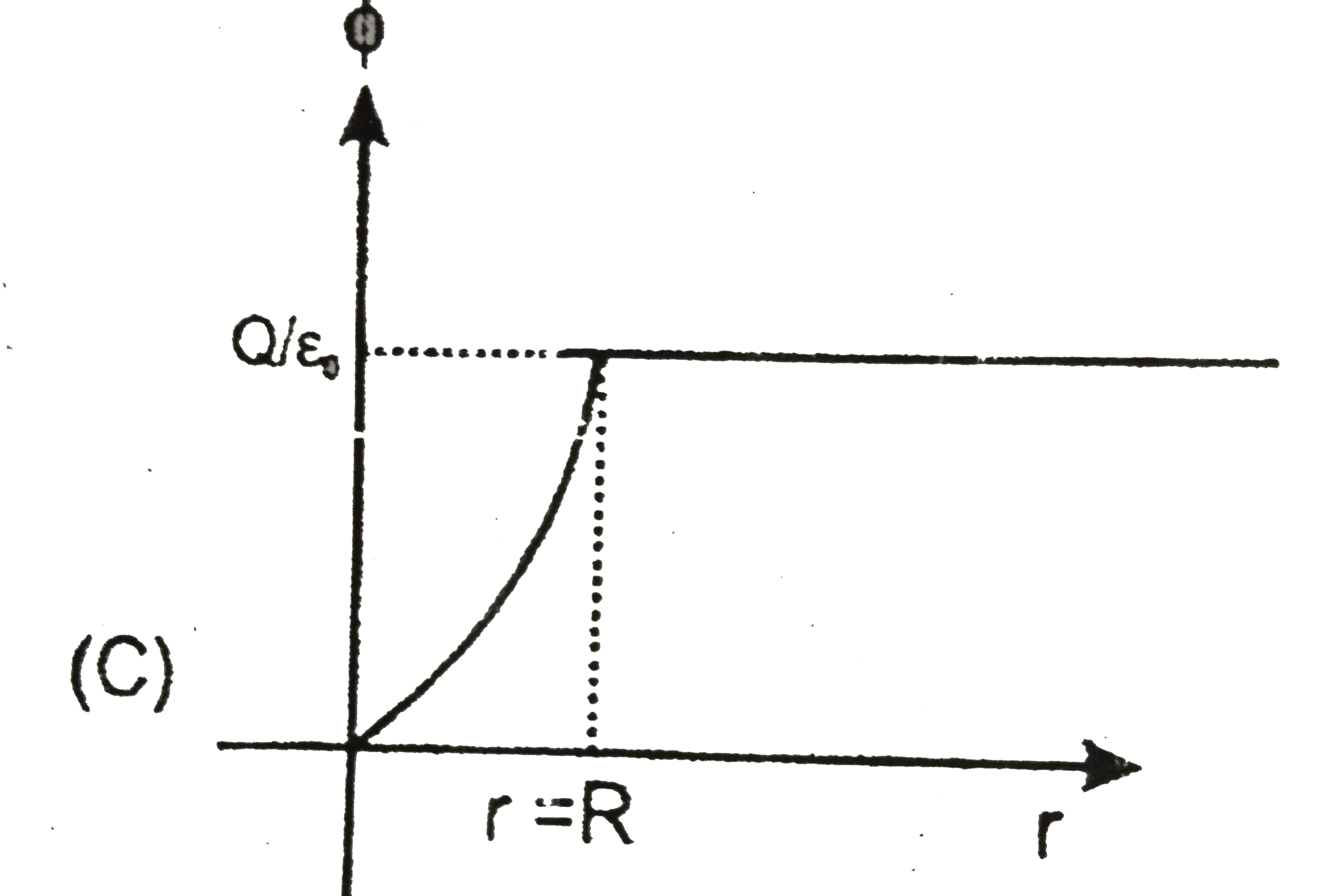
(D) 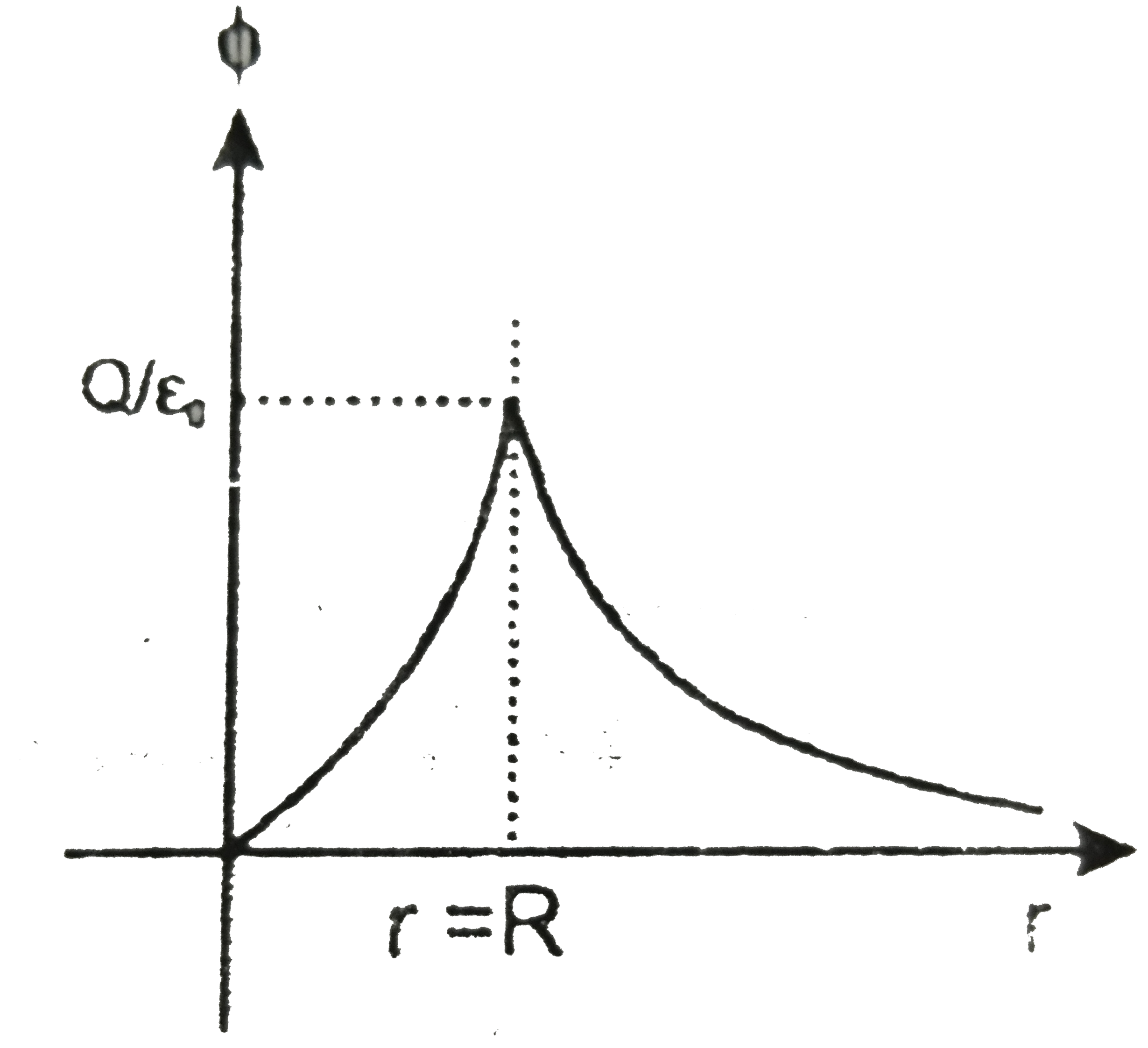
The correct Answer is:C
To find the relationship between the electric flux (Φ) and the distance (r) from the center of a uniformly charged solid sphere of charge Q and radius R, we can use Gauss's Law. Let's go through the solution step by step:
Step 1: Understanding Gauss's Law
Gauss's Law states that the electric flux through a closed surface is equal to the charge enclosed (Q_enc) divided by the permittivity of free space (ε₀):
Φ=Qencϵ0
Step 2: Case 1 - Inside the Sphere (r < R)
When we are inside the sphere (r < R), we need to find the charge enclosed (Q_enc) within a Gaussian surface of radius r.
1. The charge density (ρ) of the sphere can be calculated as:
ρ=Q43πR3
2. The volume of the Gaussian surface of radius r is:
V=43πr3
3. The charge enclosed (Q_enc) within this Gaussian surface is:
Qenc=ρ⋅V=⎛⎝Q43πR3⎞⎠⋅(43πr3)=Q⋅r3R3
4. Now, substituting Q_enc into Gauss's Law:
Φ=Q⋅r3R3ϵ0=Qϵ0⋅r3R3
This shows that the flux (Φ) is proportional to r3 when r<R.
Step 3: Case 2 - Outside the Sphere (r ≥ R)
When we are outside the sphere (r ≥ R), the entire charge Q is enclosed within the Gaussian surface.
1. The charge enclosed is simply Q.
2. Applying Gauss's Law:
Φ=Qϵ0
This indicates that the flux (Φ) is constant and does not depend on r when r≥R.
Step 4: Summary of Results
- For r<R: Φ∝r3
- For r≥R: Φ=Qϵ0 (constant)
Conclusion
The relationship between the electric flux and the distance from the center of the uniformly charged solid sphere is best represented by a graph that shows:
- A cubic relationship for r<R (increases as r3)
- A constant value for r≥R
Thus, the correct option is C.
---
Gauss's Law states that the electric flux through a closed surface is equal to the charge enclosed (Q_enc) divided by the permittivity of free space (ε₀):
Φ=Qencϵ0
When we are inside the sphere (r < R), we need to find the charge enclosed (Q_enc) within a Gaussian surface of radius r.
ρ=Q43πR3
2. The volume of the Gaussian surface of radius r is:
V=43πr3
Qenc=ρ⋅V=⎛⎝Q43πR3⎞⎠⋅(43πr3)=Q⋅r3R3
Φ=Q⋅r3R3ϵ0=Qϵ0⋅r3R3
This shows that the flux (Φ) is proportional to r3 when r<R.
When we are outside the sphere (r ≥ R), the entire charge Q is enclosed within the Gaussian surface.
2. Applying Gauss's Law:
Φ=Qϵ0
This indicates that the flux (Φ) is constant and does not depend on r when r≥R.
- For r<R: Φ∝r3
- For r≥R: Φ=Qϵ0 (constant)
The relationship between the electric flux and the distance from the center of the uniformly charged solid sphere is best represented by a graph that shows:
- A cubic relationship for r<R (increases as r3)
- A constant value for r≥R
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
Which graph best represents the variation of electric potential as a function of distance from the centre of a uniformly charged solid sphere of charge of radius R ?

View SolutionGraph shows magnitude of electric field (E), charge enclosed (qenclosed⟩) within the concentic sphere and net flux (ϕ) through a concentric spherical Gaussian surface as a function of distance (r) from centre of a uniformly positive charged solid sphere of radius R. Choose the correct option (s):
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionThe electric field intensity at a distance 20cm from the centre of a uniformly charged non conducting solid sphere of radius 10cm is E.Then what is the electric field intensity at a distance 5cm from the centre it will be.....
View SolutionA point charge of charge -q and mass m is released with negligible speed from a distance √3R on the axis of a fixed uniformly charged ring of charge Q and radius R. Find out its velocity when it reaches it reaches at the centre of the ring.

View SolutionVariation of electric potential due to npn-conducting (positively charged) solid sphere with distance from its centre is best represented as
View SolutionA point charge Q is situated (outside) at a distance r from the centre of an uncharged conducting solid sphere of radius R. The potential due to induced charges (on the conductor) at a point B inside the conductor whose distance form the point charge is d is ______
View SolutionA solid sphere of radius R is charged uniformly. The electrostatic potential V is plotted as a function of distance r from the centre of th sphere. Which of the following best represents the resulting curve?
View SolutionThe electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
View SolutionSTATEMENT 1: When a negative charge -q is released at a distance R from the centre and along the axis of a uniformly and positvely charged fixed ring of radius R, the negative charge does oscillation but not SHM. STATEMENT 2: The force on negative charge is always towards the centre of the ring but it is not proportional to the displacement from the centre of the ring.
View Solution
