A uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius R. Then the magnitude of gravitational force exerted by earth on the rod is 
GMm2R2
GMm4R2
4GMm9R2
GMm8R2
The correct Answer is:A
F=∫2RR=GM(mR)dxx2=GMm2R2 
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
A uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius is R. If the magnitude of gravitational force exerted by earth on the rod is ηGMm12R2 then η is
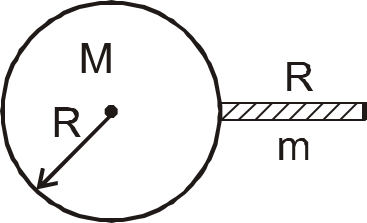
View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius is R. If the magnitude of gravitational force exerted by earth on the rod is ηGMm12R2 then η is

View Solution
Knowledge Check
If M is the mass of the earth and R its radius, then ratio of the gravitational acceleration and the gravitational constant is
AR2EMEBMER2ECMER2EDMEREA point mass m is placed inside a spherical shell of radius R and mass M at a distance R2 form the centre of the shell. The gravitational force exerted by the shell on the point mass is
AGMmR2B2GMmR2CzeroD4MmR2
If M is the mass of the earth and R its radius, the radio of the gravitational acceleration and the gravitational constant is
View SolutionGravitational potential energy of body of mass m at a height of h above the surface of earth (M = mass of earth , R = radius of earth) is
View SolutionA body of mass m is placed on the earth's surface . It is taken from the earth's surface to a height h = 3 R where R is the radius of the earth. The change in gravitational potential energy of the body is
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View SolutionThe acceleration due to gravity at a piece depends on the mass of the earth M, radius of the earth R and the gravitational constant G. Derive an expression for g?
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View Solution
